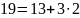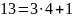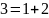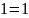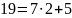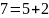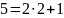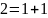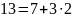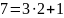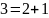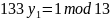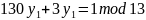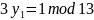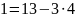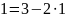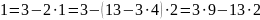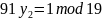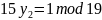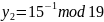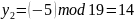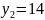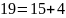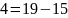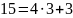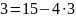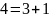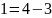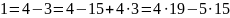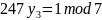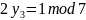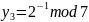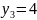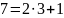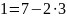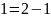Лабораторные и практики / 02_ЛР / 02_ЛР

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

_____________________________________________________________________________

Кафедра информационной безопасности телекоммуникационных систем

Дисциплина «Основы криптографии с открытыми ключами»

Лабораторная работа 2

«Основы теории чисел»

Выполнила: студ. гр. .

.

\

Проверил: проф. Яковлев В.А..

Санкт-Петербург

2021

Цель работы:

Закрепить знания, полученные на лекциях дисциплин «Основы криптографии», «Криптографические методы защиты информации» и приобрести навыки вычислений по блоку занятий «Математический базис криптосистем с открытым ключом».

Задание

1.Выполнить упражнения по определению делимости чисел, нахождению их наибольшего общего делителя (gcd(a,b)) и по нахождению канонического представления gcd и обратного элемента при помощи расширенного алгоритма Евклида.

2.Произвести определение конгруэнтности чисел, проверку утверждений теорем Эйлера и Ферма, убедиться в возможности быстрого вычисления возведения в степень и обращения чисел по модулю.

Ход работы:

1. Проверим, являются ли числа d делителями n, используя следующую команду: integerp(n/d), где n и d - произвольные пятиразрядные числа.

1. Выполнение команды integerp(n/d).

2. Найдем делители нескольких пятиразрядных чисел при помощи следующей команды: divisors(n)

2. Выполнение команды divisors(n).

Убедимся в правильности расчетов, посчитав “вручную” на примере первой функции.

Число 11111 делится на само себя и на 1, разделим число на 41 и 271.

11111		41			11111		271
_82		271			1084		41
291					271
287					271
41					0
41
0

Проверка проведена успешно, расчёт функции верен.

3. Для нескольких пар пяти разрядных чисел и одной пары четырех разрядных чисел используем команду: gcd(a,b) .

3. Выполнение команды gcd(a,b).

Убедимся в правильности расчетов “вручную”, выполнив следующее задание:

Найти наибольший общий делитель для пары чисел.

Четные номера. Найти НОД(8888,24NN),

Нечетные номера. Найти НОД(4848,12(NN+1)),

где NN –двузначный номер по журналу. Например, если номер 29, то второе число 1230.

Вариант №6.

НОД(8888, 2406)=?

Решение:

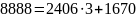
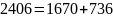
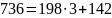
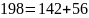
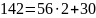
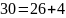
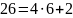
НОД: d=2

Результат: НОД(8888, 2406)=2.

4. Для найденных в п.3 пяти gcd(a,b), найдем их канонические представления при помощи расширенного алгоритма Евклида при помощи следующей команды: gcdex(a,b).

4. Выполнение команды gcdex(a,b).

Проверим правильность канонических представлений для всех случаев. Если функция отображает верный результат, то должно соблюдаться равенство (z1*a+z2*b)mod(b)= c, где z1, z2 - коэффициент перед большим числом a и коэффициент перед меньшим числом b соответственно, c равно НОД(a, b).

z1	z2	(z1*a+z2*b)mod(b)	c	Равенство
704	-153	(704*5678 - 15*1234)mod 5678=2	2	соблюдается
11	-2	(11 *67890 - 2*12345)mod 67890=15	15	соблюдается
19802	-3601	(19802 * 67891 - 3601*12346)mod 67891=1	1	соблюдается
-7714	1403	(1403 *12348 - 7714*67892)mod 67892=4	4	соблюдается
9319	-1695	(9319 * 67894 - 3601*12349)mod 67894=1	1	соблюдается

Проверка проведена успешно, программа сработала верно.

5. Для одного четырехразрядного числа и не менее чем для четырех произвольно выбранных пятизначных чисел a сделаем их приведение по модулям произвольных меньших чисел m при помощи команды: mod(a,m)

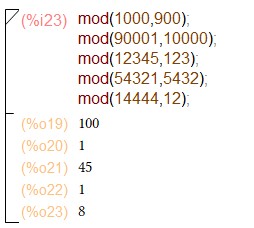
5. Выполнение команды mod(a,m).

Убедимся в правильности расчетов для чисел “вручную”.

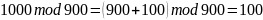
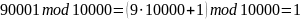
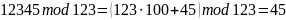
6. Найдем мультипликативно обратные элементы к одному двухразрядному числу и не менее чем к четырем девятизначным числам a по простым двузначным модулям m при помощи следующей команды:

power_mod(a,-1,m)

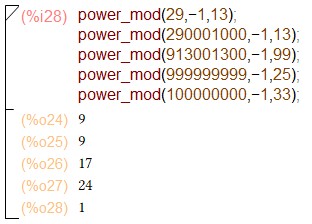
6. Выполнение команды power_mod(a,-1,m).

Убедимся в правильности расчетов “вручную”, выполнив следующее задание:

Найти обратный элемент к числу а по modb,

где a соответствует числу в таблице 1, порядковый номер которого совпадает с Вашим номером по журналу, b с номером большим на 10 порядковый номер числа а.

Например, если NN=29, то a=157 b=211

Таблица1.

23 29 31 37 41 43 47 53 59 61

67 71 73 79 83 89 97 101 103 107

Вариант №6.

a=43, b=89

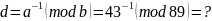
Решение:

Найдем обратный элемент





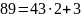
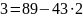
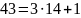
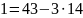
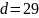
Проверка 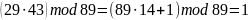, верно рассчитали

Результат:

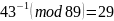
7. Рассчитаем функцию Эйлера для одного двухразрядного числа и не менее чем четырех четырехзначных чисел, используя команду: totient(m)

7. Выполнение команды totient(m).

Убедимся в правильности расчетов для первого числа “вручную”.

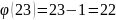
Проверка проведена успешно, расчёт функции верен.

8. Для двух пар произвольных четырехзначных, но взаимно простых чисел a и m, проверим справедливость теоремы Эйлера при помощи следующей команды: mod(a^ totient(m),m).

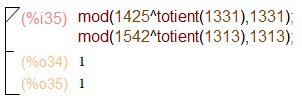
8. Выполнение команды mod(a^ totient(m),m).

9. Произведем возведение 5-значного произвольного числа a в степень произвольного 15-значного числа b по произвольному 4-х значному модулю m, используя команду: power_mod(a,b,m)

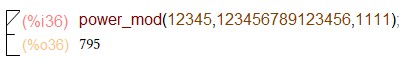
9. Выполнение команды divisors(n).

Убедимся, что возведение в степень выполняется быстрым алгоритмом, а не b–кратным перемножением числа a самого на себя с приведением по модулю, рассчитав примерное время вычислений на данном компьютере при использовании метода перемножения.

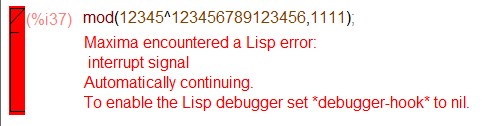
10. Перемножение числа a самого на себя, с приведением по модулю.

Данная команда была прервана спустя 15 минут расчётов.

Первым способом результат был получен в течении минуты, вторым способом результат не удалось получить в течении 15 минут. Таким образом, мы убедились, что ранее проводился расчет быстрым алгоритмом.

Используя алгоритм быстрого возведения в степень, вычислить вручную:

Четные номера. 3^1NN(mod7).

Нечетные номера. 5^1NN(mod7).

Например, если номер 3, то показатель степени 103.

Вариант №6.

Решение:

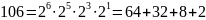
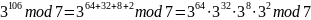
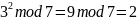
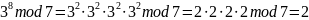
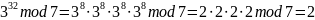
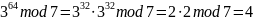
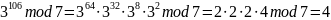
Результат: 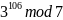=4.

10. Решить систему уравнений на основе использования китайской теоремы об остатках.

,

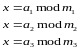где 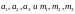заданы таблицей

№ вар	ai	mi
6	4,5,6	13,19,7

Решение:

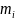и 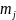взаимно простые числа:

НОД(13,19)=1	НОД(19,7)=1	НОД(7,13)=1

Тогда

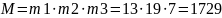
Найдем по формуле ,

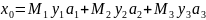где , .

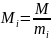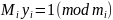Найдем , ,

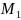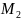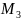
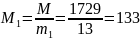
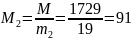
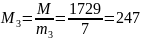
Найдем , ,

	 
	  
	 

, ,

, ,

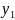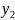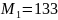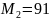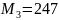
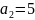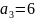, , , M = 1729

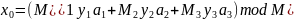
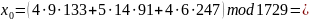
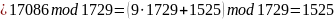
Ответ:

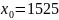
11. Решить контрольный пример.

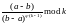, где

k=31,

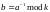
а=№вар+10.

Примечание. Если получаетcя b=а, положить b=25.

Вариант №6.

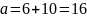
Решение:

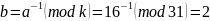
Ищем обратный элемент





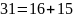
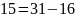
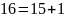
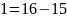
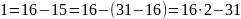
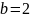
Проверка 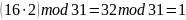, верно рассчитали

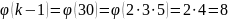
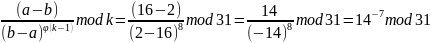
Ищем обратный элемент







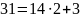
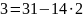
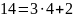
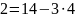
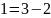
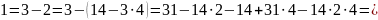
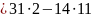
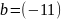
Проверка 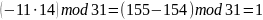, верно

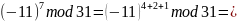
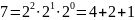
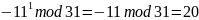
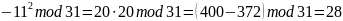
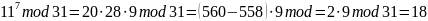
Результат:

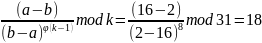
Вывод:

В ходе лабораторной работы мы закрепили знания, полученные на лекциях дисциплин «Основы криптографии», «Криптографические методы защиты информации» и приобрели навыки вычислений по блоку занятий «Математический базис криптосистем с открытым ключом».