
171100
.pdfМІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ “ЛЬВІВСЬКА ПОЛІТЕХНІКА”
РОЗКЛАД ДОВІЛЬНОЇ ФУНКЦІЇ В РЯД
ЗА СФЕРИЧНИМИ ФУНКЦІЯМИ
МЕТОДИЧНІ ВКАЗІВКИ
до виконання лабораторної роботи з курсу ”Основи фізичної геодезії” базового напряму 6.080101 “Геодезія, картографія та землеустрій”
Затверджено на засіданні кафедри
вищої геодезії та астрономії. Протокол № 10 від 15.05.2017 р.
Львів – 2017
Розклад довільної функції в ряд за сферичними функціями : метод.
вказівки до лабораторної роботи з курсу “Основи фізичної геодезії” для студентів геодезичних спеціальностей / уклад.: Б. Б. Джуман, О. М. Марченко. – Львів : Видавництво Львівської політехніки, 2017. – 12 с.
Укладачі |
Джуман Б. Б., канд. техн. наук, асист., |
|
Марченко О. М., д-р фіз.-мат. наук, проф. |
Відповідальний за випуск Заблоцький Ф. Д., д-р техн. наук, проф.
Рецензент Зазуляк П. М., д-р фіз.-мат. наук, проф.
2
Загальні положення
Починаючи з фундаментальних досліджень Лежандра і Гаусса в царині теорії ньютонівського потенціалу, класичним представленням гравітаційного поля або відповідного гравітаційного потенціалу небесних тіл став його запис у вигляді нескінчених рядів кульових функцій Лежандра, яке прийняло міждисциплінарне значення при вивченні статичних і залежних від часу полів Землі і планет. Варто зауважити, що така параметризація гравітаційного потенціалу не тільки вважається стандартною, але й однією з найкращих для розв’язування сучасних наукових і прикладних задач небесної механіки, супутникової геодезії, глобальної геодинаміки тощо [2].
Сферичні функції Лежандра можна отримати з розв’язку рівняння Лапласа
|
1 |
|
|
2 |
|
|
1 |
|
|
|
|
|
1 |
|
|
2 |
|
||||
|
|
|
r |
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
(1) |
|||
r2 |
|
|
|
|
|
|
r2 sin2 |
2 |
|||||||||||||
|
|
r |
|
r |
|
r2 sin |
|
|
|
||||||||||||
у сферичній системі координат. У рівнянні (1) |
|
|
– оператор Лапласа, r, , – |
||||||||||||||||||
сферичні координати.
Якщо ми спробуємо розв’язати рівняння Лапласа V = 0 в сферичних координатах методом розділення змінних за допомогою добутку трьох функцій, кожна з яких залежить тільки від однієї сферичної координати, отримаємо три диференційні рівняння другого порядку
r2 f (r) 2r f (r) n(n 1) f (r) 0 |
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
m |
|
|
|
||||
sin g ( ) cos g ( ) n(n 1)sin |
|
|
g( ) 0 |
. |
(2) |
||
sin |
|||||||
|
|
|
|
|
|||
|
|
|
|
|
|
||
h ( ) m2 h( ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Сферичні функції Лежандра є розв’язком двох останніх рівнянь (2), а
саме
g( ) Pnm (cos ) , |
(3а) |
h( ) cos m або h( ) sin m . |
(3б) |
Отже, шукані функції можна записати у вигляді
Rnm ( , ) Pnm (cos )cos(m ), |
(4) |
|
Snm ( , ) Pnm (cos )sin(m ). |
||
|
Геометрично сферичні функції можна представити так. Гармоніки з m=0 (поліноми Лежандра) мають n нулів. Усі ці нулі є дійсними і перебувають в інтервалі 1 cos 1, або, відповідно, 0≤ ≤π (рис. 1). отже, гармоніки при m=0 змінюють свій знак n разів на цьому інтервалі; крім того, вони не
3

залежать від λ. Їх геометричне представлення показано на рис. 1(а). Оскільки вони ділять сферу на зони, їх також називають зональними [1].
Приєднані функції Лежандра змінюють знак n-m разів на інтервалі 0≤ ≤π. Функції cosmλ і sinmλ мають 2m нулів на інтервалі 0≤λ≤2π, тож геометричне представлення гармонік при m≠0 показано на рис. 1(б). Вони ділять сферу на частини, в яких вони по черзі додатні і від’ємні, подібно до шахівниці, і називаються тесеральними гармоніками. Зокрема, при n=m, вони вироджуються в функції, які ділять сферу на додатні і від’ємні сектори, і в такому випадку їх називають секторіальними гармоніками (рис. 1(в)).
Рис. 1. Види сферичних функцій: (a) зональні, (б) тесеральні, (в) секторіальні [3]
4
Сферичні функції володіють властивістю ортогональності
|
|
|
|
Rnm ( , )Rsr ( , )d 0 |
|
||
|
|
|
якщо s n або r m; |
|
Snm ( , )Ssr ( , )d 0 |
|
|
|
(5) |
||
|
|
|
|
|
|
|
|
Rnm ( , )Ssr ( , )d 0 |
|
вбудь якомувипадку, |
|
|
|
|
|
а також їх можна нормувати
|
|
|
n0 ( , ) |
2n 1Rn0 |
( , ) |
2n 1Pn (cos ); |
|
|
|||||||
R |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
(n m)! |
|
|
|
|
|
|
|
Rnm ( , ) |
2(2n 1) |
Rnm ( , ) |
|
|
(6) |
||||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
(n m)! |
|
|
(m |
0). |
|||
|
|
|
|
|
|
|
|
(n m)! |
|
|
|
|
|
||
|
|
|
|
( , ) |
2(2n 1) |
|
S |
|
( , ) |
|
|
|
|||
S |
nm |
nm |
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
(n m)! |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Практично будь-яку функцію на сфері можна розкласти в ряд за сферичними функціями
n |
|
f ( , ) anmRnm ( , ) bnmSnm ( , ) , |
(7) |
n 0 m 0
де anm і bnm – невідомі коефіцієнти.
На практиці під час розкладу за сферичними функціями обмежуються певним максимальним порядком моделі Km , при чому кількість невідомих
коефіцієнтів можна знайти як (K m 1)2 .
Приклад обчислення моделі за сферичними функціями Лежандра
Вхідні дані:
θ |
λ |
f |
35° |
0° |
0.06747 |
35° |
90° |
0.02192 |
35° |
180° |
-0.06747 |
35° |
270° |
-0.02192 |
70° |
0° |
0.16726 |
70° |
90° |
0.05435 |
70° |
180° |
-0.16726 |
70° |
270° |
-0.05435 |
110° |
0° |
0.10491 |
110° |
90° |
0.03409 |
5
|
|
Продовження |
|
|
|
|
|
θ |
λ |
|
f |
110° |
180° |
|
-0.10491 |
110° |
270° |
|
-0.03409 |
145° |
0° |
|
0.01023 |
145° |
90° |
|
0.00332 |
145° |
180° |
|
-0.01023 |
145° |
270° |
|
-0.00332 |
Для побудови моделі fm за сферичними функціями слід обмежитись третім порядком
3 n |
|
fm ( , ) anmRnm ( , ) bnmSnm ( , ) . |
(8) |
n 0 m 0
У такому випадку кількість невідомих коефіцієнтів збігатиметься з кількістю рівнянь.
Аналітичний вигляд приєднаних сферичних функцій до 3-го порядку
такий: P 1, |
P |
cos , |
P |
|
sin , |
P |
|
1 (3cos |
2 1) , |
P |
3sin cos , |
||||
|
00 |
10 |
|
|
|
11 |
|
20 |
|
2 |
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
3sin2 , |
P |
1 (5cos3 3cos ) , |
|
|
P 3 sin (5cos2 1) , |
|||||||||
22 |
|
|
30 |
|
2 |
|
|
|
|
|
|
31 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P |
15sin2 cos , |
P |
|
15sin3 |
. |
|
|
|
|
|
|
|
|||
32 |
|
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
Складемо систему лінійних алгебраїчних рівнянь (СЛАР)
3 n |
|
fi\ anmRnm ( i , i ) bnmSnm ( i , i ) . |
(9) |
n 0 m 0
В СЛАР (9) 16 рівнянь і 16 невідомих, тому вона має єдиний розв’язок. Її можна подати в матричному вигляді як
AX L , |
(10) |
де вектор L складається із значень функції f, що містяться у вхідних даних, матриця А залежить лише від конфігурації заданих точок, а вектор Х – вектор невідомих коефіцієнтів anm і bnm.
Оскільки використовуються ненормовані сферичні функції, розв’язок (10) буде нестійким, тому його слід стабілізувати, ввівши параметр регуляризації Тихонова α так:
X ( AT A I ) 1( AT L) . |
(11) |
6 |
|

Матриця А в цьому випадку має вигляд
1,000 |
0,819 |
0,565 |
0,100 |
0,507 |
1,388 |
0,245 |
0,927 |
0,338 |
0,145 |
1,995 |
0,352 |
3,799 |
1,383 |
2,451 |
1,415 |
1,000 |
0,819 |
-0,100 |
0,565 |
0,507 |
-0,245 |
1,388 |
-0,927 |
-0,338 |
0,145 |
-0,352 |
1,995 |
-3,799 |
-1,383 |
1,415 |
-2,451 |
1,000 |
0,819 |
-0,565 |
-0,100 |
0,507 |
-1,388 |
-0,245 |
0,927 |
0,338 |
0,145 |
-1,995 |
-0,352 |
3,799 |
1,383 |
-2,451 |
-1,415 |
1,000 |
0,819 |
0,100 |
-0,565 |
0,507 |
0,245 |
-1,388 |
-0,927 |
-0,338 |
0,145 |
0,352 |
-1,995 -3,799 -1,383 |
-1,415 |
2,451 |
||
1,000 |
0,342 |
0,925 |
0,163 |
-0,325 |
0,950 |
0,167 |
2,489 |
0,906 |
-0,413 |
-0,576 |
-0,102 |
4,257 |
1,549 |
10,779 |
6,223 |
1,000 |
0,342 |
-0,163 |
0,925 |
-0,325 |
-0,167 |
0,950 |
-2,489 |
-0,906 -0,413 0,102 -0,576 -4,257 -1,549 |
6,223 |
-10,779 |
|||||
1,000 |
0,342 |
-0,925 |
-0,163 -0,325 -0,950 |
-0,167 |
2,489 |
0,906 |
-0,413 |
0,576 |
0,102 |
4,257 |
1,549 |
-10,779 |
-6,223 |
||
1,000 |
0,342 |
0,163 |
-0,925 -0,325 0,167 |
-0,950 |
-2,489 |
-0,906 -0,413 -0,102 0,576 -4,257 -1,549 |
-6,223 |
10,779 |
|||||||
1,000 |
-0,342 |
0,925 |
0,163 |
-0,325 |
-0,950 |
-0,167 |
2,489 |
0,906 |
0,413 |
-0,576 |
-0,102 -4,257 -1,549 |
10,779 |
6,223 |
||
1,000 |
-0,342 |
-0,163 |
0,925 |
-0,325 |
0,167 |
-0,950 |
-2,489 |
-0,906 0,413 0,102 -0,576 4,257 1,549 |
6,223 |
-10,779 |
|||||
1,000 |
-0,342 |
-0,925 |
-0,163 -0,325 0,950 |
0,167 |
2,489 |
0,906 |
0,413 |
0,576 |
0,102 |
-4,257 |
-1,549 |
-10,779 |
-6,223 |
||
1,000 |
-0,342 |
0,163 |
-0,925 -0,325 -0,167 |
0,950 |
-2,489 |
-0,906 0,413 -0,102 0,576 4,257 1,549 |
-6,223 |
10,779 |
|||||||
1,000 |
-0,819 |
0,565 |
0,100 |
0,507 |
-1,388 |
-0,245 |
0,927 |
0,338 |
-0,145 |
1,995 |
0,352 |
-3,799 |
-1,383 |
2,451 |
1,415 |
1,000 |
-0,819 |
-0,100 |
0,565 |
0,507 |
0,245 |
-1,388 |
-0,927 |
-0,338 |
-0,145 |
-0,352 |
1,995 |
3,799 |
1,383 |
1,415 |
-2,451 |
1,000 |
-0,819 |
-0,565 |
-0,100 |
0,507 |
1,388 |
0,245 |
0,927 |
0,338 |
-0,145 -1,995 -0,352 -3,799 -1,383 |
-2,451 |
-1,415 |
||||
1,000 |
-0,819 |
0,100 |
-0,565 |
0,507 |
-0,245 |
1,388 |
-0,927 |
-0,338 |
-0,145 |
0,352 |
-1,995 |
3,799 |
1,383 |
-1,415 |
2,451 |
Параметр регуляризації рекомендовано прийняти α = 0.0000001. Вектор невідомих коефіцієнтів дорівнює
-5,87 |
1,73 |
1,38 |
7,33E |
1,44 |
2,24 |
1,19 |
1,59 |
-4,37 |
-2,31 |
3,17 |
1,68 |
-2,40 |
6,61 |
1,13 |
2,40 |
|
E-18 |
E-17 |
E-03 |
-04 |
E-17 |
E-02 |
E-02 |
E-10 |
E-10 |
E-17 |
E-03 |
E-03 |
E-10 |
E-10 |
E-02 |
E-03 |
|
|
Оскільки параметр регуляризації спотворив розв'язок, необхідно знайти |
|||||||||||||||
відхилення моделі від вхідних даних |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
V AX L . |
|
|
|
|
|
|
|
(12) |
|||
На рис. 1 зображено вхідні дані L, модельні значення AX, а також їхні різниці V.
7
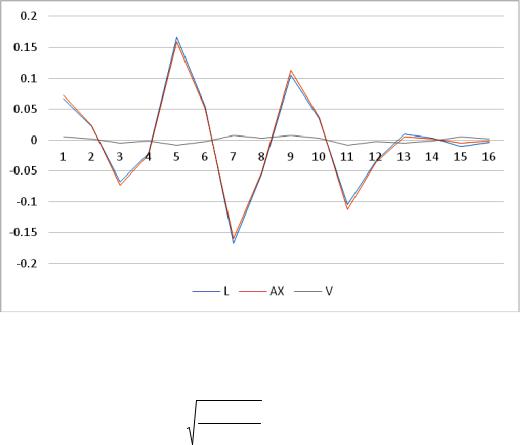
Рис. 1. Вхідні дані L, модельні значення AX та їх різниці V
Середню квадратичну похибку моделі m обчислюють за формулою
|
V T V |
|
m |
(K m 1)2 . |
(13) |
У цьому випадку m = 0,005.
Література
1.Марченко О. М. Дослідження гравітаційного поля, топографії океану та рухів земної кори в регіоні Антарктики: монографія / О. М. Марченко, К. Р. Третяк, А. Я. Кульчицький, Ю. І. Голубінка, Д. О. Марченко, Н. П. Третяк – Львів: Видавництво Львівської політехніки, 2012. – 308 с.
2.Джуман Б. Б. Про побудову моделі локального гравітаційного поля /
Б. Б. Джуман // Геодинаміка. – 2013. – № 1(14). – C. 29–33.
3.Режим доступу: http://icgem.gfz-potsdam.de/vis3d/tutorial
8

Вхідні дані
|
Варіант № 1 |
|
|
Варіант № 2 |
|
|
Варіант № 3 |
|
|
Варіант № 4 |
|||||||
35 |
|
20 |
0,06410 |
|
35 |
|
25 |
0,05448 |
|
35 |
30 |
0,04245 |
|
35 |
|
35 |
0,03013 |
35 |
|
110 |
0,05682 |
|
35 |
|
115 |
0,07969 |
|
35 |
120 |
0,10387 |
|
35 |
|
125 |
0,12687 |
35 |
|
200 |
-0,06410 |
|
35 |
|
205 |
-0,05448 |
|
35 |
210 |
-0,04245 |
|
35 |
|
215 |
-0,03013 |
35 |
|
290 |
-0,05682 |
|
35 |
|
295 |
-0,07969 |
|
35 |
300 |
-0,10387 |
|
35 |
|
305 |
-0,12687 |
70 |
|
20 |
0,15890 |
|
70 |
|
25 |
0,13505 |
|
70 |
30 |
0,10524 |
|
70 |
|
35 |
0,07469 |
70 |
|
110 |
0,14087 |
|
70 |
|
115 |
0,19755 |
|
70 |
120 |
0,25752 |
|
70 |
|
125 |
0,31454 |
70 |
|
200 |
-0,15890 |
|
70 |
|
205 |
-0,13505 |
|
70 |
210 |
-0,10524 |
|
70 |
|
215 |
-0,07469 |
70 |
|
290 |
-0,14087 |
|
70 |
|
295 |
-0,19755 |
|
70 |
300 |
-0,25752 |
|
70 |
|
305 |
-0,31454 |
110 |
|
20 |
0,09967 |
|
110 |
|
25 |
0,08471 |
|
110 |
30 |
0,06601 |
|
110 |
|
35 |
0,04685 |
110 |
|
110 |
0,08836 |
|
110 |
|
115 |
0,12392 |
|
110 |
120 |
0,16153 |
|
110 |
|
125 |
0,19730 |
110 |
|
200 |
-0,09967 |
|
110 |
|
205 |
-0,08471 |
|
110 |
210 |
-0,06601 |
|
110 |
|
215 |
-0,04685 |
110 |
|
290 |
-0,08836 |
|
110 |
|
295 |
-0,12392 |
|
110 |
300 |
-0,16153 |
|
110 |
|
305 |
-0,19730 |
145 |
|
20 |
0,00972 |
|
145 |
|
25 |
0,00826 |
|
145 |
30 |
0,00644 |
|
145 |
|
35 |
0,00457 |
145 |
|
110 |
0,00862 |
|
145 |
|
115 |
0,01208 |
|
145 |
120 |
0,01575 |
|
145 |
|
125 |
0,01924 |
145 |
|
200 |
-0,00972 |
|
145 |
|
205 |
-0,00826 |
|
145 |
210 |
-0,00644 |
|
145 |
|
215 |
-0,00457 |
145 |
|
290 |
-0,00862 |
|
145 |
|
295 |
-0,01208 |
|
145 |
300 |
-0,01575 |
|
145 |
|
305 |
-0,01924 |
|
Варіант № 5 |
|
|
Варіант № 6 |
|
|
Варіант № 7 |
|
|
Варіант № 8 |
||||
35 |
40 |
0,01920 |
|
35 |
45 |
0,01070 |
|
35 |
50 |
0,00499 |
|
35 |
55 |
0,00178 |
35 |
130 |
0,14592 |
|
35 |
135 |
0,15838 |
|
35 |
140 |
0,16219 |
|
35 |
145 |
0,15621 |
35 |
220 |
-0,01920 |
|
35 |
225 |
-0,01070 |
|
35 |
230 |
-0,00499 |
|
35 |
235 |
-0,00178 |
35 |
310 |
-0,14592 |
|
35 |
315 |
-0,15838 |
|
35 |
320 |
-0,16219 |
|
35 |
325 |
-0,15621 |
70 |
40 |
0,04759 |
|
70 |
45 |
0,02653 |
|
70 |
50 |
0,01236 |
|
70 |
55 |
0,00441 |
70 |
130 |
0,36175 |
|
70 |
135 |
0,39263 |
|
70 |
140 |
0,40209 |
|
70 |
145 |
0,38725 |
70 |
220 |
-0,04759 |
|
70 |
225 |
-0,02653 |
|
70 |
230 |
-0,01236 |
|
70 |
235 |
-0,00441 |
70 |
310 |
-0,36175 |
|
70 |
315 |
-0,39263 |
|
70 |
320 |
-0,40209 |
|
70 |
325 |
-0,38725 |
110 |
40 |
0,02985 |
|
110 |
45 |
0,01664 |
|
110 |
50 |
0,00775 |
|
110 |
55 |
0,00277 |
110 |
130 |
0,22691 |
|
110 |
135 |
0,24628 |
|
110 |
140 |
0,25221 |
|
110 |
145 |
0,24291 |
110 |
220 |
-0,02985 |
|
110 |
225 |
-0,01664 |
|
110 |
230 |
-0,00775 |
|
110 |
235 |
-0,00277 |
110 |
310 |
-0,22691 |
|
110 |
315 |
-0,24628 |
|
110 |
320 |
-0,25221 |
|
110 |
325 |
-0,24291 |
145 |
40 |
0,00291 |
|
145 |
45 |
0,00162 |
|
145 |
50 |
0,00076 |
|
145 |
55 |
0,00027 |
145 |
130 |
0,02213 |
|
145 |
135 |
0,02402 |
|
145 |
140 |
0,02460 |
|
145 |
145 |
0,02369 |
145 |
220 |
-0,00291 |
|
145 |
225 |
-0,00162 |
|
145 |
230 |
-0,00076 |
|
145 |
235 |
-0,00027 |
145 |
310 |
-0,02213 |
|
145 |
315 |
-0,02402 |
|
145 |
320 |
-0,02460 |
|
145 |
325 |
-0,02369 |
9

|
Варіант № 9 |
|
|
Варіант № 10 |
|
|
Варіант № 11 |
|
|
Варіант № 12 |
|||||||
35 |
|
60 |
0,00040 |
|
35 |
|
65 |
0,00003 |
|
35 |
70 |
0,00000 |
|
35 |
|
75 |
0,00001 |
35 |
|
150 |
0,14041 |
|
35 |
|
155 |
0,11598 |
|
35 |
160 |
0,08513 |
|
35 |
|
165 |
0,05086 |
35 |
|
240 |
-0,00040 |
|
35 |
|
245 |
-0,00003 |
|
35 |
250 |
0,00000 |
|
35 |
|
255 |
-0,00001 |
35 |
|
330 |
-0,14041 |
|
35 |
|
335 |
-0,11598 |
|
35 |
340 |
-0,08513 |
|
35 |
|
345 |
-0,05086 |
70 |
|
60 |
0,00100 |
|
70 |
|
65 |
0,00008 |
|
70 |
70 |
0,00000 |
|
70 |
|
75 |
0,00004 |
70 |
|
150 |
0,34809 |
|
70 |
|
155 |
0,28752 |
|
70 |
160 |
0,21105 |
|
70 |
|
165 |
0,12610 |
70 |
|
240 |
-0,00100 |
|
70 |
|
245 |
-0,00008 |
|
70 |
250 |
0,00000 |
|
70 |
|
255 |
-0,00004 |
70 |
|
330 |
-0,34809 |
|
70 |
|
335 |
-0,28752 |
|
70 |
340 |
-0,21105 |
|
70 |
|
345 |
-0,12610 |
110 |
|
60 |
0,00063 |
|
110 |
|
65 |
0,00005 |
|
110 |
70 |
0,00000 |
|
110 |
|
75 |
0,00002 |
110 |
|
150 |
0,21834 |
|
110 |
|
155 |
0,18035 |
|
110 |
160 |
0,13238 |
|
110 |
|
165 |
0,07909 |
110 |
|
240 |
-0,00063 |
|
110 |
|
245 |
-0,00005 |
|
110 |
250 |
0,00000 |
|
110 |
|
255 |
-0,00002 |
110 |
|
330 |
-0,21834 |
|
110 |
|
335 |
-0,18035 |
|
110 |
340 |
-0,13238 |
|
110 |
|
345 |
-0,07909 |
145 |
|
60 |
0,00006 |
|
145 |
|
65 |
0,00000 |
|
145 |
70 |
0,00000 |
|
145 |
|
75 |
0,00000 |
145 |
|
150 |
0,02129 |
|
145 |
|
155 |
0,01759 |
|
145 |
160 |
0,01291 |
|
145 |
|
165 |
0,00771 |
145 |
|
240 |
-0,00006 |
|
145 |
|
245 |
0,00000 |
|
145 |
250 |
0,00000 |
|
145 |
|
255 |
0,00000 |
145 |
|
330 |
-0,02129 |
|
145 |
|
335 |
-0,01759 |
|
145 |
340 |
-0,01291 |
|
145 |
|
345 |
-0,00771 |
|
Варіант № 13 |
|
|
Варіант № 14 |
|
|
Варіант № 15 |
|
|
Варіант № 16 |
|||||||
35 |
|
80 |
0,00029 |
|
35 |
|
85 |
0,00153 |
|
35 |
90 |
0,00481 |
|
30 |
|
15 |
0,05292 |
35 |
|
170 |
0,01651 |
|
35 |
|
175 |
-0,01471 |
|
35 |
180 |
-0,04012 |
|
30 |
|
105 |
0,02850 |
35 |
|
260 |
-0,00029 |
|
35 |
|
265 |
-0,00153 |
|
35 |
270 |
-0,00481 |
|
30 |
|
195 |
-0,05292 |
35 |
|
350 |
-0,01651 |
|
35 |
|
355 |
0,01471 |
|
35 |
360 |
0,04012 |
|
30 |
|
285 |
-0,02850 |
70 |
|
80 |
0,00071 |
|
70 |
|
85 |
0,00379 |
|
70 |
90 |
0,01191 |
|
65 |
|
15 |
0,16316 |
70 |
|
170 |
0,04093 |
|
70 |
|
175 |
-0,03647 |
|
70 |
180 |
-0,09947 |
|
65 |
|
105 |
0,08786 |
70 |
|
260 |
-0,00071 |
|
70 |
|
265 |
-0,00379 |
|
70 |
270 |
-0,01191 |
|
65 |
|
195 |
-0,16316 |
70 |
|
350 |
-0,04093 |
|
70 |
|
355 |
0,03647 |
|
70 |
360 |
0,09947 |
|
65 |
|
285 |
-0,08786 |
110 |
|
80 |
0,00045 |
|
110 |
|
85 |
0,00238 |
|
110 |
90 |
0,00747 |
|
115 |
|
15 |
0,08970 |
110 |
|
170 |
0,02567 |
|
110 |
|
175 |
-0,02287 |
|
110 |
180 |
-0,06239 |
|
115 |
|
105 |
0,04830 |
110 |
|
260 |
-0,00045 |
|
110 |
|
265 |
-0,00238 |
|
110 |
270 |
-0,00747 |
|
115 |
|
195 |
-0,08970 |
110 |
|
350 |
-0,02567 |
|
110 |
|
355 |
0,02287 |
|
110 |
360 |
0,06239 |
|
115 |
|
285 |
-0,04830 |
145 |
|
80 |
0,00004 |
|
145 |
|
85 |
0,00023 |
|
145 |
90 |
0,00073 |
|
150 |
|
15 |
0,00518 |
145 |
|
170 |
0,00250 |
|
145 |
|
175 |
-0,00223 |
|
145 |
180 |
-0,00608 |
|
150 |
|
105 |
0,00279 |
145 |
|
260 |
-0,00004 |
|
145 |
|
265 |
-0,00023 |
|
145 |
270 |
-0,00073 |
|
150 |
|
195 |
-0,00518 |
145 |
|
350 |
-0,00250 |
|
145 |
|
355 |
0,00223 |
|
145 |
360 |
0,00608 |
|
150 |
|
285 |
-0,00279 |
10
