
Конспект лекцій Паляниця
.pdf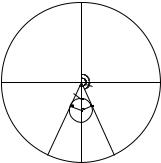
S
E |
Z |
AW |
W |
|
AE |
||
BK |
|
|
|
|
|
|
|
E |
t |
|
|
W |
|
||
|
P |
|
|
|
N |
|
|
СN В
Рис. 27. Елонгація світил.
У моменти елонгації вертикал світила (на рис. 26 це лінія ZB для західної елонгації та лінія ZC для східної елонгації) має спільну з добовою паралеллю дотичну пряму, тобто, видимий добовий рух світила відбувається уздовж його вертикала. Оскільки коло схилень (на рис. 26 це лінії PNσW і PNσЕ) завжди перетинає добову паралель під прямим кутом, то паралактичний кут
PN Z стає прямим, а трикутник |
PN Z |
– прямокутним. Розв’язуючи отриманий прямокутний |
|||||||||||||
паралактичний трикутник за правилом Непера-Модюі, можна знайти вирази для t, z, A : |
|||||||||||||||
|
|
|
cost tg / tg , |
|
|
|
|
|
|||||||
|
|
|
cos z sin / sin , |
|
|
|
|||||||||
|
|
|
sin A cos / cos . |
|
|
||||||||||
Оскільки світила, які мають елонгацію, можуть знаходитися у двох положеннях: західній або |
|||||||||||||||
східній елонгації, то для західної елонгації шукані величини будуть |
|
||||||||||||||
A |
|
|
A, t |
24 |
h |
t, |
s |
t , |
|||||||
180 |
|
||||||||||||||
w |
|
|
|
|
W |
|
|
|
|
|
|
|
W |
|
W |
для східної елонгації |
A |
180 |
|
A, |
t |
|
t, |
s |
|
t . |
|||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
E |
|
|
|
|
E |
|
E |
|
|
Спостереження світил в елонгації виконують при дослідженнях астрономічних теодолітів у польових умовах.
Ефемерида Полярної зорі.
Ефемеридою світила називається таблиця його координат, в якій аргументом є час. У геодезичній астрономії ефемериди представляють собою таблицю координат світил, які будуть спостерігатися, в горизонтній системі координат (z, A) з кроком в часі, що забезпечує точність
цих координат ±1'. Такі ефемериди називають робочими. Вони складаються на період спостережень для забезпечення легкого і швидкого знаходження світил на небесній сфері за допомогою астрономічного приладу. Нагадаємо, що всі астрономічні прилади мають вертикальний круг, відліки якого відповідають зенітній відстані спостережуваного світила. Щодо азимута світила, то це буде відлік горизонтального круга у разі виконання орієнтування приладу.
При польових астрономічних спостереженнях в північній півкулі для орієнтування інструмента часто використовують Полярну. Складання ефемерид Полярної виконується
наступним чином. |
У пункті |
з широтою |
для спостереження |
зорі з |
координатами , |
на |
|
проміжок часу від |
s1 до sk |
потрібно скласти таблицю значень |
A і z . Полярна відстань |
|
|||
Полярної зорі не перевищує 1º. Тому паралактичний трикутник |
PN Z |
є вузьким сферичним |
|||||
трикутником (рис. 28). |
|
|
|
|
|
|
|
З вершини |
цього трикутника опустимо |
сферичний перпендикуляр K на меридіан. |
|||||
Отримаємо два прямокутних трикутники PN K |
(елементарний) |
і K Z |
(вузький). Розв’язуючи |
||||
трикутник PN K як плоский, можна записати
PN K f cost, K x sin t,
де t s .
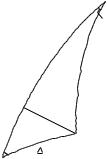
Розглянемо
KZ 90º ( f )
|
|
|
|
|
Z |
|
|
|
|
|
A |
|
|
|
|
|
N |
|
|
f) |
|
|
|
|
|
|
|
z |
|
|
|
K |
x |
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
N |
|
|
|
|
Рис. 28. Паралактичний трикутник для Полярної. |
||||
розв’язок |
прямокутного трикутника |
K Z . У ньому |
|||
і |
K x |
. За правилом Непера-Модюі |
|
||
|
|
tgz tg(90º f ) / cos AN . |
|||
Для обчислення |
z |
з помилкою 1' можна прийняти 1/ cos A 1, тоді |
|
|
z 90º ( f ), h f . |
відомі дві сторони
З трикутника K Z
sin x sin AN sin z ,
або, приймаючи до уваги малість величин можна записати
x
і AN , при обчисленні азимута з точністю до 1'
x A |
sin z A |
cos( |
N |
N |
|
f
)
.
Звідси
AN
x / cos(
f ) sin( s ) / cos(
f
)
.
У наведених формулах азимут Полярної, відраховані від точки півдня
AN S ,
відраховується від точки визначаються за формулою
A |
180º A . |
S |
N |
півночі N . Азимути
AS
Системи вимірювання часу.
У попередніх розділах були розглянуті основні системи небесних координат, за допомогою яких задається положення небесних світил на небесній сфері. Враховуючи, що всі світила є рухомими об'єктами, виникає, як необхідний, фактор фіксування часу спостереження світила в конкретному його положенні на небесній сфері. Спочатку для вимірювання часу, тобто завдання шкали часу, вибирався періодично повторюваний процес або явище. У першу чергу звернули увагу на три таких явища: це зміна дня і ночі, зміна фаз Місяця і зміна пір року. Періоди повторення цих явищ були покладені в основу трьох основних одиниць вимірювання часу: добу, синодичний місяць і рік. Взагалі побудовою астрономічних шкал часу займаються національні служби часу і Міжнародне бюро часу. На даний час в основі всіх відомих способів побудови безперервних шкал часу лежать наступні періодичні процеси:
-обертання Землі навколо своєї осі;
-обертання Землі навколо Сонця;
-обертання Місяця навколо Землі по орбіті;
-коливання маятника під дією сили тяжіння;
-пружні коливання кристала кварцу під дією змінного струму;
-електромагнітні коливання молекул і атомів;
-радіоактивний розпад ядр атомів та інші процеси.
Перший із названих періодичних процесів – обертання Землі навколо своєї осі, є надзвичайно рівномірним, не обмеженим у часі, безперервним протягом усього існування людства, тому слугує еталоном вимірювання часу у заданні доби. Цей процес покладений в основі двох систем вимірювання часу – зоряній і сонячній. Також у геодезичній астрономії, астрометрії і небесній механіці використовуються системи:
-ефемеридного і динамічного часу, як ідеальна побудова рівномірної шкали часу,
-атомного часу, як практична реалізація ідеально рівномірної шкали часу.
Система зоряного часу.
Періоди обертання Землі навколо своєї осі щодо зірок і Сонця різні. Один повний оберт щодо зірок Земля робить за менший проміжок часу, ніж відносно Сонця. Пояснюється це рухом Сонця по екліптиці в тому ж напрямку, в якому відбувається обертання Землі. Таким чином, рівномірність зоряного часу визначається тільки рівномірністю обертання Землі. Вимірювання зоряного часу, в кінцевому підсумку, зводиться до визначення кута між площинами небесного меридіана і кола схилення світила, тобто годинного кута t світила. При розгляді екваторіальної системи координат було введено поняття зоряного часу як годинного кута точки весняного рівнодення, тобто мірою зоряного часу є годинний кут t точки весняного рівнодення. Таким
чином, початковою точкою на небесній сфері для даної системи є точка весняного рівнодення , а за нуль-пункт (початок зоряної доби) прийнято момент верхньої кульмінації точки . Відповідно,
зоряна доба визначається як інтервал часу між двома послідовними верхніми кульмінаціями точки весняного рівнодення.
Зоряний час позначається буквою s . Як згадувалося раніше, пряме сходження світила α і його годинний кут t пов'язані із зоряним часом s простим співвідношенням, яке справедливе для будь-якого світила
s t t .
Отже, знаючи пряме сходження світила і обчислюючи його годинний кут t , можна визначити зоряний час s .
Однак для повсякденного життя зоряний час є непридатним, тому що зоряна доба коротша за сонячну. Пояснюється це зміщенням Сонця по екліптиці, в наслідок чого час верхньої кульмінації точки весняного рівнодення протягом року зміщується щодо часу верхньої кульмінації Сонця і відбувається в різний час доби.
Для отримання менших проміжків часу зоряну добу ділять на 24 зоряних години, годину – на 60 зоряних хвилин, хвилину – на 60 зоряних секунд. Оскільки небесна сфера робить повний оберт за одну зоряну добу, то за 1 зоряний час вона повертається на 15o, за хвилину – на 15', за секунду – на 15".
Система зоряного часу застосовується при визначенні географічних координат пунктів на поверхні Землі і азимутів напрямків на земні предмети, при вивченні нерівномірностей добового обертання Землі, при встановленні нуль-пунктів шкал інших систем вимірювання часу. Не зважаючи на широке застосування цієї системи в астрономії, у повсякденному житті вона є незручною. Зміна дня і ночі, обумовлена видимим добовим рухом Сонця, створює цілком визначений цикл в діяльності людини на Землі. Тому здавна числення часу ведеться за добовим рухом Сонця.
Системи істинного і середнього сонячного часу. Рівняння часу.
Другою системою часу, пов'язаною з обертанням Землі навколо своєї осі є система сонячного часу, в якій розрізняють системи істинного і середнього сонячного часу. Взагалі, на відміну від зоряного, сонячний час відповідає вимогам повсякденного життя людини, але визначити його набагато складніше. Пояснюється це тим, що при астрономічних або геодезичних спостереженнях Сонця застосовується істинний сонячний час m , який знаходиться у функціональній залежності щодо годинного кута Сонця, та використовується для визначення істинної сонячної доби як проміжку цього часу між двома послідовними нижніми кульмінаціями центру істинного Сонця.
, який знаходиться у функціональній залежності щодо годинного кута Сонця, та використовується для визначення істинної сонячної доби як проміжку цього часу між двома послідовними нижніми кульмінаціями центру істинного Сонця.
Початковою точкою даної системи часу є центр диска істинного Сонця, а нуль-пунктом – істинна опівніч або момент нижньої кульмінації центра диска істинного Сонця. Мірою істинного сонячного часу є геоцентричний годинний кут істинного Сонця t плюс 12 годин
плюс 12 годин
m = t
= t + 12h.
+ 12h.
Одиниця істинного сонячного часу – секунда, що дорівнює 1/86400 істинної сонячної доби, не задовольняє основній вимозі, висунутій до одиниці виміру часу – вона не є сталою. Причинами несталості шкали істинного сонячного часу є в першу чергу еліптичність орбіти Землі. В наслідок цього, поблизу перигелію (на початку січня), швидкість Землі максимальна і за істинну сонячну добу вона зміщується на 61,1' стосовно напрямку на Сонце, а поблизу афелію (на початку липня) –

всього на 57,2'. Тому істинна сонячна доба взимку довша, а влітку – коротша. Нерівномірність істинних сонячних діб внаслідок еліптичності земної орбіти можна представити синусоїдою з амплітудою 7,6 хвилини і початковою фазою в перигелії 4 січня.
Крім того, внаслідок нахилу екліптики до екватора рівні ділянки екліптики, по яких рухається Сонце по небесній сфері, в проекції на екватор дають нерівні відрізки, що також впливає на нерівномірність істинного сонячного часу. Цю нерівномірність можна представити синусоїдою з амплітудою 9,8 хвилини, періодом півроку і початковою фазою в день весняного рівнодення.
Внаслідок цих причин застосування системи істинного сонячного часу на практиці є незручним. З метою отримання рівномірного сонячного часу було введено поняття середнього екваторіального Сонця – фіктивної точки, що рівномірно рухається по небесному екватору в тому ж напрямку, що й істинне Сонце, з періодом 1 рік ( ~ 365,2422 діб). Годинний кут середнього екваторіального Сонця визначає середній сонячний час, а проміжок часу між двома послідовними нижніми кульмінаціями середнього екваторіального Сонця називається середньою сонячною добою. Момент верхньої кульмінації середнього екваторіального Сонця (середній опівдень) до 1925 року приймався за початок середніх сонячних діб, а з 1 січня 1925 року за міжнародною угодою вважається рівним 12 годинам, оскільки початок календарної доби припадає на опівніч. Середня сонячна доба зберігає постійну тривалість.
Перехід до рівномірної шкали сонячного часу відбувається в два етапи.
Етап 1 – перехід до фіктивного середнього екліптичного Сонця. На даному етапі виключається нерівномірність руху Сонця по екліптиці. Нерівномірний рух по еліптичній орбіті замінюється рівномірним рухом по орбіті. Істинне Сонце і середнє екліптичне Сонце збігаються, коли Земля проходить через перигелій і афелій своєї орбіти.
Етап 2 – перехід до середнього екваторіального Сонця. Тут виключається нерівномірність зростання прямого сходження Сонця, зумовленого нахилом екліптики до екватора. Істинне Сонце та середнє екваторіальне Сонце одночасно проходять точки весняного та осіннього рівнодення. В результаті перерахованих дій вводиться нова система вимірювання часу – середній сонячний час, що позначається буквою m .
Початковою точкою даної системи часу є центр диску середнього екваторіального Сонця, а нуль-пунктом – середня опівніч або момент нижньої кульмінації середнього екваторіального Сонця. Мірою середнього часу є геоцентричний годинний кут середнього екваторіального Сонця –
t екв плюс 12 |
годин: |
m = t екв + 12h.
екв + 12h.
Визначити середній сонячний час безпосередньо зі спостережень не можна, оскільки середнє
екваторіальне Сонце, як вказано раніше, є фіктивною |
точкою на небесній сфері. Середній |
|||
сонячний час обчислюють за істинним сонячним часом, |
визначеним зі спостережень істинного |
|||
Сонця. Різниця істинного |
сонячного часу |
m і середнього сонячного часу |
m називається |
|
рівнянням часу і позначається |
: |
|
|
|
|
m |
- m = t - t екв. |
|
|
На підставі відомих закономірностей руху Землі ця величина може бути заздалегідь обчислена для будь-якого моменту часу. Наближене значення рівняння часу в залежності від порядкового номера дня у році можна отримати як різницю двох описаних вище нерівномірностей довжини істинних сонячних діб:
1 2 7,7m sin(1 79 ) 9,5m sin 2l ,
де l – екліптична довгота середнього екліптичного Сонця. Перший доданок враховує нерівномірність руху Землі по орбіті, другий – проекція на екватор руху Сонця по екліптиці. Протягом року значення чотири рази дорівнює нулю (близько 15 квітня, 14 червня, 1 вересня і
25 грудня) і чотири рази досягає крайніх значень (11 лютого, 15 травня, 26 липня і 3 листопада), відповідно +14,3 хв., -3,7 хв., +6,4 хв. і -16,4 хв. Найшвидше (до 30 с на добу) рівняння часу змінюється в грудні.
|
18 |
|
|
|
|
|
12 |
|
|
|
|
|
6 |
|
|
|
|
|
0 |
|
|
|
|
|
-6 |
|
|
|
|
|
-12 |
|
|
|
|
|
-18 |
|
|
|
|
|
0 |
90 |
180 |
270 |
360 |
|
|
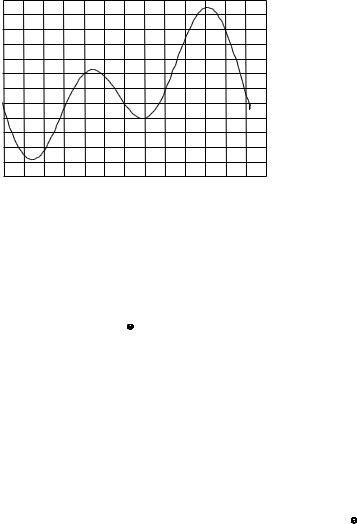
Рис. 29. Графік рівняння часу. |
|
||
Графіком |
є крива з двома максимумами і двома мінімумами, яка в декартовій прямокутній |
||||
системі координат має вигляд, показаний на рис. 29, на якому по вертикальній осі відкладено значення в хвилинах часу, по горизонталі – дні року. В Астрономічному Щорічнику на кожну
дату наводиться величина E , що дорівнює |
E 12 |
h |
. З даною величиною зв'язок між середнім |
||||||||||
|
|||||||||||||
сонячним часом і годинним кутом істинного Сонця визначається виразом |
|||||||||||||
|
|
|
|
m = t - E. |
|
|
|
|
|||||
Місцевий час на різних меридіанах. Всесвітній, поясний і декретний час. |
|||||||||||||
Час на меридіані даного пункту з |
довготою |
|
|
|
називається місцевим. Друга теорема |
||||||||
сферичної астрономії про різниці годинних кутів світила для допоміжних точок запишеться: |
|||||||||||||
t |
A |
t |
B |
s |
A |
s |
B |
|
|
A |
|
B |
, |
|
|
|
|
|
|
|
|
||||||
t А – t
А – t В = m
В = m А – m
А – m В = λA – λB,
В = λA – λB,
t еквА – t
еквА – t еквВ = m
еквВ = m еквА – m
еквА – m еквВ = λA – λB.
еквВ = λA – λB.
Звідси випливає, що різниця місцевих часів двох пунктів дорівнює різниці довгот цих пунктів. У географічній системі координат гринвіцький меридіан прийнятий за початковий –
0 |
h |
. Місцевий час на меридіані Гринвіча позначається великими літерами S,M ,M. Середній |
|
сонячний час M на меридіані Гринвіча називається Всесвітнім часом і позначається UT (Universal Time). З наведених формул випливає:
s S  WE ,
WE ,
m M  WE ,
WE ,
m UT  WE .
WE .
Ці співвідношення лежать в основі методу визначення довгот польових пунктів: місцевий час визначається за годинним кутом світила, гринвіцький – за радіосигналами точного часу.
У повсякденному житті використання місцевого часу є незручним, оскільки на різних меридіанах місцевий час різний, навіть у межах одного міста. Тому введена система вимірювання часу за годинними поясами – поясний час Tn , де n – номер пояса. На поверхні Землі вибрані 24
меридіани через 15º, з довготами n , рівними відповідно |
0 |
h |
h |
h |
. Ці меридіани є осьовими для |
|
,1 |
,....23 |
24-х годинних поясів з номерами від 0 до 23. У межах кожного годинного поясу показ годин установлюють за часом осьового меридіана, що рівний середньому сонячному часу m на цьому меридіані:
Tn m .
Різниця поясних часів у двох пунктах дорівнює різниці довгот осьових меридіанів або різниці номерів їх годинних поясів:
Tn1 Tn2 n1 n2 n1 n2 .
Гринвіцький меридіан є осьовим у нульовому годинному поясі (n 0) , а Всесвітній час UT є поясним часом нульового годинного поясу
UT T0 , Tn T0 n UT n .
З 16 липня 1930 р. декретом Уряду СРСР стрілки годинника були переведені щодо поясного
часу на 1 годину вперед. Такий час отримав назву декретного, що позначається |
Dn |
. З 1981 р. у |
СРСР уведено літній час (додаванням 1 години), який діє з останньої неділі березня до останньої неділі жовтня. Таким чином, декретний час є:
|
|
|
|
|
Dn Tn k , |
де |
k 2 |
h |
для літнього часу, |
h |
|
|
k 1 – для зимового. Декретний час можна обчислити за |
||||
такою формулою |
|
|
|||
|
|
|
Dn |
UT (n k) m [(n k) E ] . |
|
Декретний, поясний і всесвітній час – варіанти системи середнього сонячного часу, утворені лише зміщенням нуль-пунктів на сталу величину.
Примітка: В Україні, після проголошення незалежності, було скасовано декретний час.
Зв'язок між середнім сонячним часом і зоряним часом.
Системи середнього сонячного m і зоряного s часу засновані на добовому обертанні Землі, але мають різний масштаб – різну тривалість діб. Різниця масштабів обумовлена тим, що Земля, крім добового руху навколо осі, здійснює річний рух навколо Сонця.
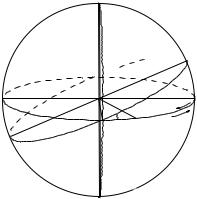
Нехай початок зоряної і сонячної діб збігаються. Земля бере участь у двох рухах (добовому і річному), тому через одну добу Земля пройде по орбіті відстань, рівною дузі γF – приблизно 1º
(або 4 |
m |
), і зоряна доба закінчиться раніше сонячної на величину, приблизно рівною |
4 |
m |
(див. рис. |
|||
|
|
|
||||||
30). Точне значення величини, на яку відрізняється зоряна та середня сонячна доба є |
24 |
h |
/365,2422 |
|||||
|
||||||||
|
|
m |
s |
. |
|
|
|
|
доби = 3 56,555 |
|
|
|
|
|
|||
Через 365,2422 доби Сонце знову пройде точку весняного рівнодення . Такий проміжок часу між двома послідовними проходженнями істинного Сонця через точку весняного рівнодення, що містить 365,2422 доби, називається тропічним роком. Враховуючи попереднє зауваження стосовно різниці між сонячною і зоряною добою, за один рік різниця у кількості діб сягає однієї доби, тобто, тропічний рік містить 366,2422 зоряних діб.
Звідси
де
одиниць
тобто
|
1 сер. сон. доба = (366,2422/365,2422) зор. діб = (1 + ) зор. діб, |
|
= 1/365,2422 = 0,00273791 – масштабний коефіцієнт переходу від середніх сонячних |
до зоряних. Отже, |
m |
середніх одиниць часу містять (1 )m одиниць зоряного часу, |
s (1 )m .
P
N
 Z
Z



 E
E


Q`
O
F
E`
PS
|
|
ух |
|
.р |
|
об |
|
|
Д |
|
|
|
|
х |
|
|
ру |
|
н. |
|
іч |
|
|
Р |
|
|
Q
Рис. 30. Нерівність зоряних і сонячних діб.
Для зворотного переходу від зоряного до середнього сонячного часу є справедливим вираз
1 зор. доба = 365,2422/366,2422 сер. сон. діб = (1 - ) сер. сон. діб,
де = 1/366,2422 = 0,00273043 – масштабний коефіцієнт переходу від зоряних одиниць до середніх сонячних. Отже, s зоряних одиниць часу містять (1 )s одиниць середнього сонячного
часу
m (1 )s .
Ці формули дають можливість переходу від інтервалів середнього сонячного часу до інтервалів зоряного часу і навпаки.
Зоряний час в середню опівніч на різних меридіанах.
У момент середньої опівночі (нижньої кульмінації середнього екваторіального Сонця)
годинний кут середнього екваторіального Сонця дорівнює буде
12 |
h |
|
, а зоряний час в середню опівніч
so = α сер.екв. + 12h.
сер.екв. + 12h.
Зоряний час в опівніч на меридіані Гринвіча позначається So. В Астрономічному Щорічнику публікуються значення So на кожен день року. Вираз для So на будь-яку дату знаходиться за формулою
дати,
де
T
So = 6h41m50,55s + 236,555s d + 0,093104s T2 – 6,27∙10-6T3,
d– число діб, що пройшли від епохи 2000, січень, 1 до Гринвіцької опівночі розглянутої
–проміжок часу, виражений в юліанських століттях по 36525 діб, тобто
T (JD 2451545) / 36525 .
Оскільки на різних меридіанах опівніч настає неодночасно, то зоряний час в місцеву опівніч на різних меридіанах не є однаковим. Момент soE на схід від Гринвіча настає раніше від So, а момент soW (на захід) – пізніше. В одному і тому ж пункті зоряний час опівночі за добу
збільшується на величину буде відрізнятися від So на
24h , а за проміжок часу,
,тобто
s |
о |
S |
о |
|
|
|
|
рівний
W .
E
, зоряний час в місцеву опівніч
Перехід від зоряного часу до середнього і навпаки.
Перехід від зоряного часу s до середнього |
m і навпаки можна пояснити, скориставшись рис. |
|||
31. Фактично фізичний час вимірюється двома шкалами: середньою сонячною і зоряною. |
||||
|
|
Середній сонячний час |
|
|
m=0 |
h |
m |
m=0 |
h |
|
||||
|
|
|||
|
|
|
|
Час |
so |
|
s |
so |
|
|
|
Зоряний час |
|
|
|
Рис. 31. Зв'язок між зоряним і середнім сонячним часом. |
|||
На початку доби середній сонячний час m |
дорівнює 0h, а зоряний – so. З рисунку видно, що |
|||
середній сонячний час |
|
m в середині доби дорівнює проміжку часу (s - so), що переведений у |
||
середні сонячні одиниці |
|
|
|
|
|
|
m = (s - so)(1 – v) = (s - so) - (s - so)v , |
а зоряний час |
s |
є час опівночі so плюс інтервал середнього сонячного часу |
зоряні одиниці |
|
|
s = so + m(1 + μ) = so + m + mμ.
Для Гринвіцького меридіана формули є аналогічними
UT = (S – So)(1 – v) = (S – So) – (S – So)v, S = So + UT(1 + μ) = So + UT + UT μ.
m
, переведений у
Ефемеридний час.
Ідеально рівномірна шкала часу введена ухвалою 8-го з'їзду Міжнародного Астрономічного Союзу у 1952 р.
1.Механізм – обертання Землі протягом року навколо Сонця.
2.Масштаб – тривалість одної ефемеридної секунди, що рівна 1/31556925,9747 тропічного
року.
Оскільки тропічний рік не є сталим, то за еталон прийнята тривалість конкретного тропічного року у фундаментальну епоху 1900.0, січень, 0, 12h ET .
3. Нуль-пункт – фундаментальна епоха 1900.0, січень, 0, 12h ET на початковому меридіані.
4. Спосіб відліку – за посередництвом системи Всесвітнього часу |
UT , добавлянням |
поправки за перехід до ефемеридного часу |
|
ET UT T , |
|
де T – поправка за вікове сповільнення обертання Землі, яку отримують зі спостережень Місяця і публікують в Астрономічному Щорічнику.
У першому наближенні систему ET можна представити як систему, засновану на добовому обертанні Землі, але виправлену за нерівномірність цього обертання. Оскільки ефемеридна секунда прив'язана до тривалості цілком певного року, еталон ET не може бути відтворений – це ідеальна побудова. Шкала ET існувала до 1986 року, а потім була замінена динамічним часом.
Динамічний час.
З 1986 року шкала ефемеридного часу ET замінена двома шкалами динамічного часу DT : 1) земний динамічний час TDT , рівний за масштабом ET , віднесений до центру мас Землі і
служить незалежним аргументом видимих геоцентричних ефемерид, у тому числі при визначенні ефемерид ШСЗ;
2) барицентричний динамічний час TDB , який враховує рух центру мас Сонця навколо центру мас всієї Сонячної системи (барицентра Сонячної системи), віднесений до барицентру Сонячної системи і є аргументом диференціальних рівнянь всіх гравітаційних теорій руху тіл Сонячної системи у Ньютоновому наближенні. Різниці TDB і TDT полягають у періодичних варіаціях масштабу з амплітудою 0,00166 сек.
Атомний час
З появою у 1955 р. надстабільних еталонів частоти, основаних на квантових переходах між енергетичними рівнями молекул і атомів, стало можливим створення атомних шкал часу. Атомний
час |
TAI |
- час, в основу вимірювання якого покладені електромагнітні коливання, що |
випромінюється атомами або молекулами при переході з одного енергетичного стану в інший.
За уточненням і доповненням Консультативного комітету із визначення секунди: TAI - координатний час, який визначається в геоцентричній системі відліку з одиницею виміру, що
дорівнює секунді CI на геоїді, який обертається. |
|
|
Масштаб системи TAI |
прийнятий рівним масштабові |
ET , тобто атомний годинник є |
фізичне відтворення шкали ефемеридного часу ET . Точність відтворення до 2·10-12 сек. Ухвалою |
||
XII Генеральної конференції мір і ваг у 1967 році одиниця |
TAI 1 атомна секунда прирівняна |
|
тривалості 9192631770 періодів випромінювання, що відповідає переходу між двома надтонкими рівнями основного стану атома цезію 133. Відносна точність цезієвого еталона частоти 10-10÷10-11 протягом декількох років.
Нуль-пункт шкали TAI зміщений щодо нуль-пункту шкали ET на сталу величину
ET
TAI
32,184 |
s |
|
.
Еталон атомного часу не має ні добових, ні вікових коливань, не старіє і володіє достатньою визначеністю, точністю та відтворюваністю.
Системи Всесвітнього часу. Всесвітній координований час.
Всесвітній час UT, за визначенням, є середній сонячний час на меридіані Гринвіча. З огляду на нерівномірність обертання Землі Гринвіцький меридіан також обертається нерівномірно. Крім того, внаслідок безперервного зміщення осі обертання в тілі Землі географічні полюси зміщуються по поверхні Землі, а разом з ними змінюють своє положення і площини істинних меридіанів. Через ці фактори виділяють наступні системи виміру часу:
●UT0 – час на миттєвому Гринвіцькому меридіані, визначений за миттєвим положенням полюсів Землі. Це час, безпосередньо отриманий з астрономічних спостережень;
●UT1 - час на середньому Гринвіцькому меридіані, виправлений за рух полюсів,
UT1 UT0 ,
де - поправка, що залежить від координат миттєвого полюса, що відраховуються відносно загальноприйнятого середнього полюса;
● UT2 - час, виправлений за сезонну нерівномірність обертання Землі Ts ,
|
UT 2 UT1 Ts . |
|
|
|
|
Для узгодження спостережуваного всесвітнього часу UT1 |
та строго рівномірного часу |
TAI |
з |
1964 року введено рівномірно-змінну шкалу часу UTC – всесвітній координований час. Масштаби |
||||
UTC |
і TAI рівні, а нуль-пункт змінюється стрибком. Між UTC |
і UT1 накопичується розбіжність, |
||
обумовлена, по-перше, нерівномірністю шкали UT1, а, по-друге, нерівністю масштабів UT1 |
і TAI |
|||
(1 атомна секунда не дорівнює точно 1 секунді UT1). При накопиченні розходження між UTC |
і |
|||
UT1 |
до 0,9 секунди проводиться корегування стрибком на 1сек. |
|
|
|
|
UTC TAI b , |
|
|
|
де
b
1 |
s |
|
, якщо
 UTC
UTC
UT1
> 0,9
s
або b 0s , якщо
 UTC UT1
UTC UT1
< 0,9
s
. Про моменти введення
поправки на 1s телебаченню в
заздалегідь повідомляється у пресі. Сигнали точного часу передаються по радіо і системі UTC .
Фактори, що викликають зміни координат світил.
Відомо, що горизонтні координати |
z |
і |
A |
світил, а також годинний кут |
t |
з першої |
екваторіальної системи координат безперервно змінюються внаслідок добового обертання небесної сфери. Координати другої екваторіальної системи ( і ) та екліптичні координати ( b і l ) від добового обертання не залежать.
Однак, існують фактори, які викликають зміни як горизонтних, так і екваторіальних та екліптичних координат. Оскільки ці зміни необхідно враховувати при опрацюванні астрономічних визначень, розглянемо причини, що їх викликають, і методи їх врахування.
Одною із таких причин є астрономічна рефракція. Наявність земної атмосфери викликає зміну напрямку світлового променя, що йде від світила до ока спостерігача. Враховуючи вплив астрономічної рефракції на координати світил, ми якби отримуємо координати з поверхні, що є без земної атмосфери.
Наступною із таких причин є те, що астрономічні спостереження проводяться з різних точок земної поверхні, що викликає зміни напрямку на світило і робить неспівставимими між собою спостереження одного і того ж світила, що виконані в один і той же момент часу. Аналогічні зміни напрямків на спостережувані світила викликає обертання Землі. Це явище називається добовим паралаксом. Звільнивши координати світил, отримані зі спостережень, від впливу добового паралаксу, ми тим самим приводимо результати спостережень до центру Землі.
Спостерігач, що знаходиться на поверхні Землі, приймає участь у річному русі Землі навколо Сонця, що також викликає відповідні зміни напрямків на світила, а, відповідно, і координат світил, отриманих із спостережень в різних точках земної орбіти. Це явище називається річним паралаксом. Враховуючи вплив річного паралаксу на координати світил, ми приводимо ці координати до центру Сонця.
Наступною причиною, що викликає зміну координат світил, є добова і річна аберація. Річ у тому, що швидкість обертання Землі і швидкість її річного руху навколо Сонця не є величинами нескінченно малими порівняно зі швидкістю поширення світла. Внаслідок цього спостерігач, що знаходиться на поверхні Землі, бачить світило зміщеним з його істинного місця по дузі великого кола до тої точки небесної сфери, в яку в даний момент направлений вектор швидкості спостерігача. Звільнивши отримані зі спостережень координати світил від впливу добової та річної аберації, ми відносимо їх до нерухомої Землі, ніби зупиняючи обертання довкола осі та її річний рух навколо Сонця.
Враховуючи вплив астрономічної рефракції, добового та річного паралаксу, добової та річної аберації, ми тим самим враховуємо вплив факторів, що спотворюють положення світил на небесній сфері. Якби небесний екватор і точка весняного рівнодення не змінювали свого положення у просторі, то після врахування впливу названих факторів координати світил, що не мають власних рухів, залишались би незмінними.
Однак, самі координатні площини і основні напрямки внаслідок гравітаційних явищ у сонячній системі змінюють своє положення у просторі. Під дією місячно-сонячного притягання полюс світу повільно переміщується поміж зірок, що викликає зміщення небесного екватора і точки весняного рівнодення. Інакше кажучи, сама система відліку з плином часу змінює своє положення по відношенню до нерухомих зірок. Внаслідок цього координати світила, отримані зі спостережень, що відносяться до різних моментів часу (до різних епох), будуть різними навіть у тому випадку, якщо враховані всі фактори, що спотворюють його положення на небесній сфері. Для порівняння координат світила, що відносяться до різних моментів часу, положення системи координат для певного моменту часу приймається за початкове і до нього приводяться координати, що відносяться до будь-яких інших моментів.
Віковий рух полюса світу, що викликає зміщення системи відліку, називається прецесією, а періодичний – нутацією.
Існує ще одна причина зміни координат світил – так званий власний рух зірок у просторі (у напрямку перпендикулярному променю зору).
Враховуючи вплив вищеназваних факторів, ми приводимо спостереження, виконані з різних точок Землі у різний час, до одної системи, тобто редукуємо їх.
Астрономічна рефракція та її вплив на горизонтні координати світил.
Світло поширюється прямолінійно тільки у вакуумі та в абсолютно однорідному середовищі.
При переході з вакууму в матеріальне середовище з густиною |
|
або з одного матеріального |
середовища в інше різної густини промінь світла відхиляється від свого прямолінійного спрямування на деякий кут. Величина цього кута пропорційна густині матеріального середовища. Явище заломлення променів світла матеріальним середовищем, а також числову величину кута відхилення називають рефракцією.
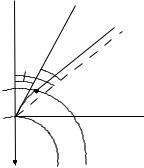
Атмосферною рефракцією називається заломлення променів світла земною атмосферою. Атмосферну рефракцію розділяють на земну і астрономічну. Земна рефракція, під якою розуміють заломлення атмосферою променів світла, що йдуть від земних предметів, вивчається в курсі вищої геодезії. Розглянемо астрономічну рефракцію, тобто заломлення земною атмосферою променів світла, що йдуть від небесних світил, та її вплив на координати світил. Атмосфера Землі є причиною того, що спостерігач бачить світило не там, де воно в дійсності знаходиться. Оскільки земна атмосфера є оптично неоднорідним середовищем, у якому густина збільшується від верхньої межі атмосфери до поверхні Землі, тому прямолінійний промінь, що йде від світила, буде поширюватися в атмосфері не прямолінійно, а за деякою кривою, зверненою опуклістю до прямовисної лінії. Внаслідок цього спостерігач, що знаходиться на земній поверхні в точці М (рис.
28), побачить світило не у напрямку прямої |
M , що з'єднує його око зі світилом, а в напрямку |
||||
дотичної |
M |
|
до кривої |
M , якою світловий промінь поширюється в атмосфері. Оскільки |
|
|
|||||
розміри земної атмосфери знехтувано малі у порівнянні з відстанями до небесних світил, тому
напрямок |
M 0 |
проведений паралельно до напрямку променя k . |
|||
|
|
Z |
|
` |
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
z` |
z |
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
M |
|
|
H |
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
O |
|
|
|
Рис. 28. Астрономічна рефракція.
