
Конспект лекцій Паляниця
.pdfВступ.
Астрономія є однією з найдавніших наук. Перші згадки про астрономічні спостереження датовані VIII в. до н.е. Однак, ще за 3 тисячі років до н. е. єгипетські жреці зафіксували, що розливи Нілу наступали після появи на сході однією з найяскравіших зірок Сиріуса. З таких спостережень вони з великою на ті часи точністю визначили тривалість тропічного року. У Стародавньому Китаї за 2 тисячі років до н.е. китайські астрономи могли пророкувати наступи сонячних і місячних затемнень завдяки їх постійним спостереженням руху Сонця і Місяця.
Фактично астрономія виникла з практичних потреб людини. Кочові племена при своїх мандрах навчилися орієнтуватися, використовуючи Сонце, Місяць і зірки. Хлібороби тих часів знали, що зміна пір року пов'язана із змінами висоти Сонця опівдні. Подальший розвиток людства викликав потребу у вимірі часу, а з ним і в складанні календарів. Усього цього досягали шляхом виконання спостережень небесних світил, які на початку виробляли без всяких інструментів і були низької точності. Такі спостереження стали передумовою появи науки про небесні тіла – астрономії.
З розвитком людського суспільства перед астрономією висувалися нові завдання, для вирішення яких потрібні були більш досконалі способи спостережень і більш точні методи розрахунків. Поступово стали створюватися найпростіші астрономічні інструменти і розроблятися математичні методи обробки спостережень.
Слід відзначити великий внесок у становлення астрономії астрономами Стародавньої Греції. Виконані ними спостереження небесних світил стали основою формування положень про просторове положення небесних світил і Землі із визначенням її форми і розмірів, а також систем вимірювання часу. У II ст. до н. е. давньогрецький астроном Гіппарх встановив нерівномірність руху Місяця і Сонця по відношенню до зірок, за спостереженням місячних затемнень визначив відстань до Місяця, створив перший зоряний каталог і ввів шкалу яскравості зірок – зоряних величин, яка використовується і сьогодні. До найбільш важливих винаходів Гіппарха відносять передрозрахунок рівнодень.
Великий внесок у розвиток астрономії зробив астроном і математик Клавдій Птолемей (II ст. н. е.). На підставі накопиченого попередніми астрономами досвіду і власних астрономічних спостережень він видав книгу, в якій привів опис небесної сфери, її основних кіл, виклав основні положення сферичної тригонометрії і її використання при проведенні обчислень, пов'язаних з виконаними вимірюваннями положень світил на небесній сфері, описав способи і результати визначення висот Сонця і їх змін протягом року із застосуванням гномона, навів дані про тривалість року і місяця.
В епоху середньовіччя астрономи займалися лише спостереженнями видимих рухів планет і узгодженням цих спостережень з прийнятою геоцентричної системою Птолемея. Розвиток в цей період астрономія отримала тільки в Середній Азії і на Кавказі завдяки існуванню таких видатних астрономів як Аль-Баттані ( 850-929 рр.) , Біруні ( 973-1048 рр.) , Улугбека ( 1394-1449 рр.) та інші.
Особливо швидко астрономія стала розвиватися в епоху великих географічних відкриттів XV-XVI ст. Подорожі через океан вимагали більш точних і більш простих методів орієнтування і обчислення часу. Розвиток торгівлі і мореплавання настійно вимагало вдосконалення астрономічних знань і, зокрема, теорії руху планет. Епоха середньовіччя ознаменувалася створенням великим астрономом М. Коперником (1473-1543) своєї геліоцентричної системи світу. Саме в цей час Земля була визнана як планета сонячної системи, що має добовий і річний рухи. Такого роду відкриття в астрономії та суміжних з нею науках стали передумовою в удосконаленні астрономічних інструментів методів і способів спостережень небесних світил. Так, Кеплером в 1609-1618 рр. були відкриті закони рухів планет, а в 1687 р. Ньютон опублікував закон всесвітнього тяжіння.
Нова астрономія отримала можливість вивчати не тільки видимі, але і дійсні рухи небесних тіл. Її нові успіхи в цій області увінчалися в середині XIX ст. відкриттям планети Нептун , а в наш час – розрахунком орбіт штучних небесних тіл.
Астрономія і її методи мають велике значення в житті сучасного суспільства. Питання, пов'язані з виміром часу і забезпеченням людства знанням точного часу, вирішуються тепер спеціальними лабораторіями – службами часу. Астрономічні методи орієнтування поряд з іншими методами, як і раніше, застосовуються в мореплаванні і в авіації, а в останні роки і в космонавтиці.
Складання географічних і топографічних карт, передвирахування періодів морських припливів і відливів, визначення сили тяжіння в різних точках земної поверхні з метою виявлення покладів корисних копалин у своїй основі мають астрономічні методи.
Все це в свою чергу сприяло розділенню астрономії на ряд розділів, одним з яких стала сферична астрономія. Саме у сферичній астрономії займалися розробкою питань встановлення співвідношень, які характеризують зміни умов спостереження світил у будь-якій точці Землі і в будь-який момент часу, використовуються формули сферичної тригонометрії. Усього цього досягають шляхом встановлення систем небесних координат і систем вимірювання часу. Це пов'язано зі спостереженнями небесних об'єктів, які беруть участь у видимому добовому русі небесної сфери.
Згадки про сферичну астрономію пов'язані з першими регулярними, але не високоточними вимірюваннями на небесній сфері, виконаними за багато тисячоліть до нашого часу у Вавилоні, Єгипті та Китаї. У ті часи було виявлено ряд циклічних, повторюваних небесних явищ, які стали основою для встановлення таких одиниць часу як доба, місяць, рік. Виявлення таких явищ пов'язані з вимірами видимих положень Сонця, Місяця і планет по відношенню, як на той час вважалося, нерухомих на небесній сфері зірок. Такого роду вимірювання на небесній сфері сприяли появі сферичної тригонометрії.
Положення небесного світила на небесній сфері при виконанні спостережень у будь-якому пункті земної поверхні називають видимим. Внаслідок малості розмірів Землі у порівнянні із відстанями до зірок їх координати називають геоцентричними, оскільки центр небесної сфери, а саме, положення спостерігача, ототожнюється з центром Землі. У цьому випадку, при визначенні координат зірок вибір центру системи координат не залежить від координат місця спостереження.
У разі виконання спостережень об'єктів сонячної системи з різних пунктів поверхні Землі їх видиме положення серед зірок буде різним. Ці зміни викликані тим, що відстані до зазначених об'єктів можна прирівняти до радіусу Землі. Координати небесних світил сонячної системи, які залежать від місця розташування пунктів спостереження, отримали назву топоцентричних.
Дослідження показали, що при добовому русі Землі положення початку координат змінюється незначно, а при річному русі по орбіті, просторове положення спостерігача змінюється до двох астрономічних одиниць ( 1 а. о. дорівнює 149507870,7 км). Ця зміна положення центру небесної сфери призводить до зміни видимих положень найближчих до Землі зірок. У цьому випадку йдеться про річні зміни геоцентричних координат зірок. Тому, при високоточних визначеннях їх координат необхідно отримувати геліоцентричні координати, віднесені до центра Сонця.
Важливість приведення координат спостережуваних небесних світил до якого-небудь центру сфери пов'язано з необхідністю обліку руху Землі, тобто отриманні координат, вільних від руху спостерігача.
При вивченні даної дисципліни студенти знайомляться з астрономічною термінологією, з новими фундаментальними поняттями, без знання яких неможливо зрозуміти сутність спостережуваних на небесній сфері явищ, отримують навички користування інформацією зоряних каталогів. Сферична астрономія є основою для подальшого вивчення таких розділів астрономії як астрометрія, небесна механіка, а також дисциплін, пов'язаних з астрономічними спостереженнями і вивченням фігури Землі – геодинаміка та геодезія.
Зв'язок сферичної астрономії і астрометрії проявляється в тому, що астрометрія займається вимірами координат небесних об'єктів для створення зоряних каталогів і визначеннями координат пунктів на земній поверхні.
Найбільш важливими питаннями курсу сферичної астрономії є:
1.Системи небесних сферичних координат і залежності між ними на основі формул сферичної тригонометрії.
2.Явища добового обертання небесної сфери.
3.Підбір небесних світил для виконання спостережень з урахуванням їх координат, широти пункту і часу спостережень.
4.Системи часу і зв'язки між ними.

5. Облік таких факторів як рефракція, паралакс, аберація, прецесія, нутація, що спотворюють результати спостережень небесних світил, виконаних з поверхні Землі за допомогою дослідження їх впливу на зміни положення небесних світил, земної і небесної системи координат.
Основні формули сферичної тригонометрії.
Сферичною тригонометрією називають розділ математики, що займається вивченням сферичних трикутників. Установимо основні залежності між елементами в косокутному сферичному трикутнику. Для цього розглянемо трикутник АВС (рис.4), розташований на поверхні сфери одиничного радіуса, з центром у точці О.
Проведемо через вершину С площину, перпендикулярну до радіуса ОА, та іншу площину, перпендикулярну до радіуса ОВ. Перша площина перетинає площину СОА по лінії СМ, а площину АОВ – по лінії МD. Друга площина перетинає площину СОВ по лінії СF, а площину АОВ – по лінії FD. Кожна з названих площин перпендикулярна до площини АОВ, а значить перпендикулярна до неї і лінія їх перетину CD. Отже, кути CMО, DMО, CFО і DFО – прямі кути. Кут CMD дорівнює сферичному куту A, а кут CFD – сферичному куту B; кути BОC, CОA і BОA відповідно рівні сторонам a, b і c трикутника ABC.
З прямокутного трикутника CОM, оскільки радіус сфери дорівнює одиниці, маємо:
OM cos b; CM sin b. |
(1.3) |
З урахуванням (1.3) з прямокутного трикутника CMD маємо: |
|
CD sin b sin A, |
(1.4) |
DM sin bcos A. |
(1.5) |
З іншого боку, з прямокутних трикутників СОF і CFD: |
|
OF cos a, |
(1.6) |
CD sin a sin B, |
(1.7) |
DF sin a cos B. |
(1.8) |
|
|
|
|
C |
|
|
|
|
|
|
a |
|
|
|
|
|
b |
|
b |
a |
|
F |
|
O |
c |
|
B |
||
|
|
|
|||
|
|
|
|
|
|
|
|
|
M |
D |
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
A |
|
O |
L |
F |
c |
|
|
|
|
|
|
H |
D |
|
c |
|
|
M |
|
Рис. 4. До виведення формул сферичної Рис. 5. Чотирикутник OFDM в плані тригонометрії
На рис. 5 чотирикутник OFDM показаний в плані на площині ВОА. В цьому чотирикутнику проведемо лінію ML паралельно лінії DF і лінію DH паралельно лінії ОF. Результатом цих побудов є утворення прямокутних трикутників ОLM і DHM. Кут DMH дорівнює кутові MОL тому, що це кути з перпендикулярними сторонами. Оскільки кут MОL дорівнює кутові с, то і кут DMH також дорівнює кутові c. Очевидно, що:
OF OL LF OM cos c DM sin c, |
(1.9) |
DF ML MH OM sin c DM cosc. |
(1.10) |
Одна з формул для розв’язання сферичного трикутника називається формула косинуса сторони та має формулювання: у всякому сферичному трикутнику косинус будь-якої сторони дорівнює добутку косинусів двох інших сторін плюс добуток синусів тих же сторін на косинус
кута між ними |
|
cosa cosbcosc sin bsin ccos A. |
(1.11) |
Ця формула пов'язує між собою три сторони і один з кутів сферичного трикутника.

Доведення. При заміні в рівнянні (1.9) літерних позначень рівняннями (1.3), (1.5) і (1.6), отримаємо рівняння (1.11), що й необхідно було довести. Аналогічно доводяться і записуються формули для інших сторін трикутника.
Для розв’язання сферичного трикутника існує ще одна формула, яка має назву формули синусів та наступне формулювання: у всякому сферичному трикутнику добуток синуса будь-якої сторони на синус прилеглого кута дорівнює добутку синусів протилежних елементів
sin asin B sin bsin A. |
(1.12) |
Ця формула пов'язує між собою протилежні елементи трикутника – кути і сторони. Доведення. У результаті прирівняння правих частин рівнянь (1.4) і (1.7), отримаємо рівняння
(1.12), що й необхідно було довести. Аналогічно записують формулу для інших пар елементів трикутника (сторони і прилеглого кута):
sin b sin C sin c sin B,
sin c sin A sin a sin C.
Перегрупувавши члени в цих рівняннях, отримаємо
sin a |
|
sin b |
|
sin c |
k. |
(1.13) |
|
sin A |
sin B |
sin C |
|||||
|
|
|
|
З останнього рівняння можна зробити висновок: у всякому сферичному трикутнику синуси сторін пропорційні синусам протилежних кутів і їхнє відношення є сталою величиною для даного трикутника. Формула синусів застосовується для обчислення одного з елементів, що входить у вказані рівняння, якщо відомі три інших.
Наступною формулою для розв’язання сферичного трикутника є формула п'яти елементів,
яка має формулювання: у всякому сферичному трикутнику синус будь-якої сторони, помножений на косинус прилеглого кута, дорівнює косинусу протилежної сторони цьому куту, помноженому на синус третьої сторони, мінус синус протилежної сторони цьому куту, помножений на косинус третьої сторони і на косинус кута, протилежного першій стороні
sin acos B sin ccosb coscsin bcos A.
(1.14)
Ця формула пов'язує п'ять елементів сферичного трикутника – три сторони і два кути. Доведення. Замінимо в рівнянні (1.10) літерні позначення рівняннями (1.3), (1.5), (1.8) і
отримаємо рівняння (1.14), що й потрібно було довести. Для інших комбінацій кутів і сторін у сферичному трикутнику можна отримати ще п'ять аналогічних рівнянь.
Ще одною формулою для розв’язання сферичного трикутника є формула чотирьох елементів або формула котангенсів: у всякому сферичному трикутнику котангенс крайнього кута, помножений на синус середнього кута, дорівнює котангенсу крайньої сторони, помноженому на синус середньої сторони, мінус добуток косинусів середніх елементів (сторони і кута)
ctgAsin B ctgasin c cos c cos B.
(1.15)
Ця формула пов'язує чотири поруч елементи сферичного трикутника, наприклад, елементи А, с, В, а. Назвемо два елементи кут A і сторону a крайніми елементами, а інші два елементи сторону c і кут B середніми елементами (рис. 6).
Доведення. Візьмемо формули (1.12) і (1.14) для одних і тих же сторін і кутів у лівих частинах рівнянь, наприклад, для сторони b і кута A :
sin b sin A sin a sin B,
sin b cos A sin c cos a cos c sin a cos B.
Розділивши друге рівняння на перше, отримаємо:
ctgA sin c ctga cos c cos B , sin B
звідки отримаємо рівняння (1.15), що і необхідно було довести.
Аналогічно може бути написано ще п'ять таких рівнянь для інших поєднань чотирьох суміжних елементів. Формула котангенсів застосовується для обчислення сторони або кута трикутника, якщо вони лежать поруч з трьома відомими елементами.

A
c
b
B
a
C
Рис. 6. Суміжні елементи сферичного трикутника Наступною формулою для розв’язання сферичного трикутника є формула косинуса кута із
формулюванням: у всякому сферичному трикутнику косинус будь-якого кута дорівнює добутку косинусів двох інших кутів зі знаком «мінус» плюс добуток синусів тих же кутів на косинус сторони, прилеглої до них.
cos A cos BcosC sin Bsin C cos a. |
(1.16) |
Ця формула пов'язує між собою три кути і одну зі сторін сферичного трикутника і приводиться тут без доведення.
У разі розв'язку прямокутних сферичних трикутників формули (1.11) – (1.16) стають одночленними, що прискорює обчислення. Для зручності запам'ятовування таких перетворених основних формул розв'язку прямокутних трикутників (рис. 7) існує наступне мнемонічне правило Непера-Модюі: якщо катети прямокутного сферичного трикутника замінити їх доповненнями до 90° і не враховувати прямого кута, то косинус будь-якого шуканого елемента дорівнює добутку котангенсів суміжних з ним елементів, або добутку синусів несуміжних з ним елементів.
|
C |
|
|
b |
|
|
90°-b |
|
|
a |
|
|
A |
|
|
c |
|
B |
90°-c |
|
Рис. 7. Прямокутний сферичний трикутник (до правила Непера-Модюі) |
|
|
Наприклад, |
|
|
|
cos a ctgB ctgC, |
(1.17) |
cos a sin( 90 b)sin( 90 c) cosbcosc, |
(1.18) |
|
|
cos C ctga ctg(90 b) ctgatgb, |
(1.19) |
cosC sin Bsin( 90 c) sin B cos c, |
(1.20) |
|
cos(90 |
b) ctgCctg(90 |
c |
|
|
|
|
cos(90 b) sin asin |
|
|
|
|
) ctgCtgc sin b, B sin b.
(1.21)
(1.22)
Аналогічно, за формулами (1.19) – (1.22), користуючись мнемонічним правилом НепераМодюі, можна встановити залежності для знаходження елементів B і c .

Небесна сфера
Для визначення положення небесного світила σ можна використовувати дві системи координат: просторову прямокутну з координатами X, Y, Z та полярну з координатами α, β, R (рис. 8). Для названих систем координат початок координат – точка О і напрям осей можна задавати за заданими вихідними даними.
Z
|
|
|
|
|
R |
|
|
Z |
O |
Y |
|
|
|
|
|
|
X |
|
Y |
|
X
Рис. 8. Прямокутна просторова і полярна системи координат
В прямокутній просторовій системі координат положення світила σ визначається трьома лінійними координатами X, Y, Z. У цьому випадку відстань від світила σ до точки О обчислюється за формулою
R 
 X 2 Y 2 Z 2 . (2.1)
X 2 Y 2 Z 2 . (2.1)
У полярній системі координат положення світила σ задається однією лінійною координатою
– радіусом-вектором R = Oσ і двома кутовими: кутом між віссю X і проекцією радіуса-вектора R на координатну площину XOY і кутом між координатною площиною XOY і радіусомвектором R . Зв'язок прямокутних і полярних координат описується формулами:
X R cos cos , |
||
|
|
|
Y R cos sin , |
||
Z R sin . |
|
|
|
||
|
||
(2.2)
Ці системи використовуються в тих випадках, коли лінійні відстані R до небесних світил відомі (наприклад, для Сонця, Місяця, планет, штучних супутників Землі тощо). Однак для багатьох світил, які спостерігаються за межами Сонячної системи, ці відстані або надзвичайно великі у порівнянні з радіусом Землі, або невідомі.
При вивченні видимих рухів небесних світил необхідно із заданою точністю визначати їх положення на моменти спостережень. При цьому відстані до них можуть бути невідомими, оскільки всі вони представляються нам як такими, що знаходяться на поверхні деякої сфери. Тому видимі положення небесних світил можна визначати тільки напрямками на них, а їх взаємне розташування – кутами між цими напрямками або відповідними дугами великих кіл на сфері, з центру якої виходять усі ці напрямки. Уявна сфера довільного радіуса з центром у довільній точці простору, на поверхні якої розташовані світила у їх видимому на небосхилі положенні в деякий момент часу із даної точки простору, називається допоміжною небесною сферою. Центром цієї

уявної сфери є спостерігач, який разом з Землею приймає участь в її добовому і річному рухах. При цьому, добове обертання допоміжної небесної сфери повторює обертання небозводу.
На допоміжну небесну сферу проектується зображення небесних світил (рис. 9). При цьому передбачається, що спостерігач знаходиться в центрі цієї сфери, а спостережуване небесне світило знаходиться на небесній сфері в точці, в якій лінія, що прямує від спостерігача до цього світила σ, перетинає сферу. Тому під положенням небесних світил в астрономічних сферичних системах координат розуміється не їх істинне розташування в просторі, а ті місця, які вони займають на небесній сфері. Таким чином, положення будь-якого небесного світила на такій небесній сфері визначається за допомогою двох сферичних координат і :
X cos cos , |
||
|
|
|
Y cos sin , |
||
Z sin . |
|
|
|
||
|
||
|
|
|
2 |
|
|
1 
 3
3
R
O
(2.2`)
Рис. 9. Побудова допоміжної небесної сфери У залежності від місця розташування центру небесної сфери О, розрізняють:
●топоцентричну небесну сферу – центр знаходиться на поверхні Землі;
●геоцентричну небесну сферу – центр збігається з центром мас Землі;
●геліоцентричну небесну сферу – центр суміщений з центром мас Сонця;
●барицентричну небесну сферу – центр знаходиться в центрі ваги Сонячної системи;
●планетоцентричну небесну сферу – центр знаходиться в центрі якоїсь планети.
Основні кола, точки та лінії небесної сфери
Небесна сфера служить для вивчення видимих положень і рухів небесних тіл. Для цього на її поверхні фіксуються основні лінії і точки, по відношенню до яких проводяться відповідні вимірювання. Встановлення системи небесних координат, основних кіл і точок небесної сфери та основних напрямків пов'язано з наступними явищами: напрямком дії сили тяжіння Землі, явищем добового обертання Землі – видимим добовим обертанням небесної сфери, річним рухом Землі навколо Сонця – річним рухом Сонця по небесній сфері з видимим рухом Сонця щодо зірок.
Основні кола, точки і лінії небесної сфери зображені на рис. 10. Одним з основних напрямків щодо поверхні Землі є напрямок прямовисної лінії або сили тяжіння в точці спостереження. Цей
напрямок перетинає небесну сферу у двох діаметрально протилежних точках – |
Z |
і Z . Точка |
Z |
знаходиться над центром і називається зенітом, |
Z |
|
– під центром і називається надиром. Через |
|
центр небесної сфери проведемо лінію і площину, перпендикулярні прямовисній лінії ZZ . Проведена таким чином лінія перетинається з небесною сферою в двох точках N – точка півночі і S – точка півдня, а площина утворює у перетині зі сферою велике коло, що називається небесним (істинним) або астрономічним горизонтом. Ця побудова є основною площиною топоцентричної системи координат. Пряма NS називається полуденною лінією. Якщо в площині небесного
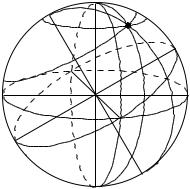
горизонту побудувати лінію перпендикулярну полуденній лінії і таку, що проходить через центр сфери О, то ця лінія перетне небесну сферу в двох точках E – точка сходу і W – точка заходу. Точки S, W, N, E називаються головними точками горизонту. Небесний горизонт розділяє небесну сферу видиму півсферу, в якій розташований зеніт, і не видиму з точкою надира.
Пряма |
PN PS , проведена |
через центр небесної сфери паралельно осі обертання Землі, |
називається віссю світу. Точка |
PN називається північним полюсом світу, точка PS – південним |
|
полюсом світу. Навколо осі світу відбувається видимий добовий рух небесної сфери. Проведемо
через центр сфери площину, перпендикулярну осі світу |
|
|
|
|
PN PS . Велике коло QWQ E , утворене в |
||||
результаті перетину |
цією площиною небесної сфери, |
називається небесним (астрономічним) |
||
екватором. Точка Q |
цього кола називається верхня точка екватора (над горизонтом), Q |
|
– нижня |
|
|
||||
точка екватора (під горизонтом). Небесний екватор і небесний горизонт перетинаються в точках W і E . Небесний екватор розділяє небесну сферу на північну півкулю з північним полюсом світу і південну – з південним полюсом світу.
|
|
|
Z |
|
|
q |
|
|
|
|
|
n |
P |
|
|
|
|
|
|
|
|
|
N |
|
|
s |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
q` |
|
|
|
|
|
|
|
|
|
|
N |
|
O |
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
Q` |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
Z` |
|
|
|
|
|
|
|
Рис. 10. Основні кола, точки та лінії небесної сфери |
|
|
||||||||
Площина, що містить точки |
|
|
|
, |
прямовисну лінію |
ZZ |
|
і вісь світу |
PN PS , |
|
PN ZQSPS Z Q N |
|
|||||||||
називається істинним (небесним) або астрономічним меридіаном. Ця площина паралельна площині земного меридіана та перпендикулярна до площини горизонту і екватора. Її називають початковою координатною площиною. Небесний меридіан розділяє небесну сферу на східну півсферу, в якій небесні світила сходять, і західну – в якій світила заходять.
Прямовисна лінія ZZ ділить небесний меридіан на південну частину ZPS Z , яка вміщує південний полюс миру, та північну частину ZPN Z , яка вміщує північний полюс миру. Вісь світу PN PS ділить небесний меридіан на верхню частину меридіана PN ZPS , яка вміщує точку зеніту Z та нижню частину PN Z PS , яка вміщує точку надиру Zʹ.
Проведемо через прямовисну лінію |
ZZ |
|
вертикальну площину, перпендикулярну небесному |
|
меридіану. Отримане коло ZWZ E називається першим вертикалом.
Велике коло Z Z , утворене в результаті перетину небесної сфери площиною, що проходить через світило та точки Z і Z', називається вертикалом або колом висот світила.
Велике коло PN PS , що проходить через світило перпендикулярно небесному екватору,
називається колом схилення світила.
Мале коло s n , що проходить через світило паралельно небесному горизонту, називається колом рівних висот або альмукантарат.
Мале коло , що проходить через світило і є паралельним небесному екватору,
називається добовою паралеллю світила. Видимий добовий рух світил відбувається уздовж добових паралелей. Точка q добової паралелі називається точкою верхньої кульмінації, точка q' – точкою нижньої кульмінації. У точці верхньої кульмінації світило має максимальне значення висоти над горизонтом, у точці нижньої кульмінації – мінімальне.
У першому наближенні орбіта Землі може бути прийнята за плоску криву – еліпс, в одному з фокусів якого знаходиться Сонце. Площина еліпса, прийнятого за орбіту Землі, називається площиною екліптики E E (рис. 11).

У сферичній астрономії прийнято говорити про видимий річний рух Сонця. Велике коло
|
за яким відбувається річний рух Сонця на протязі року, називається екліптикою. Точка Е |
E E |
цього кола називається точкою літнього сонцестояння, Еʹ – точка зимового сонцестояння. Якщо через центр сфери провести лінію перпендикулярну до площини екліптики, то вона перетне
небесну сферу в двох точках |
RN – північний полюс екліптики і |
RS – південний полюс екліптики. |
Лінію RN RS називають вісь |
екліптики. Площина екліптики |
нахилена до площини небесного |
екватора на кут ε, наближено рівний 23,5º. Велике коло небесної сфери RN RS , яке проходить через полюси екліптики і через світило σ, називається колом широти світила.
|
|
P |
|
|
|
|
R |
N |
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
Q` |
|
O |
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E` |
|
|
|
|
|
|
|
P |
|
R |
S |
|
|
|
|
||
|
|
|
|
|
|
|
|
S |
|
|
|
Рис. 11. Кола і точки небесної сфери, пов'язані з видимим річним рухом Сонця |
|||||
Зі спостережень зірок у їх видимому добовому русі визначається положення небесного екватора. Зі спостережень тих самих зірок і, разом з ними, Сонця у його добовому і річному рухах визначається величина нахилу екліптики до небесного екватора і положення точок перетину екліптики з небесним екватором, які називають точками рівнодення. На рис. 11 ці точки показані
як: |
|
– точка весняного рівнодення, |
|
– точка осіннього рівнодення. В точці весняного |
рівнодення Сонце знаходиться в момент перетину ним небесного екватора при переході з південної півкулі у північну у видимому річному його русі. У такому положенні Сонце знаходиться 21 березня. 23 вересня Сонце здійснює перехід з північної півкулі у південну – проходить точку осіннього рівнодення. В момент знаходження Сонця в точці Е (22 червня) в північній півкулі Землі день має найбільшу тривалість, а ніч – найменшу. 22 грудня Сонце знаходиться в точці Еʹ, в цей момент в північній півкулі Землі день має найменшу тривалість, а ніч
– найбільшу.
Системи небесних сферичних координат
Положення небесного світила або будь-якої точки на небесній сфері однозначно визначається по відношенню до основних площин та пов'язаних з ними лініями і точками небесної сфери. У кількісному відношенні воно задається двома величинами – центральними кутами або дугами великих кіл, які називаються сферичними координатами.
Для визначення сферичних координат на сфері вибирають два взаємно перпендикулярних великих кола, одне з яких називають основним, а інше – початковим колом системи. Дуги цих кіл будуть представляти собою лінії положень небесного світила на небесній сфері. При цьому, одна з точок перетину цих кіл називається початковою точкою системи. Із сферичної тригонометрії відомо, що положення великого кола вважається визначеним, якщо відоме положення геометричного полюса цього кола. Геометричним полюсом великого кола є точка сфери, яка знаходиться на кутовій відстані у 90° від всіх точок цього кола. Якщо провести велике коло через геометричні полюси даної системи координат і небесне світило, отримаємо визначальне коло цієї системи.
Перелічені кола і точки покладені в основу опису всіх сферичних систем координат. Для графічного представлення кожної із сферичних систем координат застосовують наступну послідовність дій. Через полюси системи і небесне світило проводять визначальне коло. Першою

координатою системи вважають дугу проведеного кола від основного кола до небесного світила. Друга координата відраховується від початкової точки по основному колу до точки перетину визначального та основного кола.
У геодезичній астрономії використовуються декілька систем сферичних координат, що різняться між собою вибором основного та початкового кола, початкової точки та напрямом відліку координат. До найбільш застосовуваних відносять наступні системи сферичних координат:
1)горизонтна,
2)перша і друга екваторіальні,
3)екліптична,
4)географічна.
Назва перших трьох систем відповідає назві великих кіл, прийнятих за основне. Розглянемо ці системи координат докладніше.
Горизонтна система координат
Основні елементи горизонтної системи координат показані на рис. 12. Основним колом цієї
системи є астрономічний горизонт SWNE. Початкове коло системи – небесний меридіан |
|
|||
ZSZ N . |
||||
Геометричними полюсами цього кола є Z (зеніт) і Z |
|
(надир). Початкова точка системи – точка |
||
|
||||
півдня S . Визначальне коло системи – вертикал світила Z Z . |
|
|||
Перша координата горизонтної системи – висота |
h |
світила, тобто кут MO між площиною |
||
горизонту і напрямком на світило, або дуга вертикала |
M від горизонту до світила. |
Висота |
||
відраховується від горизонту і може приймати значення від 0° до +90°, якщо світило знаходиться над горизонтом або від 0° до -90°, якщо світило знаходиться під горизонтом. Іноді замість висоти h використовується зенітна відстань z світила – кут ZO між прямовисною лінією і напрямком на світило або дуга вертикала Z . Зенітна відстань є доповненням висоти h до 90º:
z 90 |
|
|
h
.
(2.3)
Зенітна відстань світила відраховується від зеніту і може приймати значення від 0° до 180°.
Паралельно небесному горизонту через світило |
|
проведемо мале коло s n . Характерною |
ознакою цього кола є умова: h = const. Це коло називається колом рівних висот або альмукантарат.
|
Z |
A |
|
|
|
|
|
|
|
|
|
z |
|
|
|
n |
|
|
s |
|
|
|
|
|
|
E |
|
h |
|
|
z |
|
|
|
N |
h |
A |
|
S |
O |
|
|||
|
|
|
||
|
W |
|
M |
A |
|
|
|
Z`
Рис. 12. Горизонтна система координат Друга координата горизонтної системи азимут
небесного меридіана (дуга початкового кола ZSZ ) і
A SOM SM сф.кут SZM .
A світила площиною
– двогранний кут між площиною вертикала Z Z світила:
В астрономії азимути відраховують від точки півдня S за годинниковою стрілкою в межах від 0° до 360°.
Внаслідок добового обертання небесної сфери горизонтні координати світила змінюються протягом доби. Тому, фіксуючи положення світил у цій системі координат, потрібно визначати момент часу, до якого відносяться координати h , z і A . Крім того, горизонтні координати
