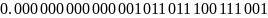БДЗ1_ЧМ

Никитиной Софии

ИВТ-24

БДЗ №1

1. Рассмотрим число 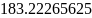. В формуле 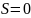, т.к. знак положителен. Представим числа в двоичной системе счисления – преобразуем целые и дробные части:

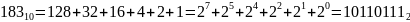
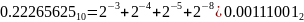
0.22265625	0
0.4453125	0
0.890625	1
0.78125	1
0.5625	1
0.125	0
0.25	0
0.5	1

183	1
91	1
45	1
22	0
11	1
5	1
2	0
1	1

Складывая целую и дробную части, получим, что

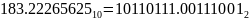
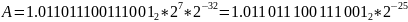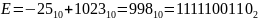Нормализуем число, учитывая множитель и знак: Бит знака Показатель степени (10 бит) Мантисса 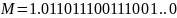(52 бита +1 для ведущей единицы)

Имеем:

0	1111100110	(1.)0110111001111001..0
S	E	M

2. Рассмотрим число 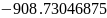. В формуле 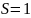, т.к. знак отрицателен.

Аналогично преобразовываем числа:

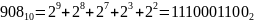
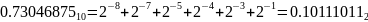
Получим, что

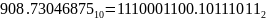
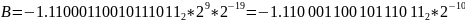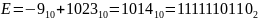Нормализуем число, учитывая множитель и знак: Бит знака Показатель степени (10 бит) Мантисса 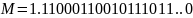(52 бита +1 для ведущей единицы)

Имеем:

1	1111110110	(1.)11000110010111011..0
S	E	M

Сложим числа: 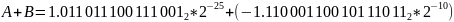Разница между порядками чисел равна -25+(-10)=-15 , значит расстояние между началами складываемых мантисс 15-1=14 бит. Отведенных на это 52 бита хватает, следовательно, погрешность не указывается. При сложении чисел в машинном вычислении меньшее число приводится к порядку большего. К А спереди прибавляется 15 нулей.

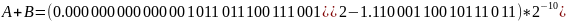
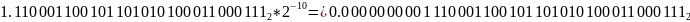
НО: Так как из меньшего вычиталось большее, ставим отрицательный знак. 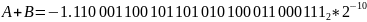Или в десятичном виде:

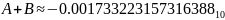
function Output=BDZ1(n)

Powers1=repmat([1:1:n],1,1)

Powers2=repmat([0:1:n-1]',1,n)

Powers=Powers1+Powers2

Output=exp(1./Powers);

end

Пусть n=4.

>>BDZ1(4)

Powers1=repmat([1:1:n],1,1) – создаем вектор-строку размерностью n

Powers1 =

1 2 3 4

Powers2=repmat([0:1:n-1]',1,n) – а так же создаем матрицу из разности входящих в нее чисел

Powers2 =

0 0 0 0

1 1 1 1

2 2 2 2

3 3 3 3

Powers=Powers1+Powers2 – складываем нашу исходную матрицу с матрицей разницы

Powers =

1 2 3 4

2 3 4 5

3 4 5 6

4 5 6 7

Output=exp(1./Powers); – возводим экспоненту в готовые степени, реализуя функцию 1/n

ans =

2.7183 1.6487 1.3956 1.2840

1.6487 1.3956 1.2840 1.2214

1.3956 1.2840 1.2214 1.1814

2840. 1.2214 1.1814 1.1536

Для локализации корней используем метод перебора

f=@(x)x^4+5*x^3-x^2+2;

a=-10000;

b=10000;

h=0.05;

for i=a:h:b

if f(i)*f(i-h)<0

sprintf('Roots are on: [%f, %f]',i-h,i)

end

end

'Roots are on: [-5.20000, -5.150000]'

'Roots are on: [-0.750000, -0.700000]' Из этого мы можешь сделать вывод, что существует 2 вещественных корня.

1. Чтобы найти первый корень, используем итерационный процесс к нему сходящийся. В данном случае метод Ньютона :

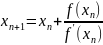
Возьмём в качестве начального приближения начало интервала, на котором был обнаружен корень: -5.2.

eps=0.001;

x0=-5.2;

f=@(x)x^4+5*x^3-x^2+2;

diff=@(x)4*x^3+15*x^2-2*x;

x1=x0-(f(x0)/diff(x0));

x2=x0;

while (((x1-x0)^2)/abs(2*x0-x1-x2))>eps

x2=x0;

x0=x1;

x1=x0-(f(x0)/diff(x0));

end

x1

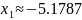
2. Чтобы найти второй корень, используем итерационный процесс к нему сходящийся. В данном случае метод Ньютона:

Возьмём в качестве начального приближения начало интервала, на котором был обнаружен корень: -0.75.

eps=0.001;

x0=-0.75;

f=@(x)x^4+5*x^3-x^2+2;

diff=@(x)4*x^3+15*x^2-2*x;

x1=x0-(f(x0)/diff(x0));

x2=x0;

while (((x1-x0)^2)/abs(2*x0-x1-x2))>eps

x2=x0;

x0=x1;

x1=x0-(f(x0)/diff(x0));

end

x1

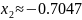
Тогда итерационный процесс Ньютона представлен, как:

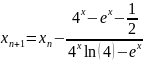
Возьмём в качестве начального приближения границу [0.5;1].

Найдём вторую производную:

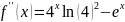
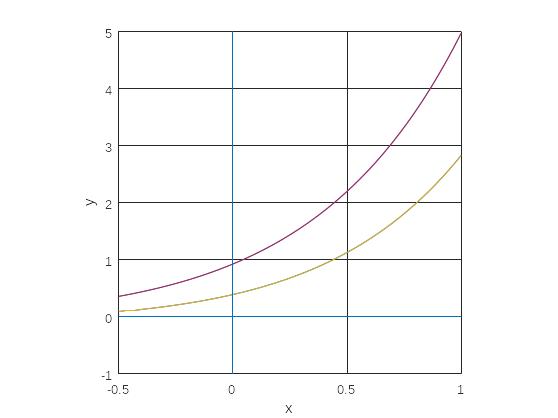
Построим график для наблюдения знаков производных:

Из построенного графика видно, что

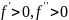
Согласно теореме для того, чтобы 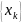монотонно убывала и сходилась к 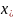необходимо выбрать

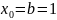
Решением является

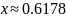
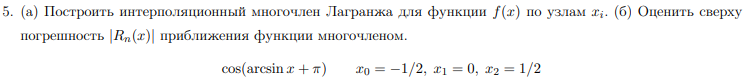
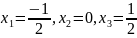
Построим интерполяционный многочлен Лагранжа:

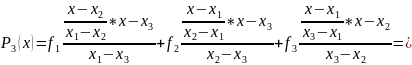
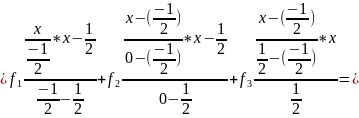
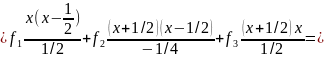
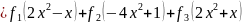
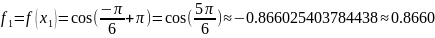
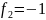
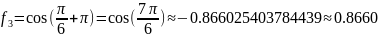
Раскрыв скобки и подставив 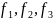получим:

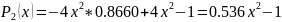
Оценим погрешность, исследовав выражение

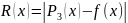
Найдём производную

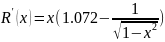
Приравняем к нулю и решим.

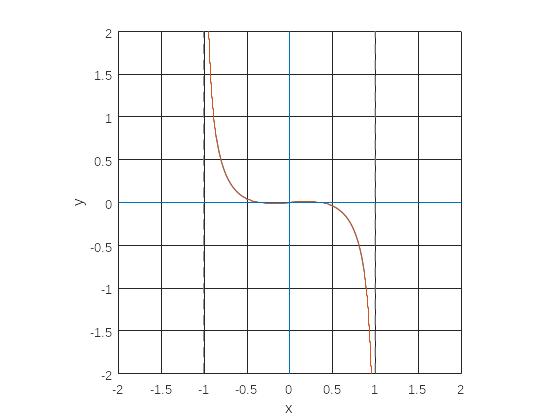
Аналитически и графически мы можем видеть, что нужный корень 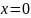. Делаем вывод, что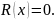

а) Погрешность интерполяции можно рассчитать по формуле:

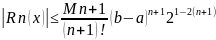
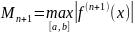, где n - степень многочлена, (n+1) – кол-во чебышёвских узлов.

Пусть n=4, тогда

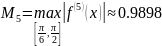
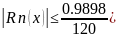
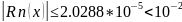
Значит для заданной точности нам будет достаточно 4 узла.

Найдём корни полинома Чебышева 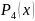, пока что на отрезке [-1,1]

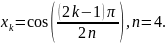
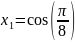
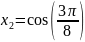
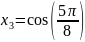
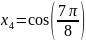
Т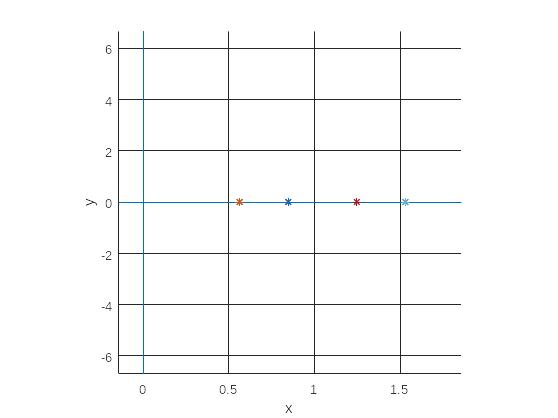 еперь используем линейное отображение 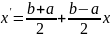, для получения чебышевских узлов на заданном в условии промежутке. Отметим их на действительной оси Ох

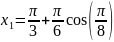
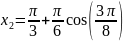
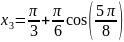
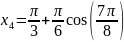
Построим аппроксимирующий многочлен первой степени.

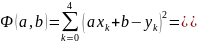
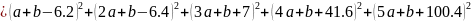
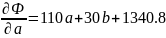
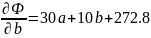
Приравняем частные производные к нулю и решим систему уравнений:

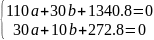
Получаем

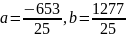
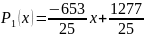
Построим аппроксимирующий многочлен второй степени.

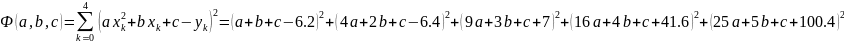
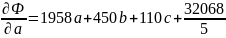
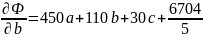
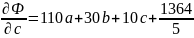
Приравняем частные производные к нулю и решим систему уравнений:

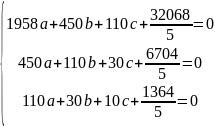
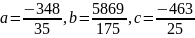
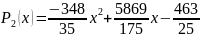
Построим аппроксимирующий многочлен третьей степени.

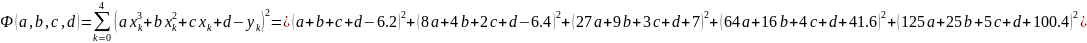
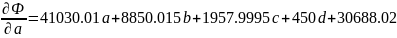
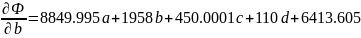
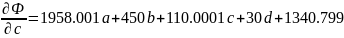
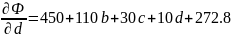
Приравняем частные производные к нулю и решим систему уравнений:

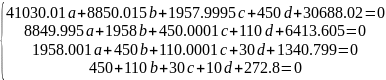
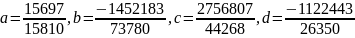
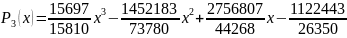
Найдём среднеквадратичное отклонение для каждого многочлена:

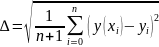
Для

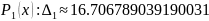
Для

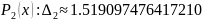
Для

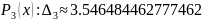
С.К.О. минимально для многочлена второй степени. Значит в данном эксперименте наиболее вероятна квадратичная зависимость.

Приблизим функцию y(x) многочленом Лагранжа по узлам

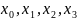
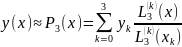
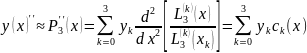
Значение 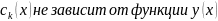и по условию нам необходимо найти 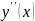, тогда заменим

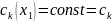
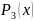точно приближает функции

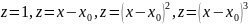
Найдём производные второго порядка от функций z:

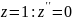
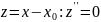
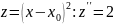
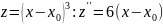
Подставляем последовательно соотношения и соответственно в правую и левую части, при 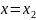требуя выполнения точного равенства:

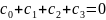
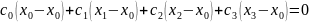
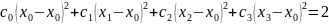
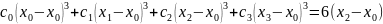
Запишем расстояние между узлами:

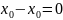
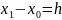
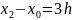
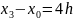
Получаем окончательно систему уравнений в виде:

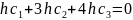
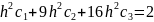
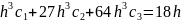
Решая эту систему, получаем:

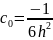
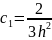
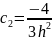
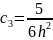
Получаем:

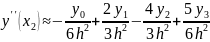
Теперь определим порядок погрешности в полученной формуле.

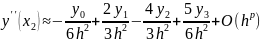
Разложим 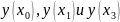в ряд Тейлора в окрестностях точки 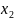до члена

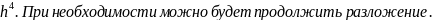
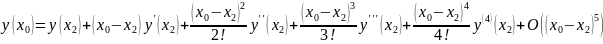
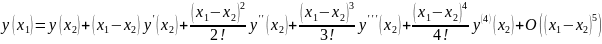
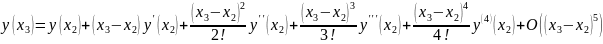
Сократим запись, учитывая расстояние между узлами.

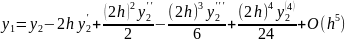
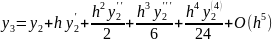
Подставив эти значения в формулу , получим:

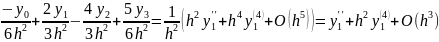
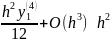, значит порядок погрешности полученной в первой части задания формулы равен двум.