Правило 3:

3) базисная переменная, отвечающая строке разрешающего элемента, должна быть переведена в разряд свободных, а свободная переменная, отвечающая столбцу разрешающего элемента, вводится в число базисных. Строится новая таблица, содержащая новые названия базисных переменных: ведущий (разрешающий) элемент заменяется на обратное число с тем же знаком, элементы ведущей строки делятся на ведущий элемент, элементы ведущего столбца делятся на ведущий элемент и меняют свой знак.

базисные переменные	x1	y2	y3	свободные члены
y1	1	2	0	7
x2	1,6	6	0	8
x3	1,3	0	1	6
L	6	-5	0	54

Правило 4:

Разрешающий элемент Р=6. Строка, соответствующая переменной x₂ , получена в результате деления всех элементов строки x₂ на разрешающий элемент РЭ=6 На месте разрешающего элемента получаем 1. В остальных клетках столбца y₂ записываем нули. Все остальные элементы определяются по правилу прямоугольника. Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент Р. НЭ = СЭ - (А*В)/Р СЭ - элемент старого плана, Р - разрешающий элемент (6), А и В - элементы старого плана, образующие прямоугольник с элементами СЭ и Р. Представим расчет каждого элемента в виде таблицы:

1-(-1.6 • 2):6	2-(6 • 2):6	0-(0 • 2):6	7-(8 • 2):6
1.6 : 6	6 : 6	0 : 6	8 : 6
1.3-(-1.6 • 0):6	0-(6 • 0):6	1-(0 • 0):6	6-(8 • 0):6
6-(-1.6 • -5):6	-5-(6 • -5):6	0-(0 • -5):6	54-(8 • -5):6

базисные переменные	x1	y2	y3	свободные члены
y1	1,5	0	0	4,3
x2	0,2	1	0	1,3
x3	1,3	0	1	6
L	4,6	0	0	60,6

Т.к. все элементы заключительной строки оказались положительными, то мы достигли максимума. Оптимальное решение содержится в заключительном столбце, а именно: y₁=4,3, x₂=1,3, x₃=6

Таким образом, оптимальный план будет:

x₁=0; y₁=4,3; y₂=0; x₂=1,3; y₃=0; x₃=6;

Оптимальное значение максимизируемой функции L=60,6

Найдем наименьшее значение линейной функции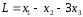

при следующих ограничениях

Решение :

Умножим коэффициенты исходной функции на -1. (и ищем максимум)

Будем искать наибольшее значение получившийся функции. Обратите внимание, что максимальное значение рассматриваемой функции равно наименьшему значению исходной функции по модулю, но значения противоположны по знаку. Другими словами, получившийся ответ мы должны будем умножить на -1.

Нам необходимо найти начальное опорное (абсолютно произвольное) решение для функции G, которое бы удовлетворяло системе наложенных ограничений. Далее, применяя симплекс таблицы, мы будем получать решения, при которых значение функции будет, как минимум, не убывать. И так до тех пор, пока не достигнем оптимально решения, при котором функция достигает своего максимума. Перед применением симплекс таблиц, необходимо преобразовать систему линейных ограничений и рассматриваемую нами функцию G к вполне определенному виду.

Свободные члены системы ограничений должны быть неотрицательными.

Умножим коэффициенты ограничения 2 на -1, свободный член ограничения станет положительным.

Свободные члены системы ограничений неотрицательные.

Система ограничений должна быть приведена к каноническому виду:

К левой части неравенства 1 системы ограничений прибавляем неотрицательную переменную y₁ - преобразуем неравенство 1 в равенство.

К левой части неравенства 2 системы ограничений прибавляем неотрицательную переменную y₂ - преобразуем неравенство 2 в равенство.

К левой части неравенства 3 системы ограничений прибавляем неотрицательную переменную y₃ - преобразуем неравенство 3 в равенство.

Система ограничений приведена к каноническому виду, т.е. все условия системы представляют собой уравнения.

Определимся с начальным опорным решением.

Наличие единичного базиса в системе ограничений позволяет легко найти начальное опорное решение. Рассмотрим подробнее:

Переменная y₁ входит в уравнение 1 с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е. y₁ - базисная переменная.

Переменная y₂ входит в уравнение 2 с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е. y₂ - базисная переменная.

Переменная y₃ входит в уравнение 3 с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е. y₃ - базисная переменная.

Переменные, которые не являются базисными называются свободными переменными. Приравняв свободные переменные нулю в получившийся системе ограничений мы получим начальное опорное решение.

X _нач = ( 0 , 0 , 0 , 3 , 6 , 15 )

Вернемся к рассмотрению функции G.

Функция G не содержат базисных переменных.

Для составления начальной симплекс таблицы мы выполнили все условия.

В процессе дальнейших преобразований возможны два случая. Если в симплекс таблице, на каком то шаге, мы получим строку G состоящую из неотрицательных элементов - задача решена, мы нашли оптимальное решение. В противном случае - функция не является ограниченной.

Обратите внимание:

При составлении исходной симплекс таблицы, коэффициенты при переменных функции G записываются с противоположными знаками, а свободный член со своим знаком.

Правило 1:

1. в качестве разрешающего выбираем столбец, в котором нарушено условие неотрицательности (для задачи на максимум) или отрицательности (для задачи на минимум). Если таких столбцов несколько, разрешающий будет тот, которому соответствует наибольшее по модулю значение элемента заключительной строки, т.е. .

За ведущий выберем столбец 3 , так как -3 наименьший элемент в L строке. Элемент L строки, принадлежащий столбцу свободных членов не рассматриваем.

базисные переменные	x1	x2	x3	свободные члены
y1	2	- 1	1	3
y2	- 4	2	- 1	6
y3	3	0	1	15
G	1	- 1	- 3	0