
диОСК
.pdfВведем весьма существенное для теории краевого эффекта допущение, вытекающее из быстрой изменяемости решения по переменной s. Из выражения
w = w0 + wK = w0 +e−kα (C1 cos kα +C2 sin kα)
следует, что для цилиндрической оболочки составляющая wK пропорциональна e-kα, т. е. при дифференцировании по α она умножается на -k. Если k велико, то можно утверждать, что функции, описывающие краевой эффект, при дифференцировании существенно возрастают по абсолютной величине, т. е. в уравнениях краевого эффекта можно пренебречь низшими производными по сравнению с высшими. Из этого, в частности, следуёт, что согласно полученным зависимостямκαK >>κβK
и общие соотношения между моментами и изменениями кривизн
Mα = D (κα + µ κβ ), M β = D (κβ + µ κα )
можно приближенно записать с учетом полученных выше зависимостей в виде
MαK = D καK = −D |
d 2 wK |
, |
M βK = µ MαK = D µ καK = −D µ |
d 2 wK |
|
ds2 |
ds2 |
||||
|
|
|
Выведем теперь уравнение краевого эффекта. В соответствии с принятыми выше допущениями(NαK << NβK ) в первом уравнении равновесия пренебрегаем членами,
содержащимиQαK иNαK при этом считаем, что у непологой оболочки ctgψ не является большой величиной, а радиус R1 не является малым по сравнению с радиусом R2.

ВО втором уравнении равновесия |
|
|
dMαK |
|
|
K |
K |
) |
ctgψ |
|
|
|
|
K |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
(Mα |
−M β |
R |
−Qα |
|
= 0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ds |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
пренебрегаем вторым членом, содержащим |
|
MαK иM |
βK = µ MαK по сравнению с |
|||||||||||||||||||||||||||||||||||
первым членом, представляющим производную от быстроизменяющейся функции. |
||||||||||||||||||||||||||||||||||||||
Тогда с учетом полученных выражений для моментов из второго уравнения |
||||||||||||||||||||||||||||||||||||||
равновесия будем иметь |
|
|
|
|
dM K |
|
|
|
|
|
d 3wK |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
QK = |
|
|
= −D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
α |
|
|
|
ds |
|
|
|
|
|
|
ds3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
NβK |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dQK |
|
|
|
|
ctgψ |
|
|
N K |
|
|
|
||||||||||||
а из первого уравнения равновесия |
|
|
|
|
α |
|
+QαK |
|
|
− |
|
α |
|
− |
|
|
|
|
|
= 0 |
||||||||||||||||||
|
|
|
ds |
|
R |
|
|
R |
|
|
R |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
2 |
|
|
||
с учетом указанных выше допущений получим |
d 4 wK |
|
|
NβK |
|
|
|
|
||||||||||||||||||||||||||||||
D |
ds4 |
+ |
|
|
|
|
= 0 |
|
||||||||||||||||||||||||||||||
|
|
R |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||
Запишем выражения для окружной деформации εK |
. Из равенств |
|||||||||||||||||||||||||||||||||||||
εβ = 1 (u cosα + w sin α) |
и εβ = |
|
|
|
1 |
|
(Nβ −µ Nαβ) с учетом принятых |
|||||||||||||||||||||||||||||||
|
|
E h |
||||||||||||||||||||||||||||||||||||
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
допущений и формулыR2 = r sin α |
|
|
|
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
NβK |
|||||||||||||||||
К |
1 |
|
K |
|
|
K |
|
w |
|
К |
|
|
|
1 |
|
|
|
K |
|
|
|
|
|
K |
|
|
|
|
||||||||||
εβ = |
|
(u |
|
ctgα |
+ w |
|
|
|
)≈ |
|
|
|
K , |
εβ |
= |
|
|
|
|
(Nβ |
−µ Nα |
)≈ |
|
|
|
|
||||||||||||
R |
|
|
|
|
|
|
|
E h |
|
E h |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
|
|
|
|
E h |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Приравнивая получим NβK ≈ |
|
|
wK |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Подставляя полученное выражение в |
D |
d 4 wK |
+ |
NβK |
= 0 |
||||||||
ds4 |
R |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
d 4 wK |
|
|
|
|
|
|
|
|
|
2 |
|
|
получим |
+4 k |
4 |
w |
K |
= 0 где |
k 4 |
= E h (4 D R22 )= 3 (1−µ2 ) (R22 h2 ) |
||||||
ds4 |
|
|
|||||||||||
Здесь радиус R2 в пределах зоны краевого эффекта можно считать постоянным и равным его значению на рассматриваемом крае. Отметим, что полученное линейное ДУ аналогично однородному уравнению, соответствующему уравнению для цилиндрической оболочки. Затухающая часть решения аналогична выражению для затухающей части цилиндрической оболочки, т. е.
wK = e−k s (C1 cos ks +C2 sin ks)
Используя дифференциальные зависимости находим
ϑК = − dwK |
= −k e−k s [C |
(cos ks +sin ks)−C |
2 |
(cos ks −sin ks)], |
|||||
ds |
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
M K = −D |
d 2 wK |
= −2 D k 2 e−k s (C |
sin ks −C |
2 |
cos ks), |
||||
|
|||||||||
α |
ds2 |
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
QαK = −D d 3w3K ds
M βK = µ MαK ,
= −2 D k3 e−k s [C |
(cos ks −sin ks)+C |
2 |
(cos ks +sin ks)] |
|||
|
1 |
|
|
|
|
|
N K = ctgψ |
QK , N K = |
E h |
wK . |
|
|
|
|
|
|
||||
α |
α |
β |
R2 |
|
|
|
|
|
|
|
|
|
|

На крае оболочки усилия NαK и QαK приводятся к радиальной силе ТK см. верхний рисунок
T K = −(NαK cosψ +QαK sinψ )= −QαK 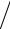 sinψ
sinψ
Радиальное перемещение за счет краевого изгиба определяется приближенной формулой, следующей из ur = u cosα + w sin α
urK ≈ wK sinψ
Положительные направления кинематических и силовых факторов на краях оболочки показаны на нижнем рисунке.
Произвольные постоянные С1 и С2, входящие в полученные равенства удобно
выразить через радиальное перемещение и угол поворота на крае оболочки s=0.
Полагая в (4.86)... (4.89) s — 0, ψ “ ф, получим
