J

Уровень запаса

k – число партий

b

b

b

b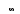

t

0

4T

Время

Т0

2Т

3Т

4Т

T₁

T₂

T₁

T₁

T₁

T₂

T₂

Т₁

Т₂

T₂



Рис. 4.

Необходимость покрытия дефицита приводит к тому, что максимальный уровень запаса s в момент поступления каждой партии теперь не равен её объёму n, а меньше его на величину дефицита n-s, накопившегося за время Т₂ (см. рис. 4).

Из геометрических соображения легко установить, что

(17)

В данной модели в функцию суммарных затрат С наряду с затратами С₁ (на пополнение запаса) и С₂ (на хранение запаса) необходимо ввести затраты С₃ – на штраф из-за дефицита, т.е.

С=С₁+С₂+С₃

Затраты С₁, как и ранее находим по формуле (11). В разд. 2.2 было показано, что затраты С₂ при линей ном расходе запаса равны затратам на хранение среднего запаса, который за время потребления Т₁ равен sT₁/2; поэтому с учётом (7) и (5) эти затраты составят

(18)

При расчёте затрат С₃ будем считать, что штраф за дефицит составляет в единицу времени с₃ на каждую единицу продукта. Так как средний уровень дефицита за период Т₂ равен (n-s), то штраф за этот период Т₂ составит , а за весь период  с учётом (7) и (19) –

(19)

Теперь учитывая (12), (18) и (19) суммарные затраты равны

(20)

Нетрудно заметить, что при n=s формула (19) совпадает с ранее полученной (8) в модели без дефицита.

Рассматриваемая задача управления запасами сводится к отысканию такого объёма партии и максимального уровня запаса , при которых функция С (19) принимает минимальное значение. Другими словами, необходимо исследовать функцию двух переменных С(n,s) на экстремум. Приравнивая частные производные к нулю, получим после преобразования систему уравнений:

(21)

Решая систему, получаем формулы наиболее экономичного объёма партии и максимального уровня запасадля модели с дефицитом¹:

,(22)

.(23)

Величина

(24)

называется плотностью убытков из-за неудовлетворительного спроса и играет важную роль в управлении запасами. Заметим, что 0    1. Если значение с₃ мало по сравнению с с_2, то величина  близка к нулю: когда с₃ значительно превосходит с₂, то  близка к 1. Недопустимость дефицита равносильна предположению, что с₃   или  = 1.

Используя (24) основные формулы (22) и (23) можно записать компактнее:

, (25)

(26)

Следует учесть, что в силу (17) и (26) и . Поэтому утверждение о том, что плотность убытков из-за неудовлетворительного спроса равна , означает, что в течение (1–)100% времени от полного периода Т запас продукта будет отсутствовать.

Из сравнения (25) и (10) следует, что оптимальные объёмы партий для задач с дефицитом и без дефицита при одинаковых параметрах связаны соотношением:

(27)

откуда вытекает, что оптимальный объём партии в задаче с дефицитом всегда больше (в1/ ), чем для задач без дефицита.

Задача 4. Найти наиболее экономичный объём партии и интервал между поставками, сохраняя условия задачи 2, кроме недопустимости дефицита, если известно, что отсутствие на сборке каждой детали приносит в сутки убытки в размере 3,5 ден. ед.

Решение. По условию с₃=3,5. Ранее при решении задачи 2 было получено по формуле (9) =4335 и по (15) Т₀=13,2. Найдём плотность убытков из-за неудовлетворённого спроса по формуле (24): =3,5/(0,35+3,5)=0,909, т.е. 100(1– 0,909)=9,1% времени между поставками детали на сборке будут отсутствовать.

Теперь оптимальный размер партии по формуле (27) . В силу (15) пропорционально увеличениюдолжен увеличиться интервал между поставками, т.е.

.