
- •Федеральное агенство морского и речного транспорта
- •Оценка точности места судна методом эллипса погрешностей.
- •Упрощенный способ построения эллипса погрешности.
- •Расчет элементов эллипса погрешностей с помощью приложения 5 мт-75.
- •Расчет элементов эллипса погрешностей с помощью таблицы 4.11 мт-2000. (Оценка точности места судна по двум линиям положения).
- •Оценка точности определения места судна с помощью средней квадратической погрешности обсервованной точки. Расчетные формулы скп обсервованной точки.
- •Упрощенные формулы для вычисления скп обсервованной точки.
- •Влияние на точность обсервации систематических погрешностей измерений навигационных параметров. Оценка смещения места судна под действием систематических погрешностей измерений.
Оценка точности определения места судна с помощью средней квадратической погрешности обсервованной точки. Расчетные формулы скп обсервованной точки.
В качестве точечной
– выражаемой одним числом – оценки
положения точки на плоскости в геодезии,
гидрографии и навигации широко применяют
среднюю квадратическую погрешность
точки. СКП обсервованного места судна
обозначают буквой
![]() и часто называютрадиальной
погрешностью.
Такое название связано с тем, что
геометрически СКП
и часто называютрадиальной
погрешностью.
Такое название связано с тем, что
геометрически СКП
![]() представляется радиусом окружности с
центром в обсервованной точке. Иначе
величину
представляется радиусом окружности с
центром в обсервованной точке. Иначе
величину![]() можно трактовать как диагональ
прямоугольника, построенного на полуосях
эллипса погрешностей:
можно трактовать как диагональ
прямоугольника, построенного на полуосях
эллипса погрешностей:
![]() (9)
(9)
Данная формула
показывает связь СКП
![]() обсервованной точки с элементами эллипса
погрешностей рисунок (3).
обсервованной точки с элементами эллипса
погрешностей рисунок (3).
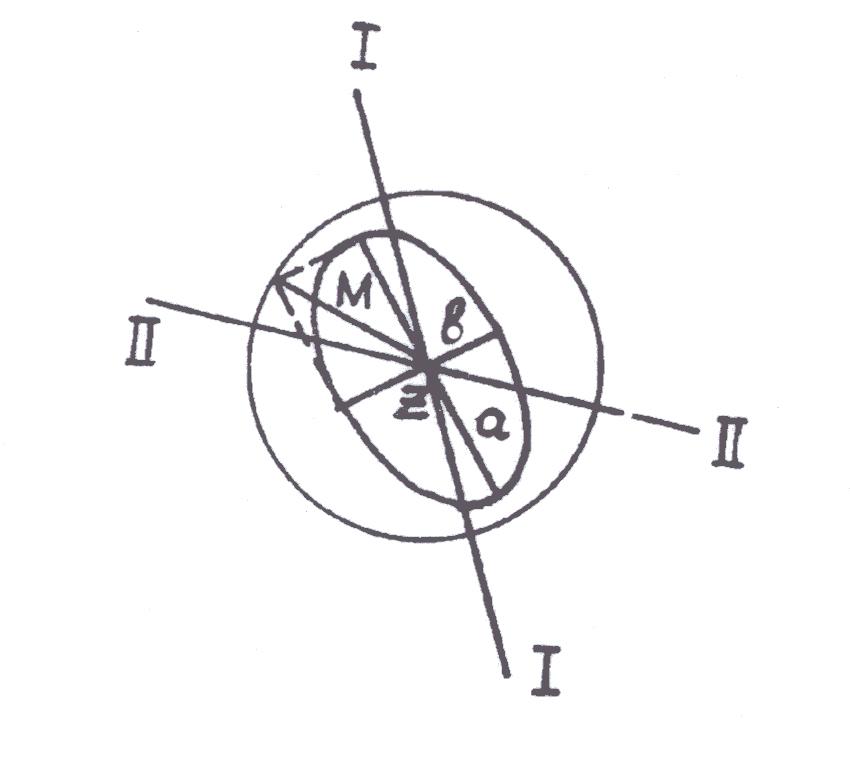
Рис. 5
![]() Оценка
точности места судна с помощью СКП
Оценка
точности места судна с помощью СКП
![]() является менее строгой в теоретическом
отношении по сравнению с методом эллипса
погрешностей. Но расчет и построение
СКП
является менее строгой в теоретическом
отношении по сравнению с методом эллипса
погрешностей. Но расчет и построение
СКП![]() очень просты, что и предопределяет ее
более частое применение.
очень просты, что и предопределяет ее
более частое применение.
Вычисление СКП
![]() по известным или задаваемым средним
квадратическим погрешностям
по известным или задаваемым средним
квадратическим погрешностям![]() и
и![]() измерений навигационных параметров
производится по формуле:
измерений навигационных параметров
производится по формуле:
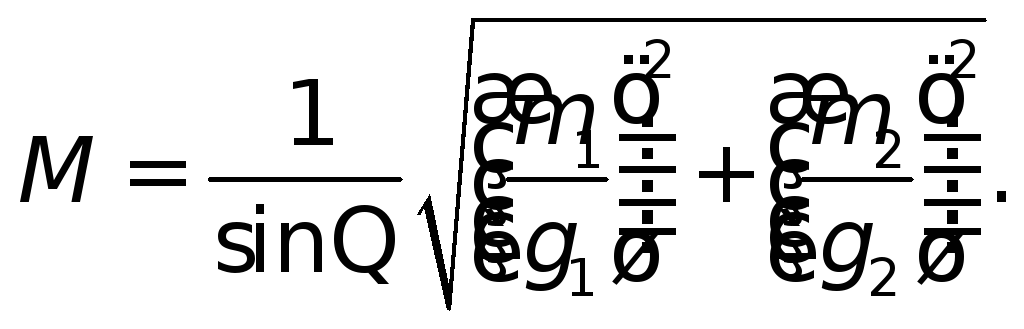 (10)
(10)
Здесь
![]() и
и![]() - модули градиентов навигационных
параметров;
- модули градиентов навигационных
параметров;
![]() - угол между линиями
положения.
- угол между линиями
положения.
Из формулы (10)
следует, что погрешность
![]() места судна будет тем меньше, чем меньше
СКП
места судна будет тем меньше, чем меньше
СКП![]() и
и![]() измерений параметров и чем больше
градиенты этих параметров. Кроме того,
СКП
измерений параметров и чем больше
градиенты этих параметров. Кроме того,
СКП![]() зависит от угла
зависит от угла![]() ,
стремясь к минимуму при
,
стремясь к минимуму при![]() .
.
Величину
![]() можно также выразить через смещения
можно также выразить через смещения![]() и
и![]() линий положения:
линий положения:
![]() (11)
(11)
![]() СКП
СКП
![]() обсервованной точки выражается в милях
или кабельтовых. Вероятность того,
действительное место судна находится
в области, ограниченной окружностью
радиуса
обсервованной точки выражается в милях
или кабельтовых. Вероятность того,
действительное место судна находится
в области, ограниченной окружностью
радиуса![]() составляет
составляет![]() Значение вероятности
Значение вероятности![]() зависит от соотношений полуосей эллипса
погрешностей:
зависит от соотношений полуосей эллипса
погрешностей:
при
![]()
![]() или
или![]()
при
![]()
![]()
![]() или
или![]()
Вероятность
удвоенной СКП
![]() составляет
составляет![]() Поэтому величина
Поэтому величина![]() часто применяется в практических задачах
в качестве предельной погрешности
обсервованной точки.
часто применяется в практических задачах
в качестве предельной погрешности
обсервованной точки.
Проекция
![]() радиальной погрешности
радиальной погрешности![]() на
два взаимно перпендикулярных направления,
например, на меридиан и параллель,
принимаются:
на
два взаимно перпендикулярных направления,
например, на меридиан и параллель,
принимаются:
![]()
Вероятность
нахождения места судна в области,
ограниченной окружностью радиуса
![]() ,
можно определить с помощью табл. 1-в
МТ-75 или табл. 4.13 МТ-2000.
,
можно определить с помощью табл. 1-в
МТ-75 или табл. 4.13 МТ-2000.
Аргументами для
входа в таблицу служат отношение полуосей
эллипса погрешностей
![]() и отношение
и отношение![]() показывающее, во сколько раз заданная
погрешность
показывающее, во сколько раз заданная
погрешность![]() больше СКП
больше СКП![]() обсервованной точки. Отношение
обсервованной точки. Отношение![]() называют также нормированной СКП. Его
можно понимать как соотношение заданного
радиуса
называют также нормированной СКП. Его
можно понимать как соотношение заданного
радиуса![]() окружности, в пределах которой с
определенной вероятностью находится
место судна, и радиуса
окружности, в пределах которой с
определенной вероятностью находится
место судна, и радиуса![]() окружности, которая соответствует СКП
места судна с вероятностью
окружности, которая соответствует СКП
места судна с вероятностью![]() С помощью табл.1-в МТ-75 и табл. 4.13 МТ-2000
можно решать задачи двух видов.
С помощью табл.1-в МТ-75 и табл. 4.13 МТ-2000
можно решать задачи двух видов.
Пример. Место
судна определено со средней квадратической
погрешностью
![]() .
Какова вероятность того, что судно
находясь в границах окружности с радиусом
.
Какова вероятность того, что судно
находясь в границах окружности с радиусом![]()
Решение. Вначале
вычисляем
![]() по аргументам
по аргументам![]() и
и![]()
![]() с помощью табл. 1-в МТ-75 или табл. 4.13
МТ-2000 определили
с помощью табл. 1-в МТ-75 или табл. 4.13
МТ-2000 определили![]()
Пример.
Судно входит в узкость шириной 6 миль.
Приняли
![]() С какой точностью необходимо определять
место судна, чтобы находиться на своей
стороне движения с вероятностью
С какой точностью необходимо определять
место судна, чтобы находиться на своей
стороне движения с вероятностью![]()
Решение. По
аргументам
![]() и
и
![]() из табл. 1-в МТ-75 или табл. 4.13 МТ-2000 выбрали
из табл. 1-в МТ-75 или табл. 4.13 МТ-2000 выбрали![]() Затем вычислили искомую величину СКП:
Затем вычислили искомую величину СКП:
![]() т.е.
т.е.
![]()
