- •Федеральное агенство морского и речного транспорта
- •Оценка точности места судна методом эллипса погрешностей.
- •Упрощенный способ построения эллипса погрешности.
- •Расчет элементов эллипса погрешностей с помощью приложения 5 мт-75.
- •Расчет элементов эллипса погрешностей с помощью таблицы 4.11 мт-2000. (Оценка точности места судна по двум линиям положения).
- •Оценка точности определения места судна с помощью средней квадратической погрешности обсервованной точки. Расчетные формулы скп обсервованной точки.
- •Упрощенные формулы для вычисления скп обсервованной точки.
- •Влияние на точность обсервации систематических погрешностей измерений навигационных параметров. Оценка смещения места судна под действием систематических погрешностей измерений.
Упрощенный способ построения эллипса погрешности.
Упрощенный способ
построения эллипса заключается в том,
что по формуле![]() вычисляются смещения
вычисляются смещения![]() и
и![]() линий положения и откладываются по
нормалям к соответствующим линиям
положения. Через концы отрезков
линий положения и откладываются по
нормалям к соответствующим линиям
положения. Через концы отрезков![]() и
и![]() проводятся прямые, параллельные линиям
положения, которые образуют фигуру
погрешности в виде параллелограмма
(ромба, прямоугольника, квадрата).
проводятся прямые, параллельные линиям
положения, которые образуют фигуру
погрешности в виде параллелограмма
(ромба, прямоугольника, квадрата).
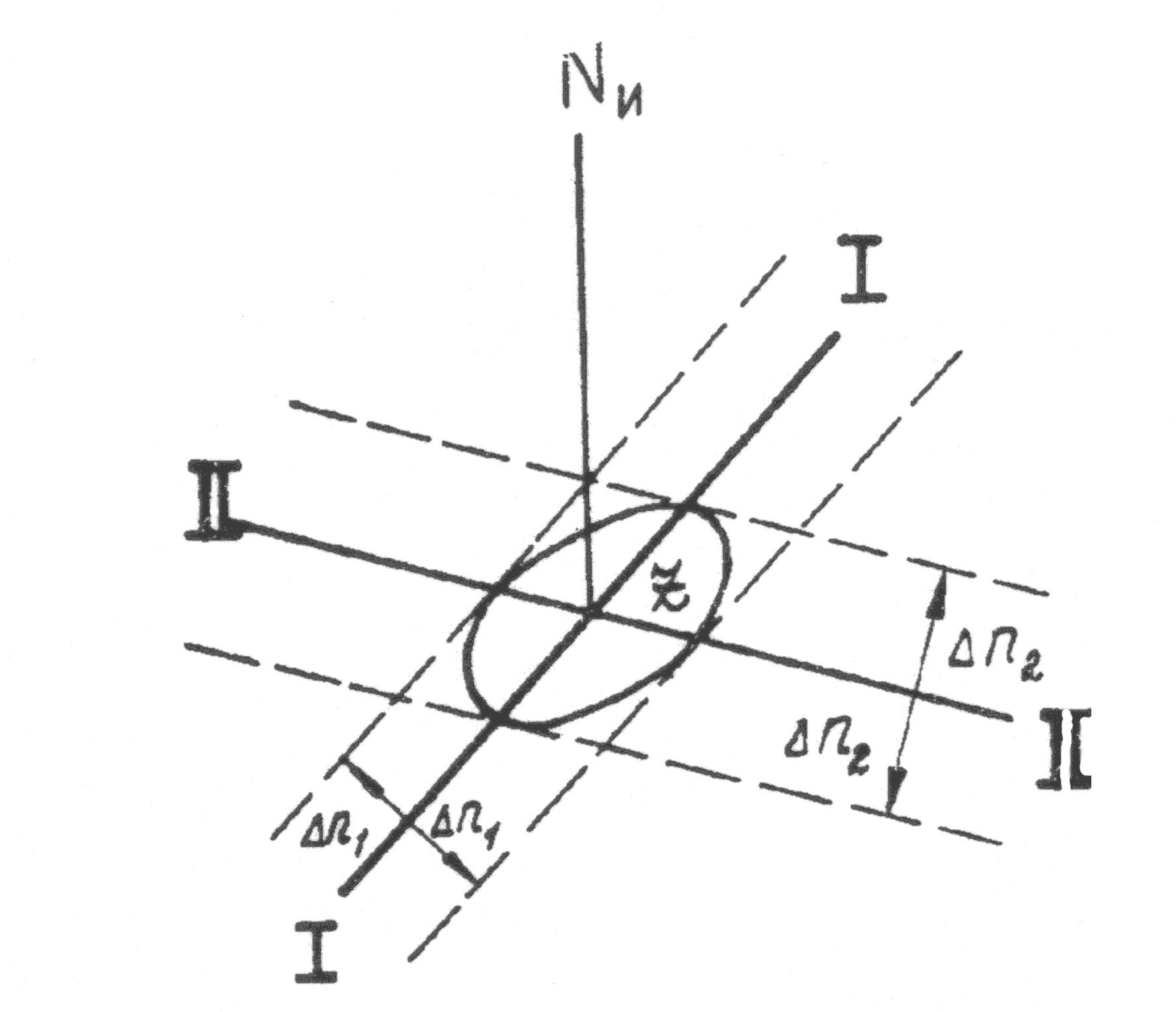
Рис. 2
В фигуру погрешности от руки вписывается эллипс, точнее – овал. Он обязательно должен проходить через четыре точки, в которых пересекаются основные и смещенные линии положения.
Пример.
По пеленгам двух
радиомаяков определили место судна.
Сделать упрощенное построение эллипса
погрешностей, если
![]() ,
с карты сняли
,
с карты сняли![]()
![]() ,
с карты сняли
,
с карты сняли![]()
![]() ,
,![]()
Решение. 1. Приняли модули градиентов радиомаяков
![]()
![]()
2. Вычисляем смещения линий положения:
![]()
![]()
3. На карте в
обсервованной точке построили
перпендикуляр к линии первого пеленга
и отложили на нем в противоположных
направлениях отрезки
![]() ;
через их концы построили смещенные
линии положения
;
через их концы построили смещенные
линии положения![]() и
и![]() .
Затем по нормали к линии второго пеленга,
т.е. ко второй линии положения, отложили
отрезки
.
Затем по нормали к линии второго пеленга,
т.е. ко второй линии положения, отложили
отрезки![]() и, через их концы, построили смещенные
линии положения
и, через их концы, построили смещенные
линии положения![]() и
и![]() ,
параллельные второй линии положения.
В образовавшийся параллелограмм вписали
овал.
,
параллельные второй линии положения.
В образовавшийся параллелограмм вписали
овал.
Расчет элементов эллипса погрешностей с помощью приложения 5 мт-75.
В приложении 5 МТ-75 дана таблица для расчета элементов эллипса погрешностей при определении места судна по двум линиям положения.
Элементы эллипса рассчитываются по формулам:
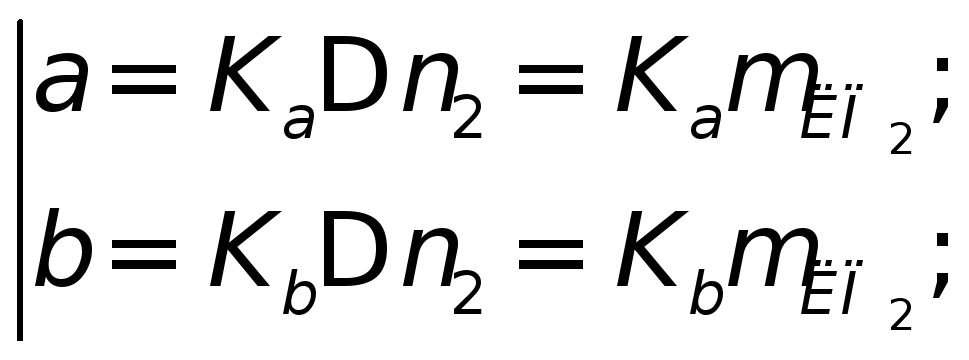 (8)
(8)
![]() ,
,
где
![]() -
среднее квадратическое смещение более
точной линии положения; в приложении 5
оно обозначено
-
среднее квадратическое смещение более
точной линии положения; в приложении 5
оно обозначено![]()
Величины
![]() выбираются из таблицы приложения 5.
Входными аргументами в таблицу являются:
выбираются из таблицы приложения 5.
Входными аргументами в таблицу являются: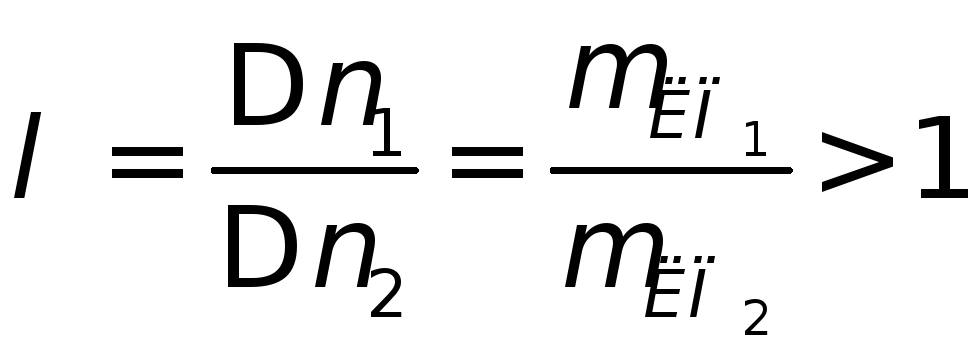 и острый угол
и острый угол![]() между линиями положения. При этом индекс
2 приписывается более точной линии
положения.
между линиями положения. При этом индекс
2 приписывается более точной линии
положения.
Направление![]() большой
полуоси
большой
полуоси![]() определяют по углу
определяют по углу![]() ,
который откладывают внутри острого
угла
,
который откладывают внутри острого
угла![]() от направления более точной линии
положения
от направления более точной линии
положения![]() .
.
Пример.
Место судна
определено по двум радиолокационным
расстояниям. Определить элементы эллипса
погрешностей по приложению 5 МТ-75, если
![]()
![]()
![]()
Решение.
1. Градиент
расстояний
![]()
2. Рассчитали переносы:
![]()
![]()
Более точной является первая линия положения, поэтому приписали ей индекс 2 и рассчитали:
![]()
3. По
![]() и по
и по![]() выбрали из приложения
выбрали из приложения![]()
![]()
![]() .
.
При выборке из таблицы приложения 5 необходимо производить интерполяцию.
4. Рассчитали элементы эллипса погрешностей по формулам (8):
![]()
![]()
Пример.
Место судна
определено по пеленгу ориентира
![]() и радиолокационному расстоянию до
ориентира
и радиолокационному расстоянию до
ориентира![]() Рассчитать элементы эллипса погрешностей
пользуясь приложением 5 МТ-75, если
Рассчитать элементы эллипса погрешностей
пользуясь приложением 5 МТ-75, если![]() с карты определили
с карты определили![]()
![]() 4
с карты определили
4
с карты определили![]()
![]()
![]()
Решение.
1.
![]()
![]()
Вторая линия положения – более точная.
2.
![]()
3. По
![]() и
и![]() выбрали из приложения 5 МТ-75
выбрали из приложения 5 МТ-75![]()
![]()
![]()
4. рассчитали элементы эллипса погрешностей:
![]()
Так как направление
![]() составляет
составляет![]() то направление большой оси эллипса
то направление большой оси эллипса![]()
Расчет элементов эллипса погрешностей с помощью таблицы 4.11 мт-2000. (Оценка точности места судна по двум линиям положения).
В таблице даны
коэффициенты
![]() ,
,![]() и угол
и угол![]() для определения элементов среднего
квадратического эллипса погрешностей
(СКЭ, ЭСКП), а также коэффициент
для определения элементов среднего
квадратического эллипса погрешностей
(СКЭ, ЭСКП), а также коэффициент![]() для расчета радиальной средней
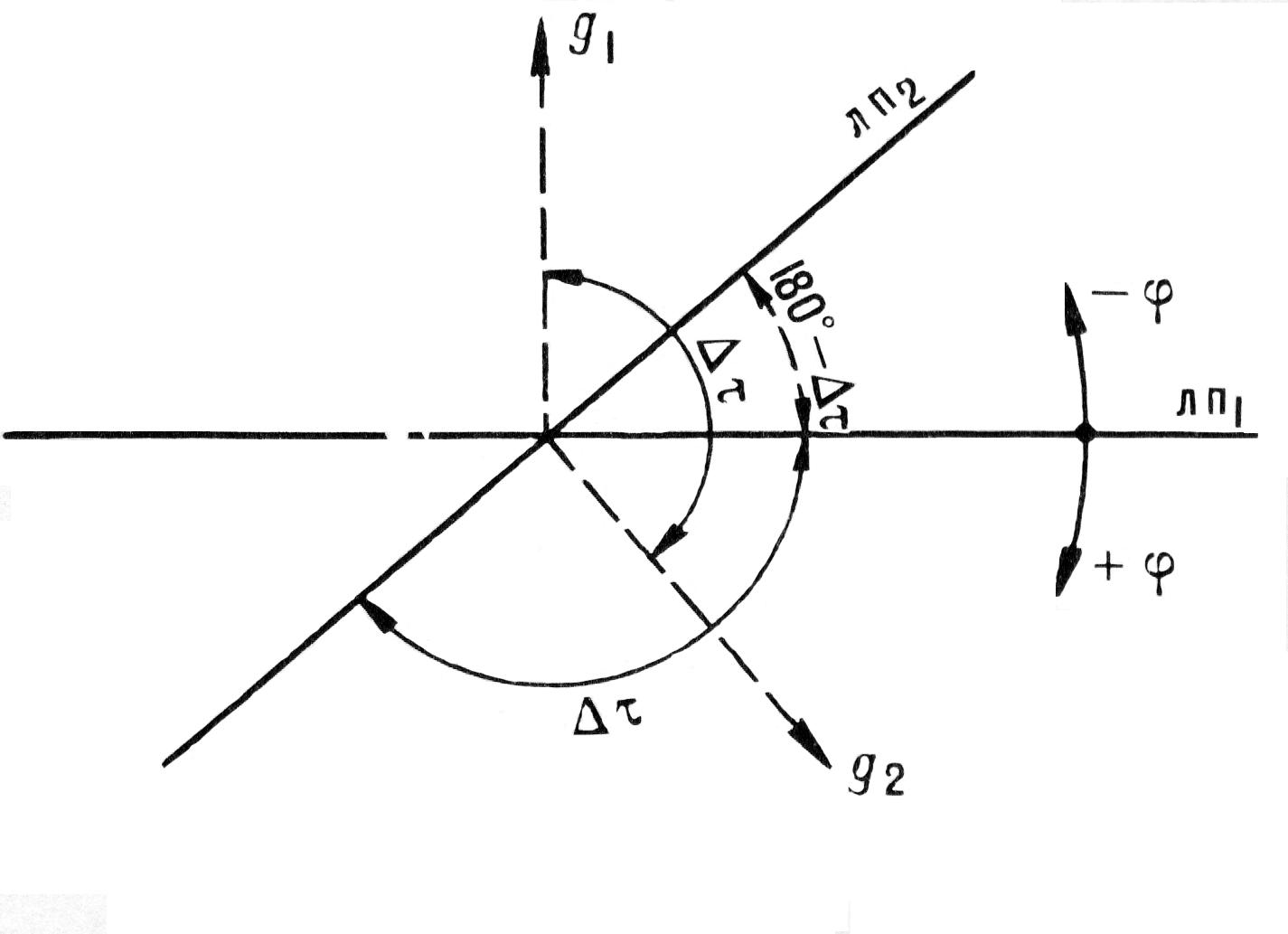
квадратической погрешности (РСКП) места
по двум линиям положения (Рис.3, Рис.4)
для расчета радиальной средней
квадратической погрешности (РСКП) места
по двум линиям положения (Рис.3, Рис.4)
Аргументами для входа в таблицу являются:
- априорное значение
коэффициента взаимной корреляции
![]() линии положения (навигационных параметров)
в пределах
линии положения (навигационных параметров)
в пределах![]() с интервалом
с интервалом![]() ;
при независимых линиях положения или
при отсутствии данных об их корреляции
в таблицу входят с
;
при независимых линиях положения или
при отсутствии данных об их корреляции
в таблицу входят с![]()
- коэффициент
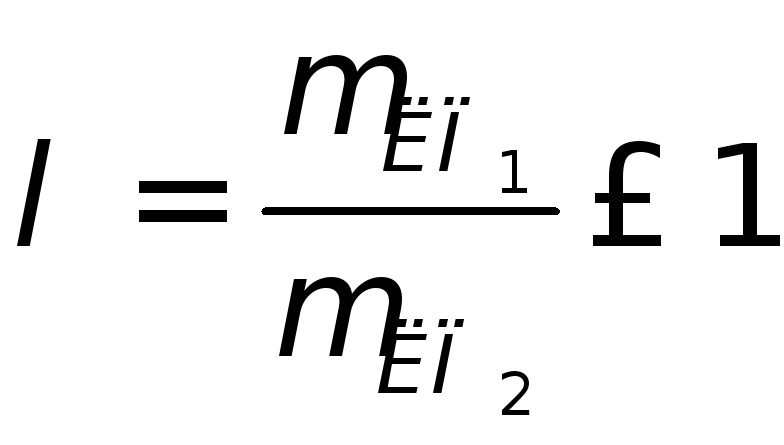 в пределах
в пределах![]() с интервалом
с интервалом![]() где
где![]() -
полная СКП более точной линии положения,
а
-
полная СКП более точной линии положения,
а![]() -
полная СКП менее точной линии положения
-
полная СКП менее точной линии положения![]()
- угол
![]() между направлениями градиентов линий
положения в пределах от 20 до 1600
с интервалом 100
.
между направлениями градиентов линий
положения в пределах от 20 до 1600
с интервалом 100
.
Коэффициенты
![]() и
и![]() служат для расчета полуосей среднего
квадратического эллипса погрешностей:
служат для расчета полуосей среднего
квадратического эллипса погрешностей:![]()
|
Рис.3 |
Рис.4 |
Направление большой
оси эллипса погрешностей фиксирует
угол
![]() ,
который всегда откладывается от более
точной линии положения. Модуль
положительного угла
,
который всегда откладывается от более
точной линии положения. Модуль
положительного угла![]() откладывается
внутрь угла между линиями положения,
равного
откладывается
внутрь угла между линиями положения,
равного![]() .
Модуль отрицательного угла
.
Модуль отрицательного угла![]() откладывается
внутрь угла между линиями положения,
равного
откладывается
внутрь угла между линиями положения,
равного![]() Если
Если![]() и
и![]() то за угол
то за угол![]() между линиями положения принимается
тот, который образован направлениями
между линиями положения принимается
тот, который образован направлениями![]() и
и![]() или направлениями
или направлениями![]() и
и![]() .
.
Коэффициент
![]() служит для расчета РСКП места:
служит для расчета РСКП места:
![]()
Таблица рассчитана по формулам:
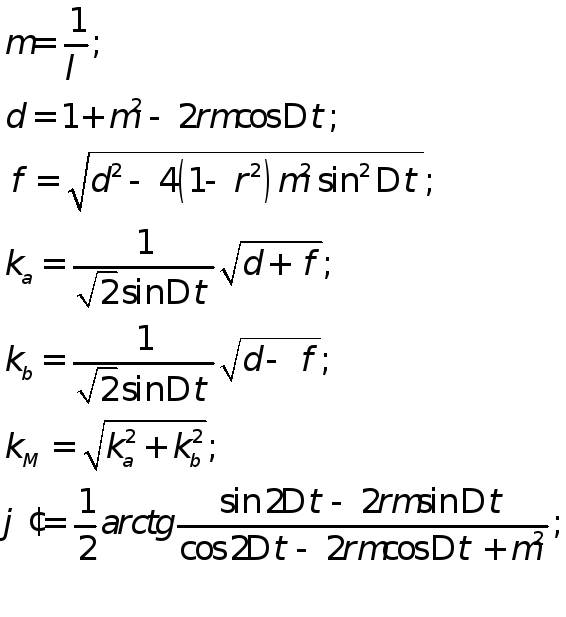
![]()
![]()
![]()
![]() и
и
![]()
![]()
![]() и
и
![]()
Полуоси эллипса
погрешностей
![]() соответствующего заданной вероятности
соответствующего заданной вероятности![]() рассчитываются по формулам:
рассчитываются по формулам:
![]()
![]()
где
![]() -
коэффициент, выбираемый из табл. 4.12
МТ-2000 по заданной вероятности
-
коэффициент, выбираемый из табл. 4.12
МТ-2000 по заданной вероятности![]() .
.
Радиальная
погрешность
![]() заданной вероятности
заданной вероятности![]() вычисляется по формуле
вычисляется по формуле
![]()
где
![]() -
коэффициент, выбираемый из табл. 4.14
МТ-2000 по заданной вероятности
-
коэффициент, выбираемый из табл. 4.14
МТ-2000 по заданной вероятности![]() и отношению полуосей эллипса погрешностей
и отношению полуосей эллипса погрешностей![]()
Пример.
Место судна получено
по двум взаимонезависимым линиям
положения
![]() .
Направления градиентов линий положения
.
Направления градиентов линий положения![]() и
и![]() СКП линий положения
СКП линий положения![]() и
и![]() Определить эллиптическую и радиальную
средние квадратические погрешности
места.
Определить эллиптическую и радиальную
средние квадратические погрешности
места.
Решение.
По
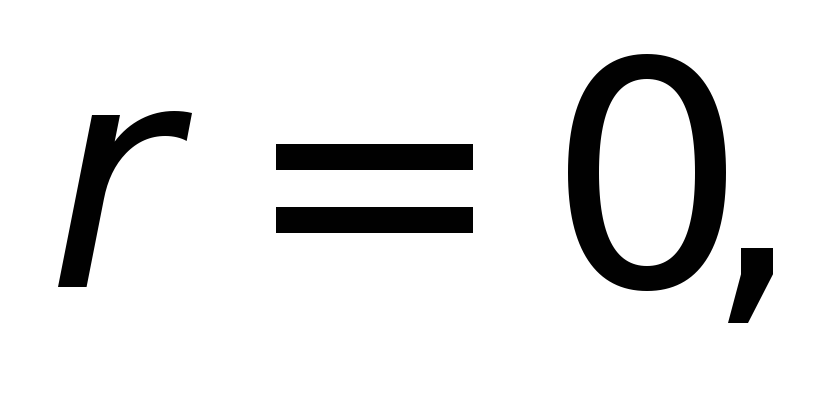
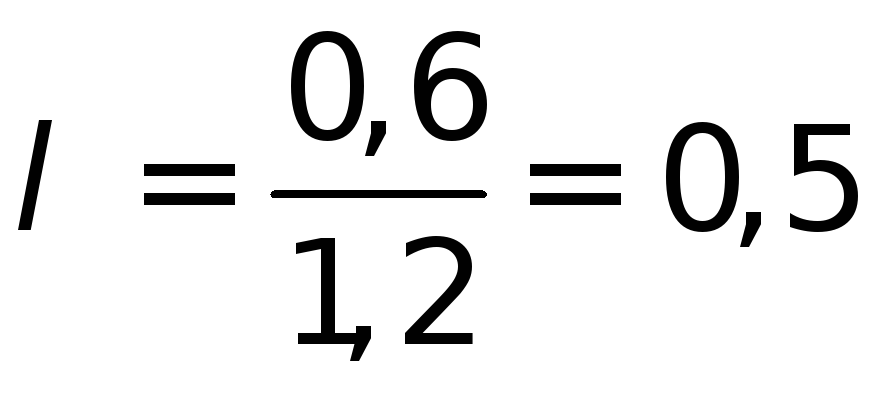 и
и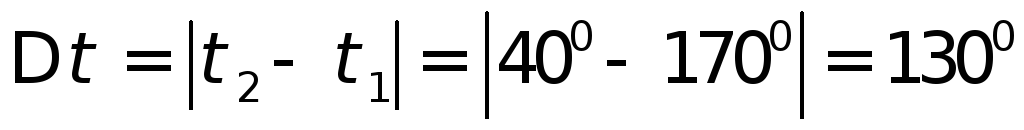 из табл.4.11а выбираем
из табл.4.11а выбираем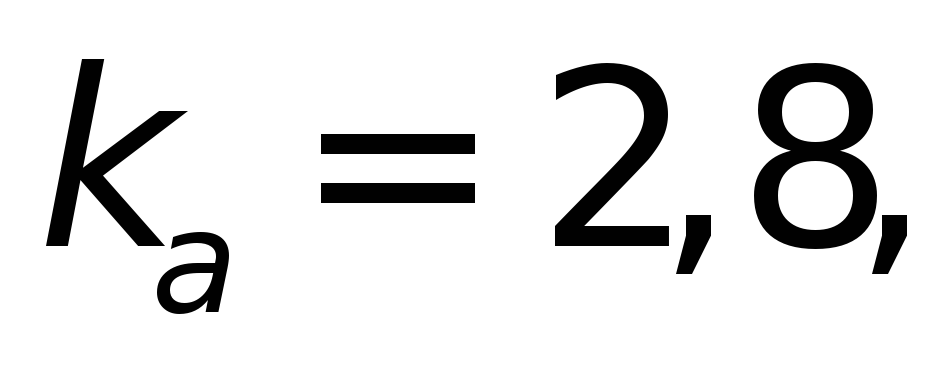
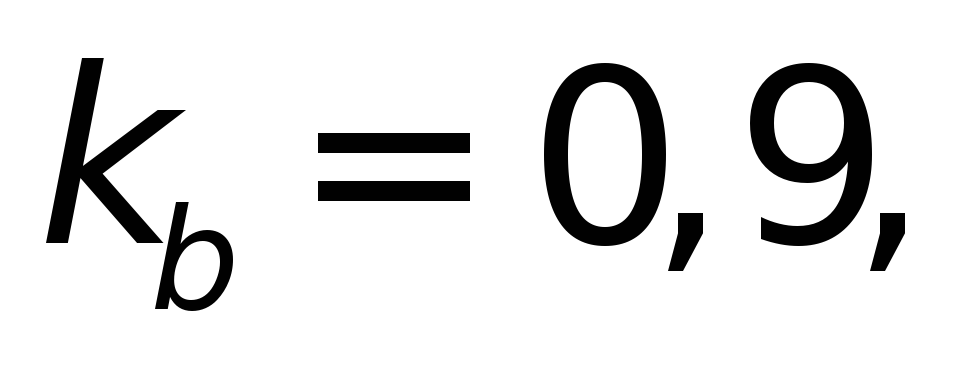
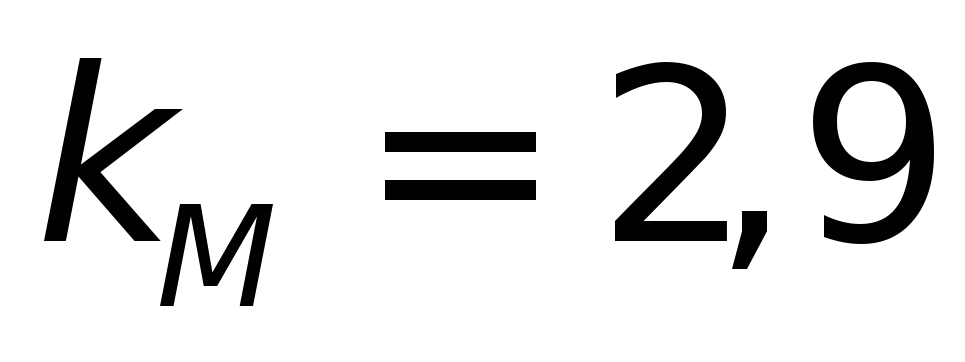 и
и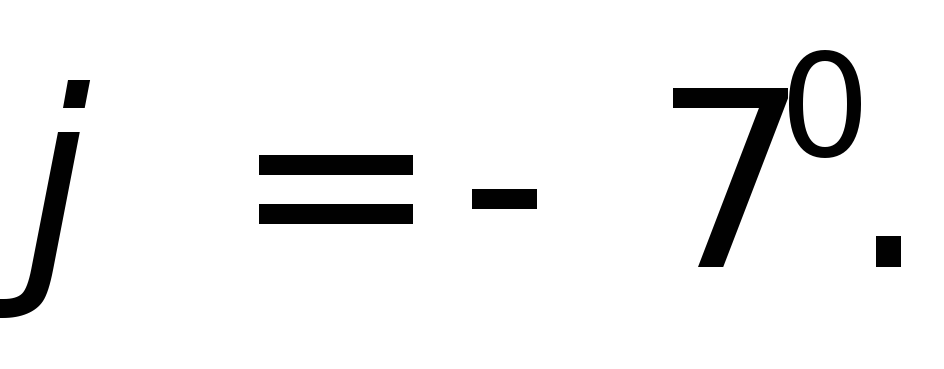
Вычисляем элементы среднего квадратического эллипса погрешностей:
![]()
![]()
От более точной линии положения внутрь угла между линиями положения
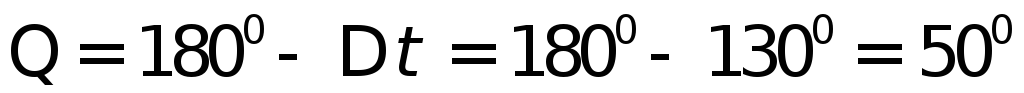 (т.к. угол
(т.к. угол отрицательный) откладываем угол
отрицательный) откладываем угол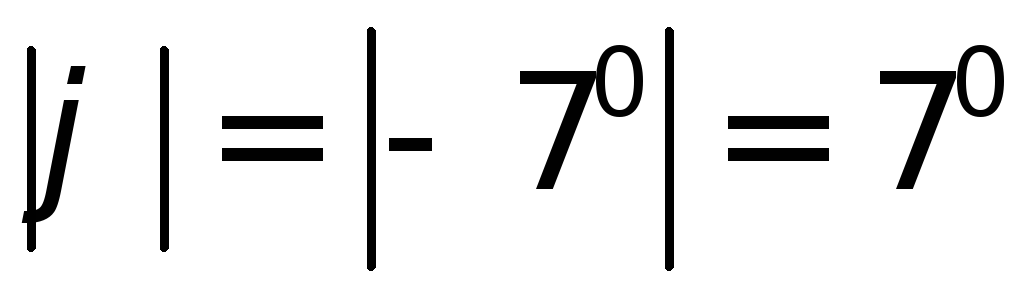 и, тем самым, определяем направление
большой оси эллипса погрешностей.
и, тем самым, определяем направление
большой оси эллипса погрешностей.Вычисляем радиальную СКП места:
![]()
Этот же результат получим по формуле:
![]()
Пример.
Полные СКП линий
положения
![]() и
и![]() Коэффициент взаимной корреляции
Коэффициент взаимной корреляции![]() Направления градиентов линий положения
Направления градиентов линий положения![]() и
и![]() Определить эллиптическую и радиальную
средние квадратические погрешности
места.
Определить эллиптическую и радиальную
средние квадратические погрешности
места.
Решение.
По
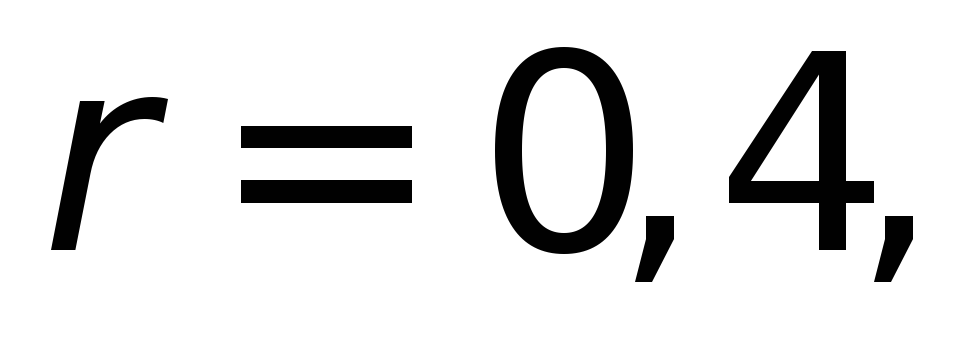
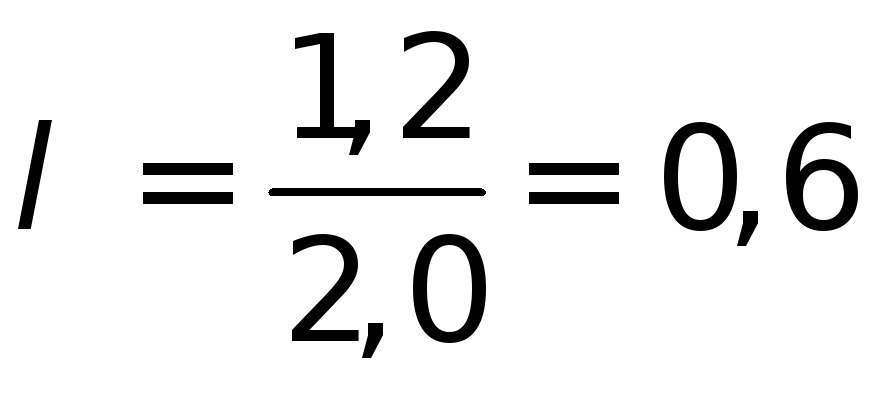 и
и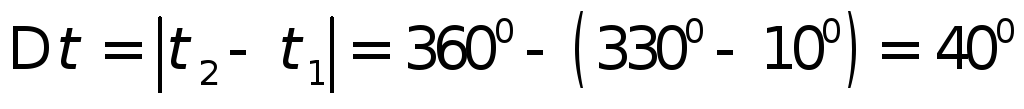 из табл.4.11в выбираем
из табл.4.11в выбираем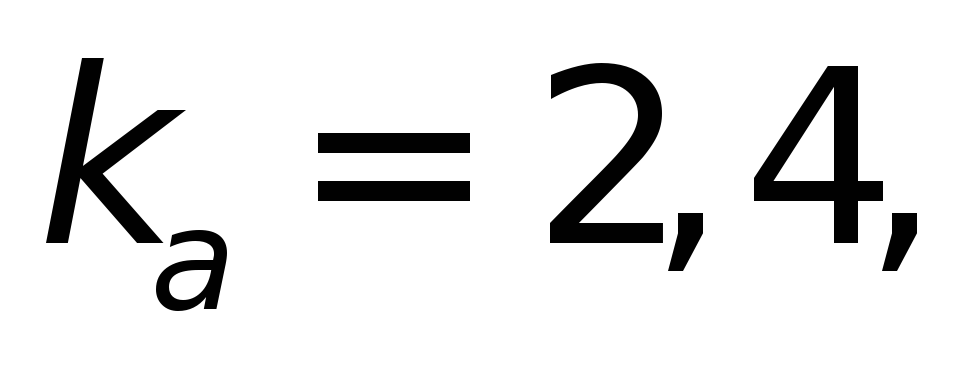
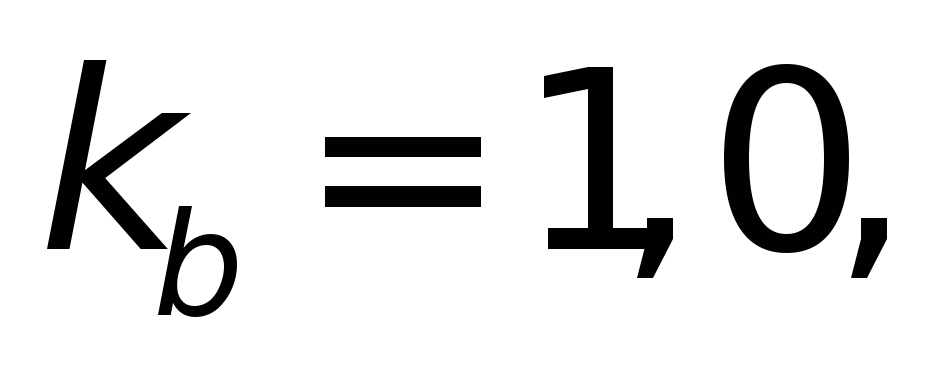
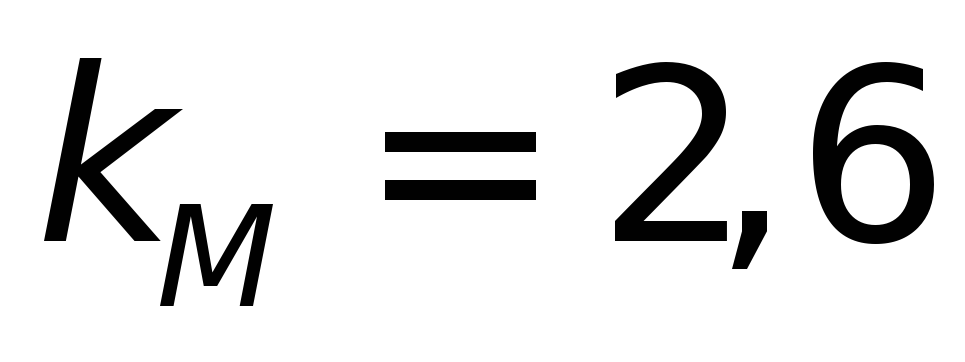 и
и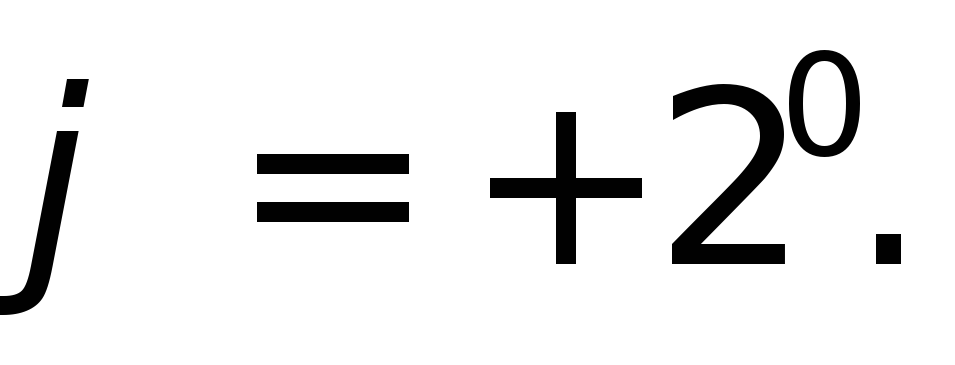
Вычисляем элементы среднего квадратического эллипса погрешностей:
![]()
![]()
Линию большой оси эллипса погрешностей откладываем от более точной линии положения
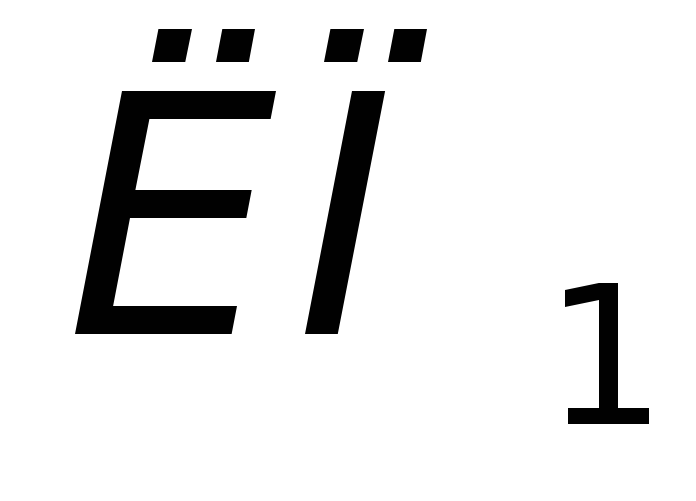 под углом
под углом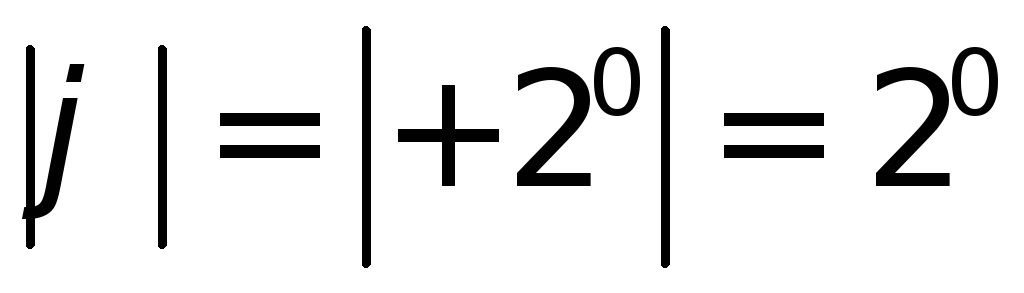 внутрь угла между линиями положения,
равного
внутрь угла между линиями положения,
равного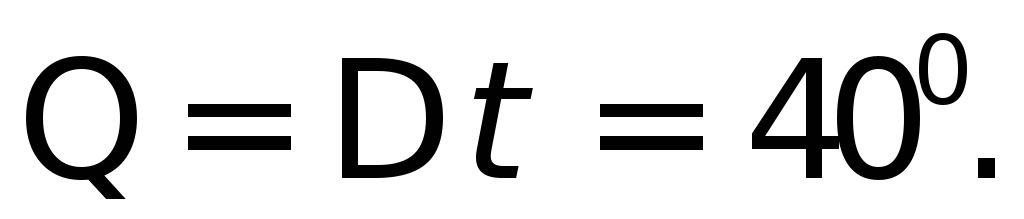
Вычисляем радиальную СКП места:
![]()
Пример.
Полные СКП линий
положения
![]() и
и![]() Коэффициент взаимной корреляции
Коэффициент взаимной корреляции![]() Направления градиентов линий положения
Направления градиентов линий положения![]() и
и![]() Определить эллиптическую и радиальную
средние квадратические погрешности
места, а также их предельные значения
для вероятности
Определить эллиптическую и радиальную
средние квадратические погрешности
места, а также их предельные значения
для вероятности![]()
Решение.
По
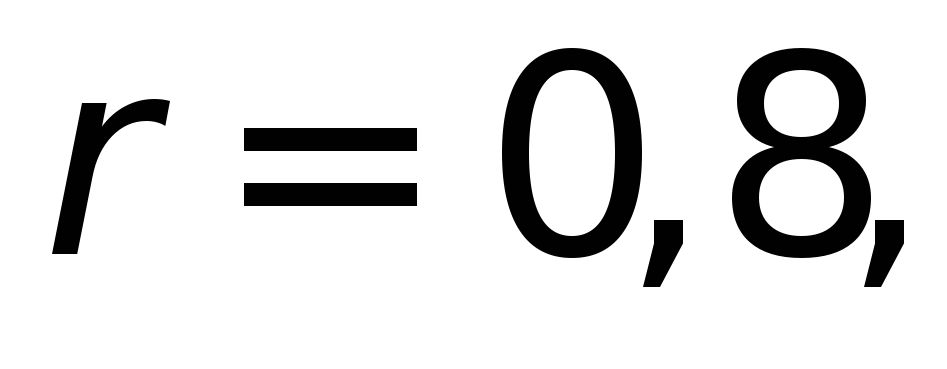
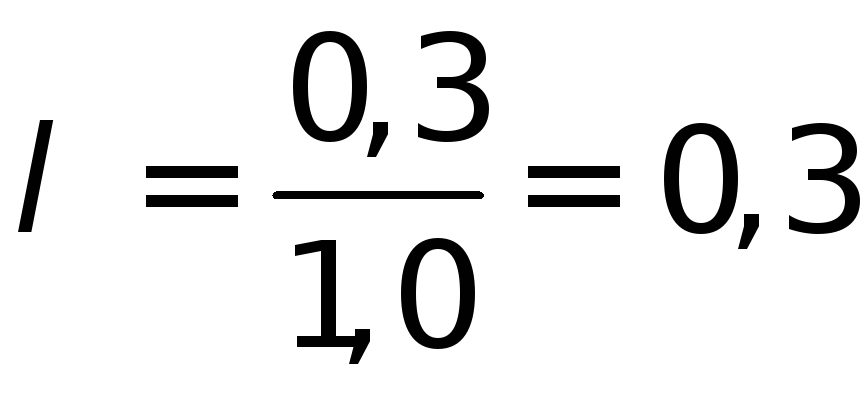 и
и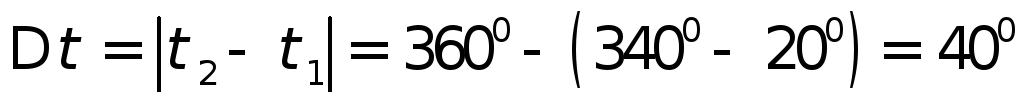 из табл.4.11д выбираем
из табл.4.11д выбираем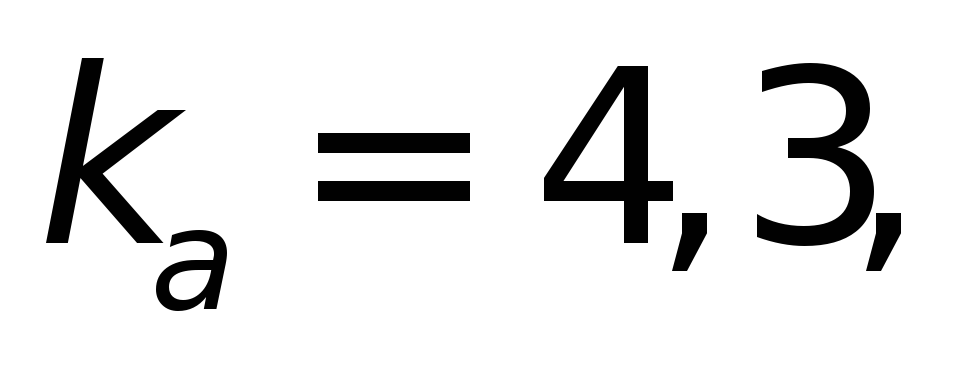
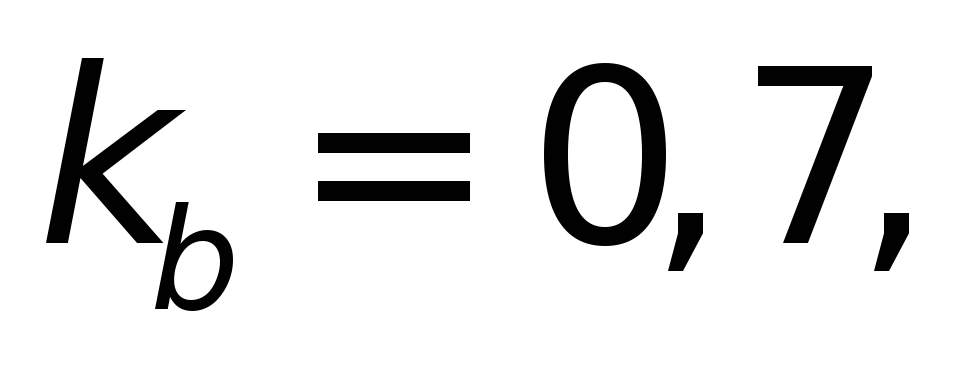
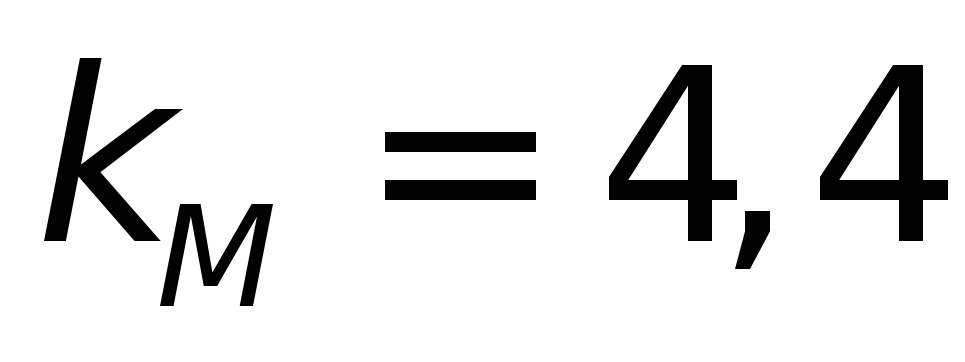 и
и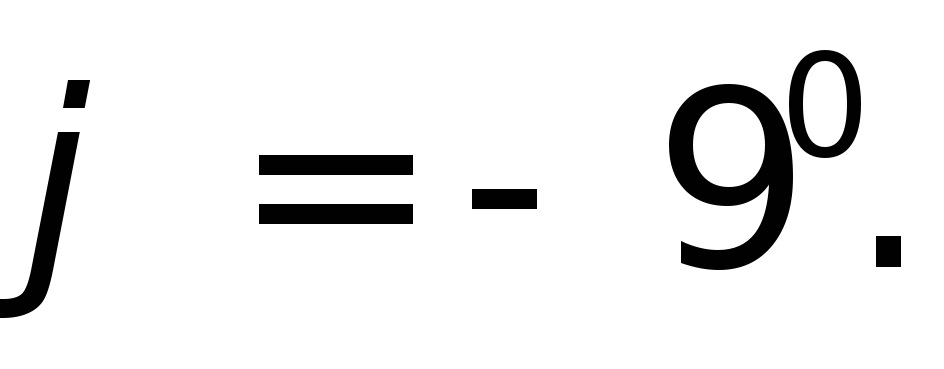
Вычисляем элементы среднего квадратического эллипса погрешностей:
![]()
![]()
Линию большой оси эллипса погрешностей откладываем от более точной линии положения
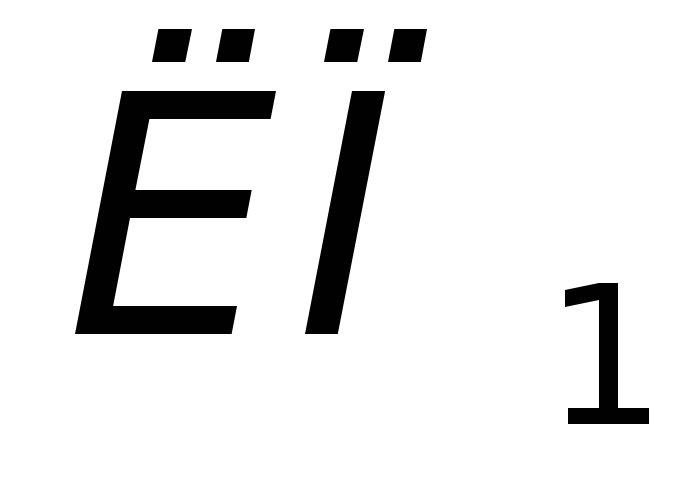 под углом
под углом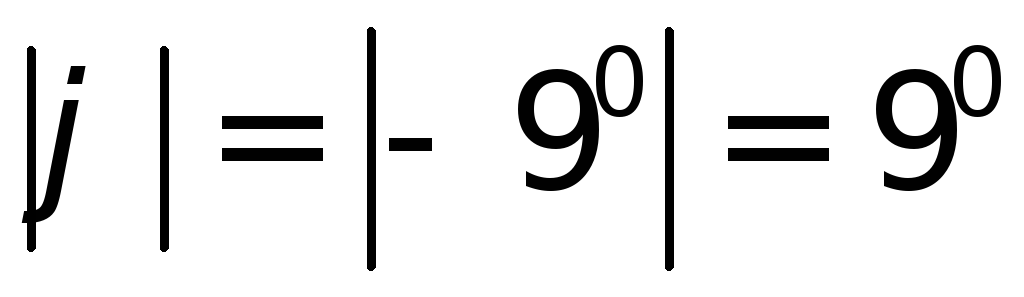 внутрь угла между линиями положения,
равного
внутрь угла между линиями положения,
равного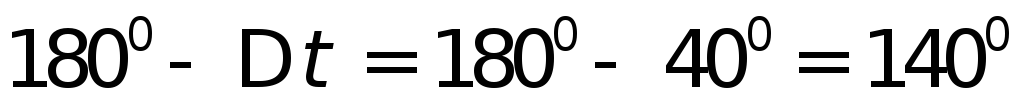 (т.к.
угол
(т.к.
угол отрицательный).
отрицательный).Вычисляем радиальную СКП места:
![]()
По заданной вероятности
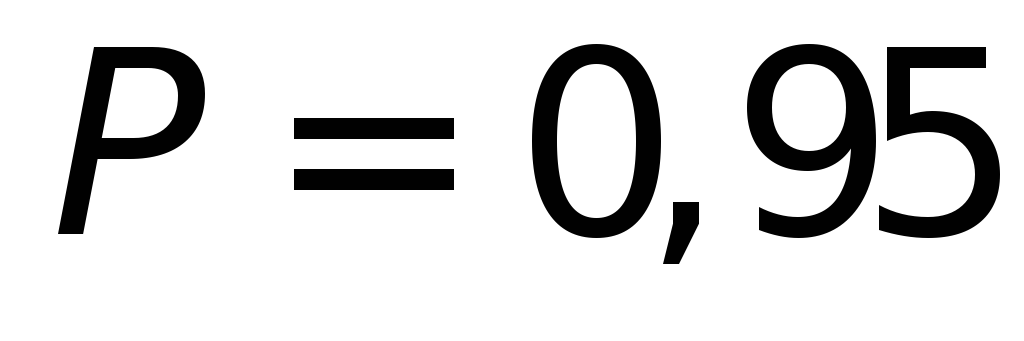 из табл. 4.12 выбираем коэффициент
из табл. 4.12 выбираем коэффициент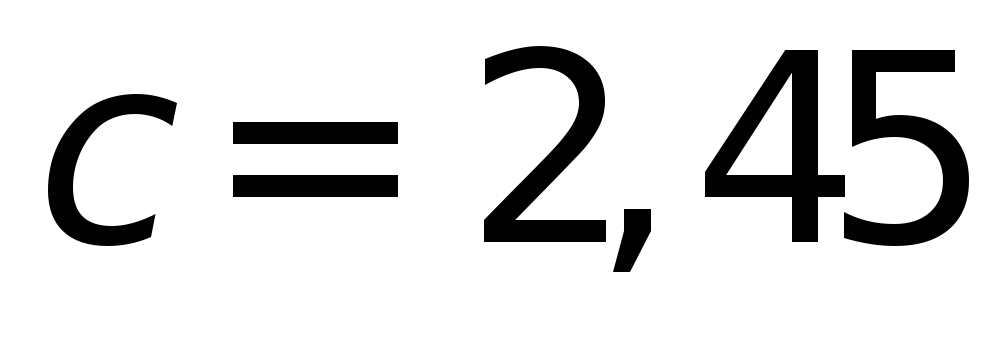 и вычисляем элементы предельного
эллипса погрешностей
и вычисляем элементы предельного
эллипса погрешностей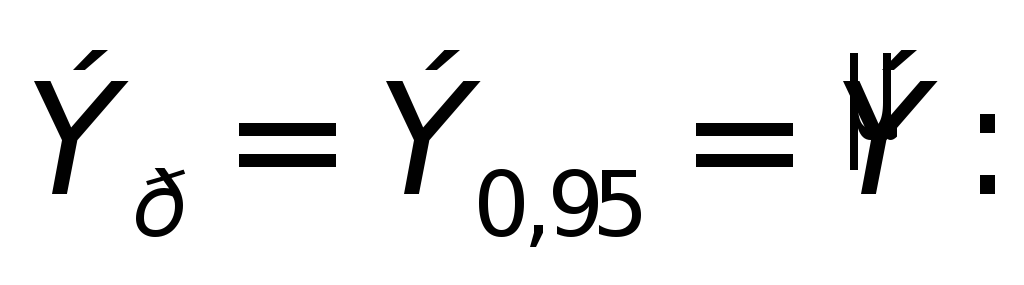
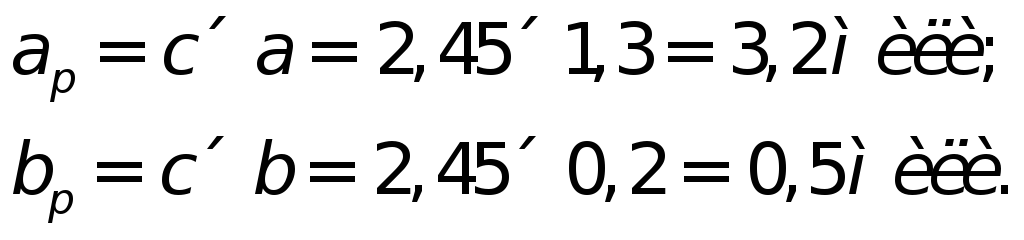
По заданной вероятности
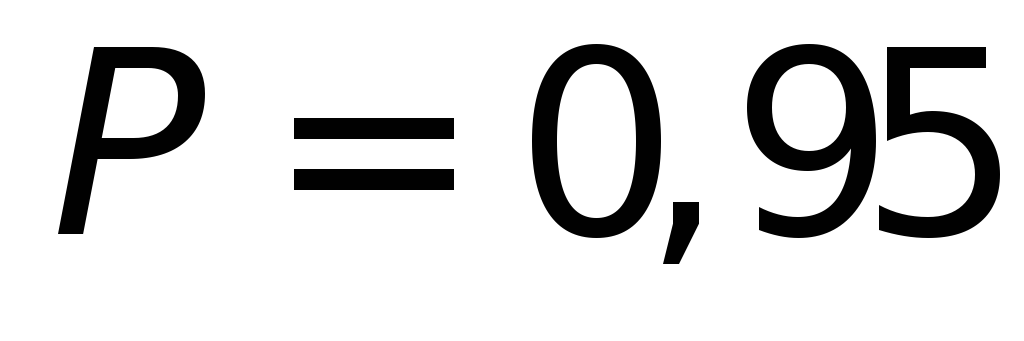 и отношению полуосей
и отношению полуосей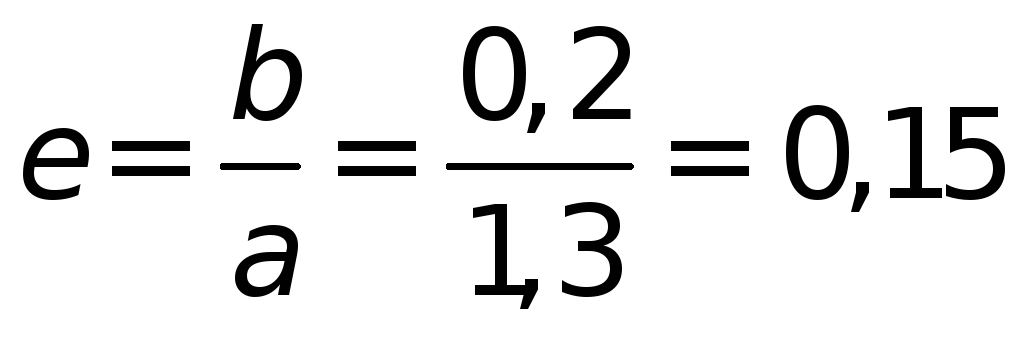 из табл. 4.14 выбираем коэффициент
из табл. 4.14 выбираем коэффициент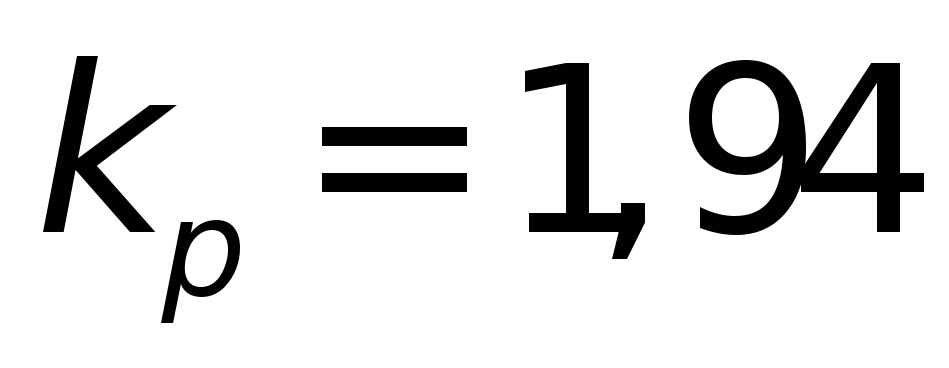 и вычисляем радиальную предельную
погрешность
и вычисляем радиальную предельную
погрешность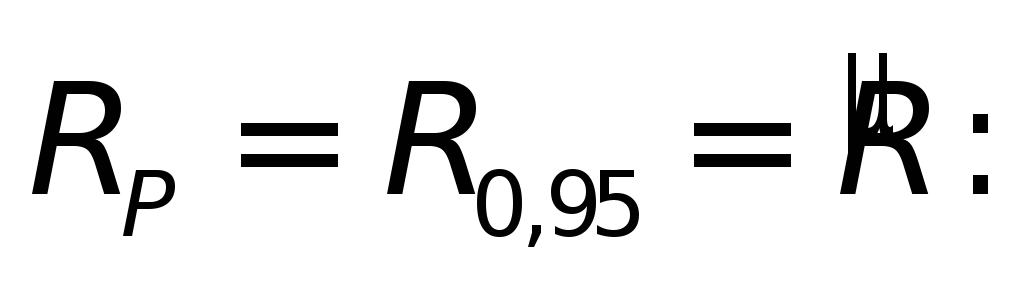
![]()