методичка_1 / гл4

Глава 4

Глава 4.

Описательная статистика

Откройте программу Excel. Если Вы выполняли задания по информатике раньше и сохранили свой файл, откройте его. Задание выполняйте на новом листе. Введите его название: описательная статистика. В ячейку А1 введите дату выполнения работы, в ячейку А2 – факультет и номер группы, в ячейку А3 – фамилии студентов, выполняющих работу. В конце работы в названии файла укажите группу и фамилии студентов и сохраните файл.

Теория

Описательная статистика сжато описывает полученные статистические данные для какой-либо выборки. Если известна выборка: х₁, х₂, ..., х_n, где n – объем выборки, то можно рассчитать ее характеристики. К ним относятся:

выборочное среднее ,

исправленная выборочная дисперсия ,

выборочное среднеквадратическое отклонение ,

Можно также рассчитать полуширину доверительного интервала для генерального среднего

, (*)

где t – коэффициент Стьюдента,  – доверительная вероятность, f = n – 1 – степень свободы.

Для расчета этих параметров воспользуйтесь статистическими функциями Excel:

- для нахождения выборочного среднего используется функция СРЗНАЧ,

- для исправленной выборочной дисперсии – ДИСП,

- для выборочного среднеквадратического отклонения – СТАНДОТКЛОН (выборочное среднеквадратическое отклонение принято называть стандартным отклонением),

- для нахождения коэффициента Стьюдента используется функция СТЬЮДРАСПОБР.

Эти функции вызываются, если щелкнуть мышью по виртуальной кнопке f_x (см. рис. 4.1).

Рис. 4.1

Для функций СРЗНАЧ(Х), ДИСП(Х) и СТАНДОТКЛОН(Х) в качестве параметра Х задаются адреса ячеек, в которые занесены исходные данные выборки.

У функции СТЬЮДРАСПОБР(вероятность; степени свободы) два параметра. Чтобы задать параметр степени свободы надо воспользоваться формулой f = n – 1, т.е., если объем выборки равен 10, то степень свободы равна 9. Чтобы задать параметр вероятность надо знать доверительную вероятность . Она должна быть задана. Обычно берется значение  = 0.95. Тогда параметр вероятность вычисляется по формуле р = 1 – . Если доверительная вероятность равна 0.95, то параметр вероятность, который надо задать в функции СТЬЮДРАСПОБР, равен 0.05.

Примечание. Данные для заданий 1-4 взяты из книги С.Гланца «Медико-биологическая статистика».

Задание 1. Исследовали быстроту выведения кофеина у мужчин. У 13 испытуемых измеряли период полувыведения кофеина (время уменьшения концентрации вдвое). Результаты измерений представлены в таблице:

Период полувыведения кофеина (в часах)
2,04
5,16
6,11
5,82
5,41
3,51
3,18
4,57
4,83
11,34
3,79
9,03
7,21

1) Найдите выборочное среднее, исправленную выборочную дисперсию, выборочное среднеквадратическое отклонение.

2) Определите доверительные интервалы, в которых находится генеральное среднее, (т.е. усредненное значение периода полувыведения кофеина у мужчин) при разных доверительных вероятностях ₁ = 0.9, ₂ = 0.95, ₃ = 0.99.

3) При каком значении доверительной вероятности (₁, ₂ или ₃) коэффициент Стьюдента максимальный? Как меняется полуширина доверительного интервала при изменении доверительной вероятности?

Выполнение задания:

1) При оформлении задания удобно вычисление каждой требуемой величины размещать в ячейке ниже полного названия величины. Например (см. рис. 4.2), ячейка С2 содержит название среднее значение, ячейка С3 содержит функцию расчета = СРЗНАЧ(А3:А15).

Рис. 4.2

Чтобы название умещалось в ячейке, можно изменить ее горизонтальный или вертикальный размеры. Это можно сделать с помощью мыши. Например, если поместить курсор на поле названий столбцов на границе между столбцами и нажать левую клавишу, то, двигая мышь, горизонтальный размер столбца можно менять.

2) Для получения доверительного интервала требуется задать n – количество данных. Для этого в ячейке, например, E2 задайте название, а в ячейке E3 число n (в нашем случае 13).

Дополнительно. Количество данных можно пересчитать с помощью функции =СЧЁТ(A3:A15); пустые ячейки и названия будут пропущены. (Если не вводить адреса ячеек, то автоматически будет посчитано количество данных, но не Ваших, а находящихся во всех ячейках, расположенных слева в строке или сверху в столбце).

В ячейки G3, G4 и G5 внесем значения γ: 0,9 ;0,95; 0,99. В ячейку G2 введем греческую букву γ, используя меню Excel: Вставка – Символ – γ – Вставить – Закрыть. Задайте формулу (*) в ячейке E3, для вычисления полуширины доверительного интервала. (См. подсказки на рис. 4.3). Сделать это надо и в ячейках Е4, Е5 для каждого значения γ. Чтобы не вводить одинаковые формулы трижды, выделяем ячейку Е3, правой клавишей мыши вызываем меню – Копировать. Далее выделяем ячейки Е4 и Е5, заходим на них мышью. Вызываем меню – Вставить и обязательно нажимаем Enter.

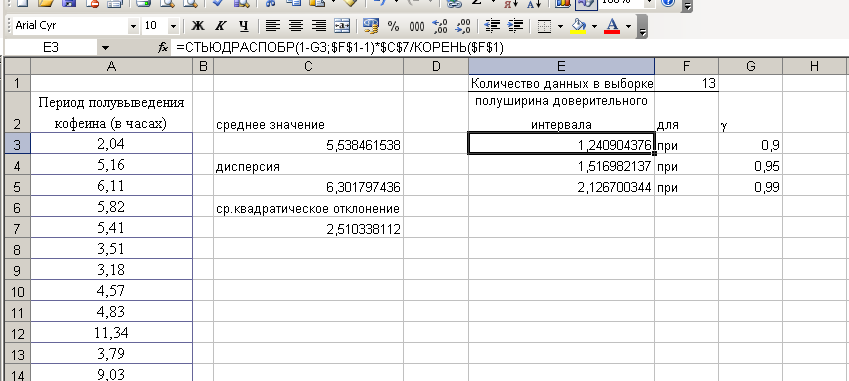
Рис. 4.3

Ответ можно оформить как двойное неравенство, рассчитав значения и ( находится в ячейке С3, – в ячейках Е3:Е5). Результат может выглядеть так, как на рис. 4.3. Чтобы отбросить лишние десятичные знаки числа, можно поступить следующим образом. Выделив ячейку с этим числом, правой кнопкой мыши вызвать меню, выбрать Формат ячеек – Числовой – Число десятичных знаков – 2, ОК.

Обратите внимание, что в ячейках Excel может находиться разное содержимое: число (например, в G3), текст (в Е2) или формула (в Е18). Число расположено в ячейке справа. Расположение текста зависит от формата ячейки, обычно текст расположен слева. Чтобы разместить несколько строк в одной ячейке (как в С16), надо: в Формате ячейки указать Выравнивание – по вертикали: Распределенный.

Дополнительно. Если нужно перенести уже рассчитанные данные в другое место Листа Excel или на другой Лист, то пользуются Специальной вставкой. Предположим, надо перенести результаты расчетов доверительных интервалов, которые находятся в ячейках Е3:Е5 в ячейки G21:G23. Выделяем ячейки Е3:Е5, заходим мышью на выделенную область, вызываем меню, жмем Копировать. Выделяем ячейку G21, из ячейки G21 вызываем меню (см. рис.4.4 и 4.5), выбираем Специальная вставка, Вставить – значения и форматы чисел, ОК. После такой вставки содержимым ячейки становится нужное число.

Рис. 4.4

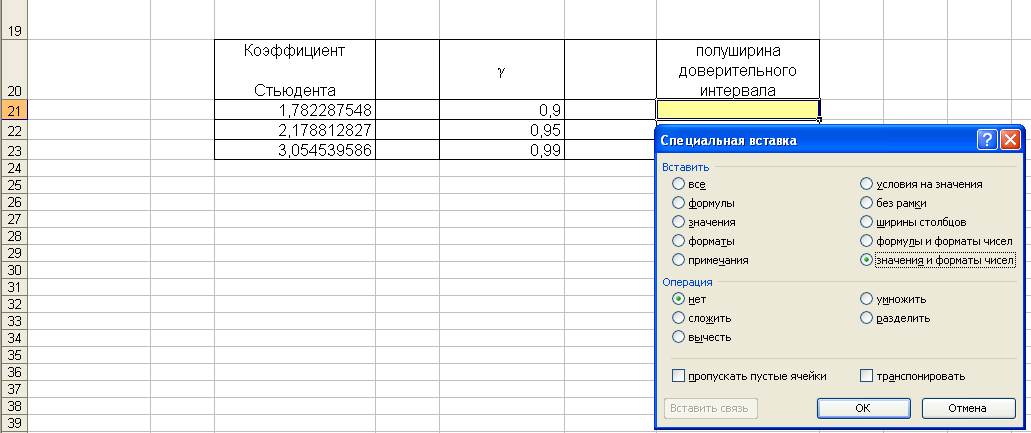
Рис. 4.5

Задание 2а. Исследовали влияние безникотиновых сигарет на работу сердца. На 12 испытуемых с болезнью сердца измеряли продолжительность физической нагрузки до появления одышки. Тест проводился два раза: до курения безникотиновых сигарет и после. Результаты измерений представлены в таблице:

Длительность нагрузки до появления одышки (в секундах)

курение безникотиновых сигарет
до	после
289	155
203	117
359	187
243	134
232	135
210	119
251	145
246	121
224	136
239	124
220	118
211	107

Найдите выборочные средние, исправленные выборочные дисперсии, выборочные среднеквадратические отклонения. Определите доверительные интервалы, в которых находятся генеральные средние с доверительной вероятностью 0,95.

Задание 2б. На тех же испытуемых исследовали влияние вдыхания окиси углерода на работу сердца. Проводили те же измерения до и после вдыхания окиси углерода. Результаты измерений представлены в таблице:

Длительность нагрузки до появления одышки (в секундах)

вдыхание окиси углерода
до	после
281	177
186	125
372	238
254	165
219	153
225	148
264	180
237	144
212	152
250	147
209	138
226	141

Найдите выборочные средние, исправленные выборочные дисперсии, выборочные среднеквадратические отклонения. Определите доверительные интервалы, в которых находятся генеральные средние с доверительной вероятностью 0,95.

Задание 3. На собаках исследовали возможность использования некоторого лекарства Н при поражении сердца, вызванном кокаином. Двадцать две собаки разделили на две равные группы и вводили им кокаин. Затем одной группе вводили лекарство Н, а другой – физиологический раствор (плацебо). Измеряли среднее артериальное давление и диаметр коронарной артерии. Результаты измерений представлены в таблице:

Среднее артериальное давление, мм рт.ст.		Диаметр коронарной артерии, мм
плацебо	лекарство Н	плацебо	лекарство Н
156	73	2,5	2,5
171	81	2,2	1,7
133	103	2,6	1,5
102	88	2,0	2,5
129	130	2,1	1,4
150	106	1,8	1,9
120	106	2,4	2,3
110	111	2,3	2,0
112	122	2,7	2,6
130	108	2,7	2,3
105	99	1,9	2,2

Для всех четырех наборов данных найдите выборочные средние, исправленные выборочные дисперсии, выборочные среднеквадратические отклонения, определите доверительные интервалы, в которых находились (с доверительной вероятностью  = 0.95) генеральные средние.

Задание 4. В клинике Вашингтонского университета исследовали расходы пациентов на обследование и последующее лечение. В конечном счете, расходы пациента определяются лечащим врачом. В исследовании участвовали 13 врачей: их частично информировали о том, какие расходы несут пациенты их коллег. Для каждого врача определяли среднегодовые расходы на обследование и лечение одного пациента до и после ознакомления с расходами пациентов их коллег. Результаты представлены в таблице:

среднегодовые расходы на обследование одного пациента, доллары		среднегодовые расходы на лечение одного пациента, доллары
до ознакомления	после ознакомления	до ознакомления	после ознакомления
20	20	32	42
17	26	41	90
14	1	51	71
42	24	29	47
50	1	76	56
62	47	47	43
8	15	60	137
49	7	58	63
81	65	40	28
540	9	64	60
48	21	73	87
55	36	66	69
56	30	73	50

Для всех четырех наборов данных найдите выборочные средние, исправленные выборочные дисперсии, выборочные среднеквадратические отклонения, определите доверительные интервалы, в которых находились (с доверительной вероятностью  = 0.95) генеральные средние.

Задание 5. Приведены результаты измерений систолического давления (в мм рт. ст.) у жителей города N:

Данные для Задания 5а

119	110	147	124	132
118	123	135	133	134
107	109	122	134	120
121	132	124	113	115
123	121	125	127	106

Данные для Задания 5б

121	111	147	124	132
128	123	138	133	134
115	145	132	144	120
123	132	126	113	133
123	121	125	128	116

Данные для Задания 5в

121	143	157	124	132
128	115	143	133	134
156	130	132	134	157
123	128	126	145	134
123	121	125	118	141

Данные для Задания 5г

151	143	147	164	132
128	165	133	133	134
156	155	132	134	157
163	132	146	145	134
123	131	125	134	141

Данные для Задания 5д

121	143	147	134	151
176	165	163	143	155
156	155	162	154	157
163	122	146	145	134
178	189	165	154	141

Данные для Задания 5е

141	166	157	164	151
176	165	163	176	155
156	165	162	154	157
163	178	166	165	187
178	189	165	154	131

Оценить параметры систолического давления жителей города N (генеральное среднее, генеральную дисперсию и генеральное среднеквадратическое отклонение).

Для доверительной вероятности 0,95 дать интервальную оценку для генерального среднего систолического давления у жителей города N.

Задание 6. Используя функцию СТЬЮДРАСПОБР, составьте таблицу для значений коэффициента Стьюдента такую же, как в учебнике Основы высшей математики и статистики Морозова Ю. В.

Окончание работы.

После выполнения заданий сохраните файл в папке ИНФОРМАТИКА. Лечебный факультет под именем, содержащим номер группы и фамилии тех, кто выполнял работу. Например, 92гр.Иванов,Петров

Контрольные вопросы к занятию по информатике:

Описательная статистика.

1. Какую информацию об исследуемой величине несут выборочные характеристики: выборочное среднее, исправленная выборочная дисперсия, выборочное среднеквадратическое отклонение?

2. От чего зависит полуширина доверительного интервала для генерального среднего?

3. Как меняется полуширина доверительного интервала при изменении доверительной вероятности?

4. Как влияет на коэффициент Стьюдента изменения объема выборки и доверительной вероятности?

1. Морозов Ю.В. Основы высшей математики и статистики. М. Медицина 1998 стр. 140-144

2. В.Ф.Антонов и др. Физика и биофизика. Практикум 2008 стр. 8-14

51