методичка_1 / гл2

Глава 2

Глава 2.

Нормальный закон распределения. Функция Гаусса.

Откройте программу Excel. Если Вы выполняли задания по информатике раньше и сохранили свой файл, откройте его. Задание выполняйте на новом листе. Введите его название: нормальный закон распределения. В ячейку G1 введите дату выполнения работы, в ячейку G2 – факультет и номер группы, в ячейку G3 – фамилии студентов, выполняющих работу.

Задание 1. а) Построить на одной диаграмме на интервале х є [-4; 4] с шагом 0,1 три графика при разных значениях параметров µ и :

1) µ = 0 и  = 1,

2) µ = 1 и  = 0.5,

3) µ = 1 и  = 2.

б) определить, как меняется вид графика при изменении параметров µ и .

в) определить x и y координаты максимума и точек перегиба функции f(x).

Нормальный закон распределения плотности вероятности f(x) непрерывной случайной величины x описывается выражением (функцией Гаусса): .

Рис. 2.1

Выполнение задания. Для вычисления f(x) используйте математические функции КОРЕНЬ(Х) и EXP(X) = e^x. Значения параметров µ и  задайте в отдельных ячейках.

Столбец для х заполните заданными значениями (начиная с –4, используя набор команд Правка — Заполнить — Прогрессия). Для заполнения столбца значений f(x) введите формулу в одну ячейку и используйте Копировать и Вставить.

Внимание. При построении графиков в программе Мастер диаграмм следует пользоваться типом диаграммы: точечная. Именно этот тип диаграммы позволяет построить изображение в масштабе по обеим осям (см. рис. 2.2).

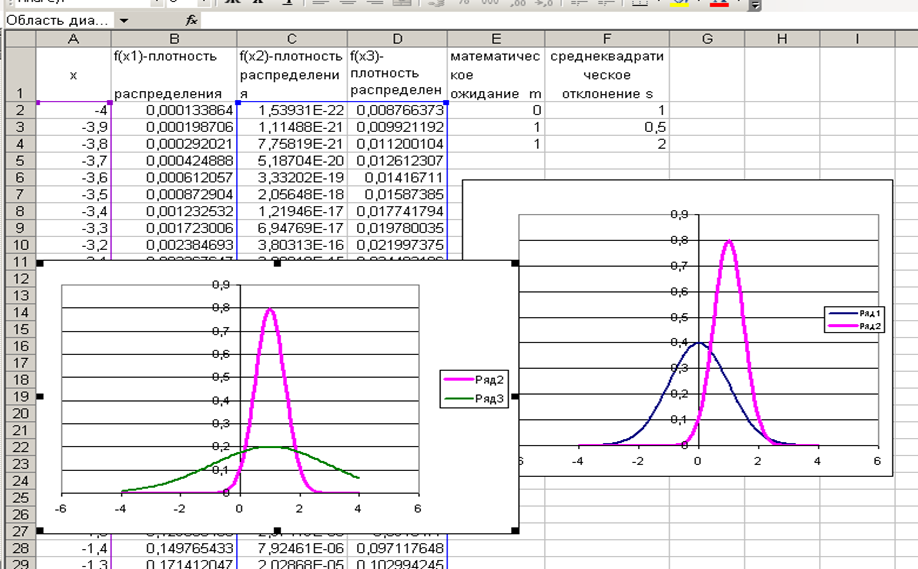
Рис. 2.2.

Задание 2. Выполнить построение графиков задания 1, вычисляя функцию плотности распределения с помощью статистической функции НОРМРАСП. Сравнить полученные результаты.

Выполнение задания. Задание выполняйте на новом листе. Введите его название: нормальный закон распределения(2).

В Excel существует специальная статистическая функция с четырьмя параметрами НОРМРАСП( x, среднее, стандартное откл, интегральная) для расчета нормального закона распределения. Первые три параметра используются в функции Гаусса. Для четвертого параметра справка Excel дает следующую информацию: интегральная – это логическое значение, определяющее форму функции. Если интегральная имеет значение ИСТИНА, то функция НОРМРАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения. Функция плотности распределения – это и есть функция Гаусса (см. рис. 2.3).

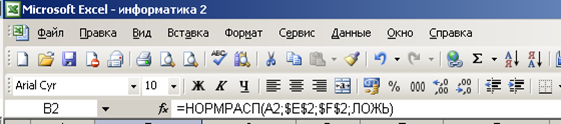
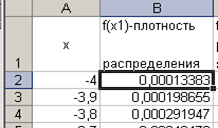
Рис. 2.3

Для задания статистической функции НОРМРАСП используйте Мастер функций. В окне Аргументы функции в строке интегральная наберите слово ложь. Выглядеть это должно примерно так, как на рис. 2.4. При выделении ячейки, содержащей формулу, Excel показывает связи ячеек:

Рис. 2.4.

Задание 3. Даны три случайные величины Х₁, Х₂ , Х₃, распределенные по нормальному закону с разными значениях параметров μ и 

для Х₁ μ = 0,  = 1;

для Х₂ μ = 1,  = 0,5;

для Х₃ μ = 1,  = 2.

Для всех трех величин рассчитать вероятности того, что они лежат в интервалах от μ- до μ+, от μ-2 до μ+2 и от μ-3 до μ+3.

Внимание. Для нахождения вероятности P(a < x < b) того, что случайная величина x, распределенная по нормальному закону со средним значением μ и среднеквадратическим отклонением  лежит в интервале от а до b, необходимо вычислить интеграл: . Этот интеграл можно представить в виде разности интегралов , а интеграл задается в Excel с помощью функции НОРМРАСП с четвертым параметром интегральная ИСТИНА. Таким образом, вероятность вычисляется как разность

P(a < x < b) = НОРМРАСП( b, μ, , истина) —

— НОРМРАСП( а, μ, , истина)

Задание 4а. Предположим, что длительность цикла работы сердца распределена по нормальному закону. Построить кривую распределения плотности вероятности для длительности цикла работы сердца (в секундах). Необходимые параметры задать самостоятельно. Рассчитать вероятность того, что длительность цикла лежит в интервале от 0,7 до 0,9 с.

Задание 4б. Предположим, что длительность дыхательного цикла распределена по нормальному закону. Построить кривую распределения плотности вероятности для длительности дыхательного цикла (в секундах). Необходимые параметры задать самостоятельно. Рассчитать вероятность того, что длительность цикла лежит в интервале от 3 до 5 с.

Задание 5а. Предположим, что рост мужчин и рост женщин распределены по нормальному закону. Построить на одной диаграмме две кривые распределения плотности вероятности для роста мужчин и женщин. Необходимые параметры задать самостоятельно.

Задание 5б. Предположим, что систолическое давление у здоровых людей и у людей с диагнозом гипертония распределены по нормальному закону. Построить на одной диаграмме две кривые распределения плотности вероятности для систолического давления. Необходимые параметры задать самостоятельно.

Задание 5в. Предположим, что размеры (в см) грудной клетки, грудной клетки на вдохе и на выдохе у взрослых мужчин распределены по нормальному закону. Построить на одной диаграмме три кривые распределения плотности вероятности для размера грудной клетки, грудной клетки на вдохе и на выдохе у взрослых мужчин. Необходимые параметры задать самостоятельно.

Задание 5г. Предположим, что рост школьников, студентов и баскетболистов распределены по нормальному закону. Построить на одной диаграмме три кривые распределения плотности вероятности для роста школьников, студентов и баскетболистов. Необходимые параметры задать самостоятельно.

Окончание работы.

После выполнения заданий сохраните файл в папке ИНФОРМАТИКА под именем, содержащем номер группы и фамилии тех, кто выполнял работу. Например, 92гр.Иванов,Петров

Контрольные вопросы к занятию по информатике:

Нормальный закон распределения. Функция Гаусса.

1. Нормальный закон распределения плотности вероятности непрерывной случайной величины.

2. График функции Гаусса .

3. Координаты максимума и точек перегиба функции.

4. Параметры нормального закона распределения: математическое ожидание µ (среднее значение) и среднеквадратическое отклонение .

5. Как меняется график функции плотности вероятности при изменении параметров µ и ?

6. Чему равна вероятность того, что случайная величина, распределенная по нормальному закону, лежит в интервалах а) [ µ - 3 ; µ + 3 ], б) [ µ -2 ; µ +2], в) [ µ - ; µ + ]?

7. Правило трех сигм ().

Литература

Морозов Ю.В. Основы высшей математики и статистики. М. Медицина, 1998

Стр.124 - 128

26