Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Первый московский государственный медицинский университет им. И.М. Сеченова

Предмет:

Математика

Файл:

metodichka_Fedorovoi-_matanaliz_diffur / Т е м а 1

.pdf

Скачиваний:

Добавлен:

09.02.2015

Размер:

315.33 Кб

Скачать

☆

Т е м а 1

Производная функции одной переменной

Понятие производной - одно из основных понятий математического анализа. Производная характеризует быстроту изменения функции при изменении ее аргумента. В частности, производные применяются при математическом описании кинетики химических реакций, динамики движения, при нахождении градиента скорости, давления, температуры и других величин.

Литература для подготовки к занятию по теме: Ю.В.Морозов "Основы высшей математики и ста-

тистики", М., 1998, с.19-28, 37-50.

В процессе подготовки к практическому занятию по теме необходимо выполнить следующее:

1. Повторить следующие теоретические вопросы:

1)Понятие функции.

2)Понятие предела функции (аналитическая форма записи предела функции в точке)

II. Изучить по указанной литературе следующие вопросы:

1)Понятие производной функции.

2)Физический смысл производной (привести примеры на вычисление скорости и градиента).

3)Геометрический смысл производной (пояснить

спомощью графика).

4)Основные формулы дифференцирования - производная постоянной, степенной, экспоненциальной, логарифмической, тригонометрических функций. Таблицу производных этих функций необходимо перенести в рабочую тетрадь.

5)Правила дифференцирования алгебраической суммы, произведения, частного двух функций.

6)Понятие сложной функции.

7)Правило дифференцирования сложных функций (пояснить на примере, как выбирается промежуточная переменная).

Эталоны решения типовых задач и задачи для самоконтроля

Задача 1. Вычислить производную функции y 5x4

Решение Данное выражение является степенной функцией

вида

y xn , умноженной на постоянный коэффициент. В соответствии с правилом дифференцирования функции, умноженной на константу, постоянный коэффициент можно выносить за знак производной, поэтому:

y 5 (x4 )

	Далее		в соответствии		с формулой (xn ) n xn 1 ,
получим:
			y 5 4x4 1 20x3
	Найти		самостоятельно		производную	функции
y	1	x5 .
y	5	x5 .
	5
	Задача		2.	Найти	производную	функции

y x12 x 2

Решение Для решения задачи необходимо применить пра-

вило дифференцирования алгебраической суммы:

(U V W ) U V W

и формулу производной степенной функции. Тогда получим:

	1				2
					2
y	( x2	x	2)	(x		)	(x)	(2)
y	( x2	x	2)	(x		)	(x)	(2)
или y 2x 2 1		x1 1	0 2x 3				1		2	1
или y 2x 2 1		x1 1	0 2x 3				1		x3	1
									x3

Здесь при вычислении производной первого слагаемого суммы и записи результата использована

возможность представления дроби x 2 в виде степен-

ной функции с отрицательным показателем степени:

1	x 2	(в
x 2

степенной степени в мого равна

общем случае	1	x n ), и наоборот -
	x n

функции с отрицательным показателем виде дроби. Производная второго слагае- - 1, производная константы равна нулю.

y ( x12 x 2) x23 1

Найти самостоятельно производные следующих функций:

1.y x3 x 6

2.y x13 1x 1

Задача 3. Найти производную функции y 3 x2 Решение

Для решения задачи необходимо сначала представить эту функцию в виде степенной функции с

дробным показателем степени, по формуле: n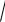xm x n

													2

			В нашем случае имеем: y 3 x2										x 3
			Далее, применив правило дифференцирования
степенной							функции, с показателем степени											n	2	,
степенной							функции, с показателем степени											n		,
																		3
найдем:
		2 (		2	1)	2			1		2
		2 (			1)	2					2

y	3 x			3		3 x			3		33
y	3 x			3		3 x			3		33	x
			Найти самостоятельно производные следующих
функций:
						y 55							y	1
	1.									x2	3.			1


														3		x
														3		x
						y	1						y		1
	2.						1				4.

														73			x 2
								x
								x

Задача 4. Найти производную функции y e x sin x Решение

Данная функция является произведением экспоненциальной функции е и тригонометрической функции sin x .

Применяя правило дифференцирования произведения функций и используя правила дифференцирования

функций e x

sin x , найдем

производную

произведе-

ния

sin x) (e

sin x cos x e

(sin x cos x)

)

sin x (sin x) e

Найти самостоятельно производные функций :

1)y x2 cos x

2)y x ex

3)y x3 (sin x 1)

4)y x2 ln x

Задача 5. Найти производную функции

Решение Применяя формулу дифференцирования

функций:

U
U					U V UV

					V 2
V					V 2

y ln x 2 x

частного

и основные формулы дифференцирования, полу-

чим:

(

0) x (ln x 2) 1

(

ln x 2

)

(ln x 2)

x (ln x 2)

1 ln x 2

3 ln x

Найти самостоятельно производные функций

cos x

ln x

e x

e x 1

sin x

ln x

Доказать, что

производная функции

y ctgx

равна	(	1		)

		sin 2
			x

Задача 6. Найти производную функции y sin 2x .

Решение Данная функция отличается от табличной множи-

телем а=2 при переменной х. Производная пишется по правилу дифференцирования сложной синусоидальной функции

(sinU ) cosU U

Применяя правило дифференцирования сложной синусоидальной функции, получим:

y (sin 2x) (cos 2x) 2 2 cos 2x

Найти самостоятельно производные функций:

1.y sin(x2 1)

2.y cos(2x 1)

Задача 7.

Найти	производную функции y eax , где а -
константа.

Решение.

Данная функция отличается от табличной множителем "а" при переменной х и является сложной.

Применяя правило дифференцирования сложной экспоненциальной функции

(eax ) eax (ax) , получим:

(eax ) eax (ax) aeax

Найти самостоятельно производную функции:

1. y e5x
		2. y e x

Задача	8. Найти производную функции y		x3 2
		Решение
Данная	функция может быть представлена в виде

сложной степенной

y(x3 2) 2

Всоответствии с формулой производной сложной степенной функции

(U n ) nU n 1 U

в данном случае имеем:

	1	1			1	1			3x		2
	1				1						2
y (x3 2)	2		(x3	2) 2			(x3 2)
	2	2
								2		x3 2
								2		x3 2

Найти самостоятельно производные сложных функций:

1.y 13 cos 3x

2.y e x2

3.y 1 ln x

Задача 9. Точка совершает колебания по закону

S S sin( t 4 ) , где S = 2 (м). Определить скорость

тела в момент времени t 14 с.

Решение

Скорость тела в любой момент времени t определяется производной S (t) . Функция S(t) является сложной функцией.

Применяя формулу дифференцирования сложной функ-

ции, в нашем случае получим

(sinU ) cosU U

) ( t

)

S cos( t

)

v(t) S (t) S cos( t

Скорость тела в момент времени

с есть

) S (

) 2 cos(

4 ) 2 cos

2 0

Ответ: скорость тела

момент

времени t

равна нулю.

Задание. Определить самостоятельно ускорение

тела в

момент

времени

с, если

скорость тела

v(t) 2 cos( t )

и измеряется в м/с.

Задача 10. Определить величину градиента концентрации, если зависимость концентрации от коор-

динаты задана функцией C(x) C e kx , где k - кон-

станта, а C - есть концентрация вещества при x 0 .

Решение Величина градиента определяется выражением

C (x) dCdx и характеризует быстроту изменения кон-

центрации при изменении координаты.
Пользуясь			правилом	дифференцирования			сложной
функции
			(eU ) eU U
в данном случае получим:
	dC	C e kx	( kx) k C	e kx
		C e kx	( kx) k C	e kx
	dx
		Ответ: градиент концентрации			dC	k C	e kx
		Ответ: градиент концентрации			dx	k C	e kx
					dx

Решить самостоятельно задачу:

При ламинарном течении вязкой жидкости в трубе слои жидкости имеют различную скорость в зависимости от расстояния x от оси трубы.

v(x) P (R2 x2 ) ,

4 l

где P - разность давлений на участке трубы длиной l

R- радиус трубы,

- коэффициент вязкости.

Найти величину градиента скорости на расстоянии x от оси трубы.

Задачи для решения на практическом занятии

1. y 3x2 2					16.	y 4 x2 sin x
1		1

2. y				x	17.	y 8cos(3t 3 )
	x3		x
3. y sin x ctgx					18.	y 5ln(2x 3)
4. y	ln x				19.	y 3sin(t )

	x					2
5. y	5x				20.	y e 3x cos 5x
	ln x

6. y sin 2 4x

21.

y cos5 3x

y esin2 x

7. y

22.

8. y sin e x

23.

e 3x

9. y

esin x

24.

y ln sin x

cos 2x

y cos e x

10.

25.

x2 a2

11.

y ln

1 x

26.

y e4 x

1 x

12.

y 5sin(3x 2)

27.

x 2

13.

y 5 e x2

28.

y Ae t

cos(wt )

y 0.5 e 2 x

14.

y x

1 x2

29.

15.

y 3cos 2 x

30.

y ctgx tgx

31) Найти скорость изменения во времени концентрации C лекарственного вещества при выведении его из организма, если процесс описывается формулой

C(t) C e at ,

где	C0	= 2	мг/л, ( C0 - концентрация вещества	при
t =0),		a 0.05	1/c.
32)	Зависимость барометрического давления от			вы-

соты при условии постоянства температуры определяется барометрической формулой

p	p	e kh ,
где	k	- константа, h - высота, p - давление при
h = 0.
	Получить формулу для градиента давления.
	33) Количество электричества, прошедшего че-
рез	проводник, начиная с момента времени		t 0 ,
определяется формулой q 2t 2 3t 1. Вычислить			силу
тока в конце пятой секунды.

Соседние файлы в папке metodichka_Fedorovoi-_matanaliz_diffur

#
09.02.2015315.33 Кб71Т е м а 1.pdf
#
09.02.2015242.03 Кб44Т е м а 2.pdf
#
09.02.2015251.88 Кб52Т е м а 3.pdf
#
09.02.2015254.64 Кб44Т е м а 4.pdf
#
09.02.2015204.3 Кб49Т е м а 5.pdf
#
09.02.2015300.32 Кб52Т е м а 6.pdf