1. Назначение и классификация РТС. Канал связи и радиолокационный канал

Радиотехническая система (РТС) – совокупность устройств, обеспечивающих выполнение конкретных относительно самостоятельных задач с использованием радиосигналов.

Область применения РТС: телевидение, радиолокация, радиоуправление, радионавигация, реализация методов измерения в различных отраслях (биологии, медицине, геологии и др.).

Особенности радиотехнических систем:

1. Целостность – наличие у системы единого функционального назначения. При этом свойства системы нельзя свести к сумме свойств составляющих ее частей.

2. Иерархичность – часть системы может рассматриваться как система более низкого уровня, в свою очередь сама система может быть частью более сложной системы.

3. Сложность – наличие сложных взаимосвязей между различными переменными , описывающими систему.

4. Случайность – влияние на характер функционирования множества внутренних и внешних случайных факторов.

5. Автоматизация – широкое использование в структуре РТС вычислительных средств различного уровня и назначения.

Классификация радиотехнических систем

1. Системы передачи информации – системы связи (многоканальная радиосвязь, радиорелейная связь, связь через искусственные спутники Земли, мобильная радиосвязь), радиовещание и телевидение, телеметрия, передача команд.

2. Системы извлечения информации: осуществляют извлечение информации из сигналов, излученных в направлении на объект и отраженных от него (радиолокация, радионавигация), из сигналов других радиотехнических систем (радиоизмерение, радиоразведка), из собственных радиоизлучений различных объектов (пассивная радиоастрономия).

3. Системы радиоуправления: обеспечивают управление различными объектами или процессами с помощью радиосигналов (радиоуправление ракетами, радиоуправление космическими аппаратами).

4. Системы разрушения информации: служат для создания помех нормальной работе конкурирующей радиосистемы путем излучения мешающего сигнала или путем переизлучения сигнала подавляемой радиосистемы после умышленного искажения.

Канал связи — система технических средств и среда распространения сигналов для односторонней передачи данных (информации) от отправителя (источника) к получателю (приёмнику).

Радиолокационный канал включает в себя: радиолокационную станцию (РЛС), носитель РЛС, среду распространения радиоволн, группу объектов (цели, ориентиры, помехи), систему навигации и систему индикации и управления каналом. Все эти элементы структуры участвуют в процессе обнаружения и определения характеристик заданных объектов.

2. Элементы общей задачи приема. Частные задачи приема

Элементы общей задачи приёма

Задача приёма сигналов состоит в наилучшем воспроизведении информации, заключённой в сигнале искажённом помехами. Оптимизация приёма сводится к следующему. По заранее известным (априорным) некоторым характеристикам передаваемого сигнала, канала и помех, зная их функциональное взаимодействие, необходимо получить оптимальное приёмное или решающее устройство, наилучшим образом воспроизводящее переданное сообщение. Точность и простота решения задачи зависят от объёма априорных сведений.

Элементы общей теории приема сигналов:

1. Событие (event) – e

2. Сигнал (signal) – s

3. Наблюдение – y=n+s (noise)

4. Решение (decision) – d

Частные задачи приема сигналов: обнаружение – установление факта наличия сигнала при приеме. Выдвигаем две гипотезы:

Н₀ – сигнала нет, т.е y=n

H₁ – в шуме есть сигнал, т.е y=n+s

	H0	H1
d0	ПО – правильное необнаружение	ПР – пропуск сигнала
d1	ЛТ – ложная тревога	ПО – правильное обнаружение

M – модель – описание гипотез при помощи формул

K – критерий обнаружения (качество обнаружения)

F=P(d1/H0) – ошибка первого рода (ложная тревога)

D= P(d1/H1) – обнаружение

1) Обнаружение сигнала

В задаче обнаружения сигнала неизвестен сам факт наличия или отсутствия сигнала 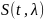, в принятом колебании . Сигнал представляет известную функцию времени и параметров .

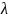Колебаниеr t представляется в виде

где 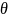- параметр обнаружения, случайная величина, принимающая одно из двух значений: 0 (сигнал отсутствует), 1 (сигнал присутствует).

2) Различение сигналов

В простейшей задаче различения сигналов предполагается наличие в смеси одного из двух сигналов 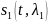или .

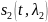3) Оценка параметров сигнала

В задаче оценки параметров сигнала считается, что один из параметров сигнала 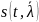, является случайной величиной, априорная плотность вероятности которого известна. Параметр представляет один из компонентов вектора . Задача оценки заключается в определении с минимальной погрешностью значения параметра по принятой на интервале реализации смеси .

4) Фильтрация сообщений

Задача фильтрации сообщений возникает в случае, если сигнал , зависит от некоторого информационного параметра , представляющего случайную функцию времени с известными статистическими характеристиками. На основании статистических характеристик помехи необходимо из принятой смеси выделить наилучшим образом функцию , т.е. получить оценку 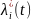реализации информационного параметра.

5) Разрешение сигналов

В простейших задачах разрешения сигналов предполагается, что смесь представляет сумму помехи и двух налагающихся, возможно, сигналов 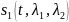и , зависящих, например, от двух параметров :

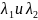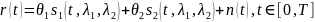
При возможности одновременного наличия в смеси двух сигналов ставится задача их раздельного обнаружения или раздельного обнаружения с оценкой значений параметра 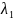в обоих сигналах. Первый сигнал считается разрешённым в смысле обнаружения (оценки параметра ), если показатели обнаружения (оценки параметра ) первого сигнала остаются выше допустимых в присутствии случайного второго сигнала.

3. Основные характеристики одномерной св

Случайная величина — это переменная, значения которой представляют собой исходы какого-нибудь случайного феномена или эксперимента

Дискретная СВ Х : принимает конечное число значений {x_i}, i=1,…,N. Описывается вероятностями: {P_i=P(X=x_i)}, совокупность – закон распределения вероятностей

Непрерывная СВ имеет непрерывную область случайных значений. Описывается функцией распределения F_x(x)=F(x)=P(X<x)

Плотность вероятности:

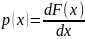
Характеристическая функция – преобразование Фурье от плотности вероятности:

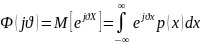
Числовые характеристики – моменты:

Математическое ожидание (начальный момент первого порядка): среднее значение

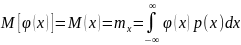
Дисперсия (центральный момент второго порядка): характеризует концентрацию ПВ р(х) в окрестности МО

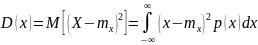
Моментом порядка k случайной величины Х относительно числа b называется математическое ожидание:

Начальным моментом или просто моментом порядка k называют M[x^k]

Центральный момент порядка k - это момент относительно центра распределения 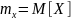, т.е.

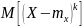
4. Типовые семейства распределений одномерной св

Равномерное

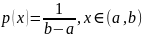
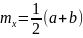
Пример использования: описание случайной фазы сигнала, принимающей значения [-π,π]

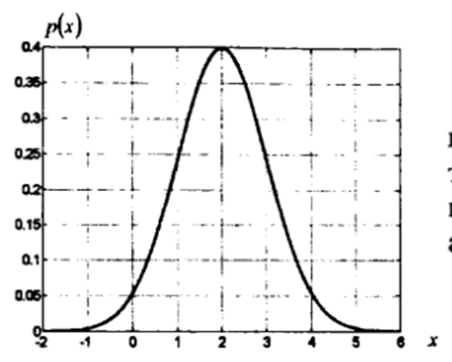
Нормальное (гауссовское):

Пример использования: для описания флуктуационных явлений в аппаратуре

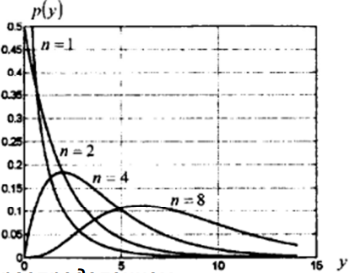
Хи-квадрат распределение: совокупность независимых гауссовских случайных величин, имеющих нулевые МО и одинаковые дисперсии.

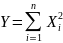
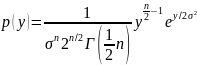
y ≥ 0 , n – степени свободы

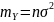
При n=2 – экспоненциальное распределение

В случае, когда величины Хi имеют ненулевые мат ожидания, распределение – нецентральное

Пример: распределение квадрата огибающей радиосигнала

Релеевское: частный случай хи-квадрат распределения 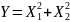. Релеевская СВ: Z=

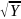
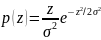
Распределение Райса: обобщение релеевского распределения, когда Хi имеет ненулевые МО.

5. Последовательности св. Виды сходимости

Бесконечная последовательность СВ Xn, n = 1,2, ..., определенная на одном пространстве элементарных событий Ω, называется случайной последовательностью (случайным процессом с дискретным временем) и обозначается

{Xn}, n = 1,2,...

Пусть F_n(x) и F(x) - функции распределения СВ X_n и X соответственно. Случайная последовательность {X_n}, n = 1,2,..., сходится по распределению к СВ X, если последовательность функций распределения F_n(x) СВ X_n сходится к функции распределения F(x) СВ X в каждой точке непрерывности функции F(x), т.е. F_n(x) → F(x) при n → +∞. Этот вид сходимости будем обозначать:

Случайная последовательность {X_n}, n = 1,2,..., сходится почти наверное (п.н.) к СВ X, что записывается 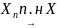, если

Случайная последовательность {X_n}, n = 1,2,..., сходится по вероятности к СВ X, что записывается как: , если если для всех ε > 0 справедливо

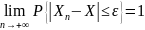
Случайная последовательность {X_n}, n = 1,2,..., сходится к СВ X в среднем квадратическом, что записывается как: 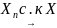, если М[|X_n-X|²]→0 при n→∞

Случайная последовательность {X_n}, n = 1,2,..., является последовательностью независимых СВ X_n, если при любом n СВ X₁,... , X_n независимы.