А. Определение достоверности отличия дисперсии от ожидаемого значения.
Пусть имеются следующие данные:
|
Полученная оценка среднеквадратичного отклонения |
15,9 |
|
Ожидаемая величина среднеквадратичного отклонения |
12 |
|
Число наблюдений N |
35 |
Определим достоверность отличия полученной величины от ожидаемой.
Рассчитаем дисперсии как квадраты среднеквадратичного отклонения:
|
Полученная оценка среднеквадратичного отклонения |
15,9 |
|
Ожидаемая величина среднеквадратичного отклонения |
12 |
|
Число наблюдений N |
35 |
|
Полученная оценка дисперсии |
=В1*В1 |
|
Ожидаемая дисперсия |
=В2*В2 |
Рассчитаем отношение оценки дисперсии к ее ожидаемому значению:
|
Полученная оценка среднеквадратичного отклонения |
15,9 |
|
Ожидаемая величина среднеквадратичного отклонения |
12 |
|
Число наблюдений N |
35 |
|
Полученная оценка дисперсии |
252,81 |
|
Ожидаемая дисперсия |
144 |
|
Отношение оценки и ожидаемого значения |
=В4/В5 |
При истинности проверяемого предположения
полученная величина должна быть
распределена как
.
Умножив отношение наN-1,
получим величину, которая должна быть
распределена как хи-квадрат:
|
Полученная оценка среднеквадратичного отклонения |
15,9 |
|
Ожидаемая величина среднеквадратичного отклонения |
12 |
|
Число наблюдений N |
35 |
|
Полученная оценка дисперсии |
252,81 |
|
Ожидаемая дисперсия |
144 |
|
Отношение оценки и ожидаемого значения |
1,755625 |
|
Полученная величина хи-квадрат |
=В6*(В3-1) |
Рассчитаем вероятность того, что хи-квадрат распределение с данным числом степеней свободы (которое на 1 меньше числа наблюдений) принимает такие или меньшие значения:
Так как мы проверяем гипотезу не о том, что дисперсия меньше ожидаемой, а о равенстве, то рассчитаем и вероятность того, что полученная величина меньше ожидаемой:
|
Полученная оценка среднеквадратичного отклонения |
15,9 |
|
Ожидаемая величина среднеквадратичного отклонения |
12 |
|
Число наблюдений N |
35 |
|
Полученная оценка дисперсии |
252,81 |
|
Ожидаемая дисперсия |
144 |
|
Отношение оценки и ожидаемого значения |
1,755625 |
|
Полученная величина хи-квадрат |
59,69125 |
|
Вероятность того, что хи-квадрат будет больше полученного |
0,00418088 |
|
Вероятность того, что хи-квадрат будет меньше полученного |
=1-В8 |
Теперь доверительная вероятность будет равна минимуму из вероятностей того, что мы получили столько, сколько ожидали, или меньше, и что мы получили столько, сколько ожидали, или больше:
Б. Определение доверительных границ к дисперсии.
Пусть имеются следующие данные:
|
Полученная оценка среднеквадратичного отклонения |
15,9 |
|
Число наблюдений N |
35 |
|
р |
0,05 |
Рассчитаем доверительные границы.
Для начала рассчитаем дисперсию
|
Полученная оценка среднеквадратичного отклонения |
15,9 |
|
Число наблюдений N |
35 |
|
р |
0,05 |
|
Полученная оценка дисперсии |
252,81 |
Так как отношение дисперсии и ее оценки
распределено как
,
то для начала рассчитаем для заданного
р минимальные и максимальные ожидаемые
величины хи-квадрат распределения. Это
можно сделать при помощи функции ХИ2ОБР.
Так как эта функция рассчитывает процентили для заданной вероятности , то, чтобы получить доверительные границы с доверительной вероятностью 1-р нам надо слева и справа «отщипнуть» по р/2, то есть рассчитать процентили с=р/2 и=1-р/2
Так как распределение оценки дисперсии
Sимеет вид
,
то есть если
ожидается в пределах отaдоb, то при заданномSвеличина дисперсииDожидается в пределах от
до
.
Отсюда имеем:
|
Полученная оценка среднеквадратичного отклонения |
15,9 |
|
Число наблюдений N |
35 |
|
р |
0,05 |
|
Полученная оценка дисперсии |
252,81 |
|
Ожидаемое значение хи-квадрат распределения: |
|
|
От |
51,9660216 |
|
До |
19,8062372 |
|
Ожидаемое значение дисперсии: |
|
|
От |
=В4*(В2-1)/В6 |
|
До |
=В4*(В2-1)/В7 |
Взяв квадратный корень из границ для дисперсии, получим доверительные границы для среднеквадратичного отклонения:
|
Полученная оценка среднеквадратичного отклонения |
15,9 |
|
Число наблюдений N |
35 |
|
р |
0,05 |
|
Полученная оценка дисперсии |
252,81 |
|
Ожидаемое значение хи-квадрат распределения: |
|
|
От |
51,9660216 |
|
До |
19,8062372 |
|
Ожидаемое значение дисперсии: |
|
|
От |
165,406928 |
|
До |
433,981474 |
|
Ожидаемое значение среднеквадратичного отклонения |
|
|
От |
=корень(В9) |
|
До |
=корень(В10) |
А там и рассчитать погрешности (понимаемые как расстояния до границ доверительного интервала):
|
Полученная оценка среднеквадратичного отклонения |
15,9 |
|
Число наблюдений N |
35 |
|
р |
0,05 |
|
Полученная оценка дисперсии |
252,81 |
|
Ожидаемое значение хи-квадрат распределения: |
|
|
От |
51,9660216 |
|
До |
19,8062372 |
|
Ожидаемое значение дисперсии: |
|
|
От |
165,406928 |
|
До |
433,981474 |
|
Ожидаемое значение среднеквадратичного отклонения |
|
|
От |
12,8610625 |
|
До |
20,832222 |
|
Погрешность - |
=В1-В12 |
|
Погрешность + |
=В13-В1 |
В результате получим:
|
Полученная оценка среднеквадратичного отклонения |
15,9 |
|
Число наблюдений N |
35 |
|
р |
0,05 |
|
Полученная оценка дисперсии |
252,81 |
|
Ожидаемое значение хи-квадрат распределения: |
|
|
От |
51,9660216 |
|
До |
19,8062372 |
|
Ожидаемое значение дисперсии: |
|
|
От |
165,406928 |
|
До |
433,981474 |
|
Ожидаемое значение среднеквадратичного отклонения |
|
|
От |
12,8610625 |
|
До |
20,832222 |
|
Погрешность - |
3,03893752 |
|
Погрешность + |
4,93222202 |
В. Определение достоверности отличия двух оценок дисперсий.
Воспользуемся данными таблицы PNEVMO. Рассчитаем параметры температуры на момент госпитализации с делением пациентов по исходу, используя командыAnalyze/CompareMeans/Means
В результате получим следующее:
Report
temperature of the patient
|
УМЕР |
Mean |
N |
Std. Deviation |
|
|
,00 |
38,504 |
923 |
,798 |
|
|
1,00 |
38,569 |
108 |
1,233 |
|
|
Total |
38,511 |
1031 |
,854 |
|
Скопируем таблицу в Excelи рассчитаем дисперсию:
|
Report |
|
|
|
|
|
temperature of the patient |
|
|
|
|
|
УМЕР |
Mean |
N |
Std. Deviation |
Дисперсия |
|
0 |
38,50394 |
923 |
0,798284 |
=D4*D4 |
|
1 |
38,56944 |
108 |
1,232766 |
|
|
Total |
38,5108 |
1031 |
0,853647 |
|
Рассчитаем отношение дисперсий. При этом будем брать отношение дисперсии в той группе, где она больше, к меньшей:
|
Report |
|
|
|
|
|
temperature of the patient |
|
|
|
|
|
УМЕР |
Mean |
N |
Std. Deviation |
Дисперсия |
|
0 |
38,50394 |
923 |
0,798284 |
0,637257 |
|
1 |
38,56944 |
108 |
1,232766 |
1,519712 |
|
Total |
38,5108 |
1031 |
0,853647 |
0,728714 |
|
Отношение дисперсий |
=Е5/Е4 |
|
|
|
В
выборочных совокупностях дисперсии
могут существенно отличаться друг от
друга. Пусть мы производим две выборки
объемами
N1
и N2
из одной генеральной совокупности с
известной дисперсией D
и для каждой выборки
вычисляем оценки выборочной дисперсии
SN1-1
и SN2-1.
Поскольку выборочные дисперсии
распределены как величины
,
их отношение будет подчиняться
распределению Фишера-Снедекора
с числом степеней свободы (N1-1,
N2-1).
Иными словами, различие между
выборочными дисперсиями проводится
по критерию Фишера-Снедекора
с числом степеней свободы (N1-1,
N2-1).
Для вычисления достоверности отличия
дисперсий, используя этот критерий,
можно пользоваться затабулированной
функцией, которая называется FРАСП:
В результате получили, что дисперсия в группе умерших достоверно больше, чем у выживших, причем степень достоверности различий очень высока. И это при том, что средняя температура в этих группах практически одинакова.
Для исследования этой связи округлим температуру с шагом в полградуса:
Рассчитаем летальность в зависимости от этой переменной. Используем команды:
Analyze Descriptive Statistics Crosstabs…
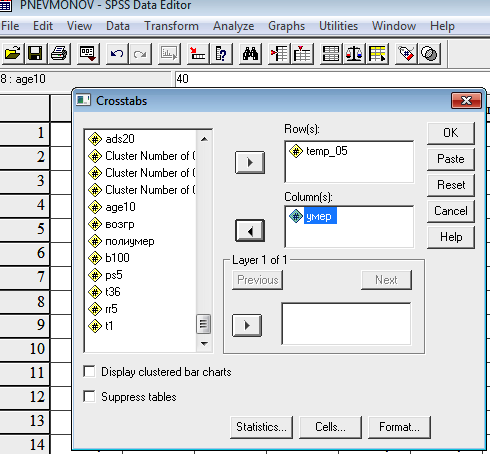
Получаем таблицу:
ТЕМП_05 * УМЕР Crosstabulation
Count
|
|
|
УМЕР |
|
Total |
|
|
|
,00 |
1,00 |
|
|
ТЕМП_05 |
36,00 |
|
3 |
3 |
|
|
36,50 |
|
2 |
2 |
|
|
37,00 |
62 |
16 |
78 |
|
|
37,50 |
89 |
5 |
94 |
|
|
38,00 |
303 |
32 |
335 |
|
|
38,50 |
152 |
3 |
155 |
|
|
39,00 |
197 |
11 |
208 |
|
|
39,50 |
14 |
|
14 |
|
|
40,00 |
104 |
34 |
138 |
|
|
41,00 |
2 |
2 |
4 |
|
Total |
|
923 |
108 |
1031 |
Анализируя полученную таблицу видим, что наибольшая летальность у больных с нормальной, и очень высокой температурой.