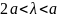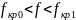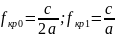- •1. Векторные величины, характеризующие электромагнитное поле (привести все векторные величины, характеризующие поле, их единицы измерения, формулы для их расчета).
- •6. Система уравнений Максвелла с учётом сторонних источников (записать систему уравнений Максвелла со сторонними источниками, пояснить их физический смысл).
- •7. Граничные условия для касательных составляющих векторов электромагнитного поля (записать граничные условия, пояснить их физический смысл, знать из каких уравнений они выводятся и почему).
- •1) При наличии поверхностных токов:
- •2) Отсутствуют поверхностные токи:
- •3) Граничные условия в векторной форме:
- •8. Граничные условия для нормальных составляющих векторов электромагнитного поля (записать граничные условия, пояснить их физический смысл, знать из каких уравнений они выводятся и почему).
- •9. Граничные условия для векторов электромагнитного поля над идеальным проводником (записать граничные условия, пояснить их физический смысл, знать из каких уравнений они выводятся и почему).
- •12. Тангенс угла потерь (что это за величина, ее единица измерения, что данная величина показывает, показать графически и пояснить, что показывают оси действительных и мнимых значений).
- •13. Применение метода зеркальных изображений (суть метода зеркальных изображений, пример его применения, для чего применяется).
- •14. Комплексная диэлектрическая проницаемость (из какого уравнения получается, ее смысл, какие величины в нее входят).
- •15. Элементарные излучатели над полупроводящей поверхностью.
- •20. Средний за период баланс мощностей эм поля.
- •21. Характеристики излучения элементарного электрического диполя.
- •22. Анализ структуры электромагнитного поля элементарного электрического диполя.
- •23. Общие понятия о волновых уравнениях для векторов эм поля.
- •24. Метод решения уравнений Гельмгольца (Электродинамические потенциалы).
- •25. Волновое уравнение для плоской волны и его решение.
- •26. Понятие об излучении электромагнитного поля.
- •27. Понятие о волновом характере электромагнитного поля.
- •28. Линии передачи с поверхностной волной.
- •29. Плоские волны в среде без потерь.
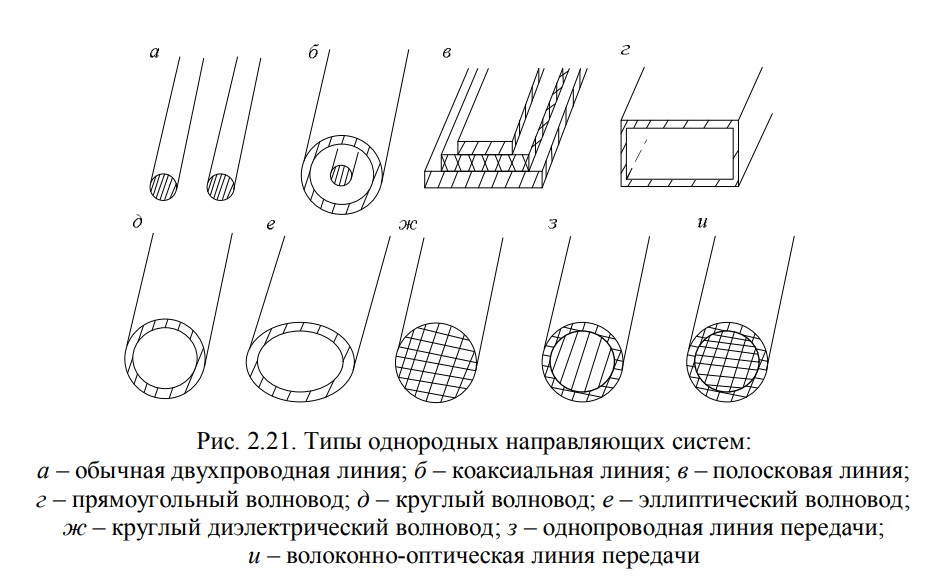
- •30. Классификация направляющих систем, требования к ним.
- •31. Классификация направляемых волн.
- •32. Волноводные линии передачи (прямоугольный волновод)
- •33. Волноводные линии передачи (круглый волновод)
- •34. Плоские волны в средах с потерями.
- •35. Линии передачи с волной tem.
- •36. Ориентация векторов электромагнитного поля.
- •37. Линейная поляризация.
- •38. Условие распространения электромагнитных волн в направляющих системах (критическая длина волны).
- •39. Вращающаяся поляризация.
- •40. Классификация направляемых волн.
- •41. Законы отражения и прохождения на границе раздела двух сред.
- •42. Общие сведения о направляющих системах и направляемых волнах.
- •4 3. Наклонное падение плоской волны при горизонтальной поляризации.
- •44. Наклонное падение плоской волны при вертикальной поляризации.
- •45. Нормальное падение плоской волны.
- •46. Объемные резонаторы.
29. Плоские волны в среде без потерь.




В однородной среде без потерь существует только прямая (бегущая) волна.
В
непоглощающих средах
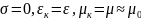
Волновое число вещественное
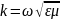
В простейшем случае, векторы ЭМ поля имеют по одной составляющей:
Комплексные амплитуды векторов равны:

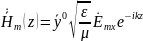
30. Классификация направляющих систем, требования к ним.
Направляющими системами называются устройства, ограничивающие область распространения ЭМВ и направляющие основной поток энергии поля в заданном направлении. Направляющими системами являются все линии передачи электромагнитной энергии, поскольку процесс передачи есть распространение волны. ЭМВ в направляющих системах называют направляемыми.
Направляющие системы служат для передачи энергии ЭМВ, поэтому их еще называют линиями передачи или волноводами
31. Классификация направляемых волн.
По структуре поля ЭМВ в направляющих системах делят на поперечные и продольные. Наличие или отсутствие продольных составляющих векторов и (или) является признаком, по которому классифицируют направляемые волны в направляющих системах. Различают четыре класса направляемых волн:
поперечные, или волны ТЕМ, у которых векторы и перпендикулярны направлению распространения волны, т. е.
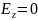 и
и
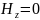 .
По структуре векторы
,
и
идентичны векторам свободно
распространяющихся волн;
.
По структуре векторы
,
и
идентичны векторам свободно
распространяющихся волн;
электрические, или Е-волны, у которых вектор имеет как поперечные, так и продольную
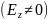 составляющие, вектор
не имеет продольной составляющей
составляющие, вектор
не имеет продольной составляющей
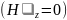 ,
поэтому их называют поперечно-магнитными
волнами или волнами TM;
,
поэтому их называют поперечно-магнитными
волнами или волнами TM;
магнитные, или Н-волны, у которых вектор H имеет как поперечные, так и продольную
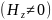 составляющие, а продольная составляющая
вектора
равна нулю
составляющие, а продольная составляющая
вектора
равна нулю
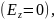 поэтому их называют поперечно-электрическими
волнами или волнами ТЕ;
поэтому их называют поперечно-электрическими
волнами или волнами ТЕ;
гибридные, или смешанные, у которых векторы и наряду с поперечными имеют продольные составляющие
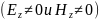 .
Такие волны обозначают
.
Такие волны обозначают
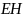 или
или
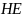 ,
в зависимости от того, какая из продольных
компонент имеет превалирующее значение.
,
в зависимости от того, какая из продольных
компонент имеет превалирующее значение.
Е-,
Н- и гибридные
волны имеют большое многообразие типов
волн, различающихся структурой поля в
поперечном сечении.
Для классификации
этих волн вводят двумерную нумерацию
и обозначают
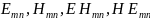 ,
где m и n – целые числа, зависимые от
числа полуволн, укладывающихся вдоль
поперечных размеров направляющей
системы.
,
где m и n – целые числа, зависимые от
числа полуволн, укладывающихся вдоль
поперечных размеров направляющей
системы.
Типы этих волн иногда называют модами.
m – сколько максимумов волны укладывается на широкой стенке; n – сколько максимумов волны укладывается на узкой.
32. Волноводные линии передачи (прямоугольный волновод)
Прямоугольный волновод представляет собой полую металлическую трубу прямоугольного сечения.
Основной тип волны имеет наибольшую критическую длину волны.
В
прям. волноводе могут распространяться
волны типов
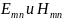 .
.
Для
прямоугольного волновода основной тип
волны является
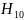 .
.
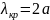
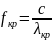
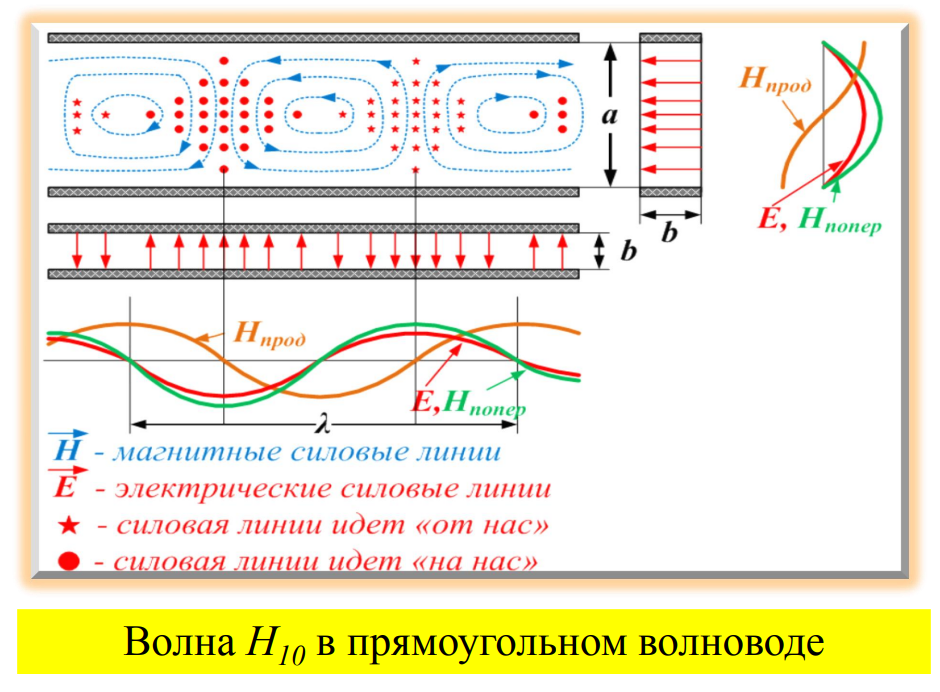
Первым
высшим типом – волна
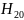 .
.
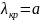
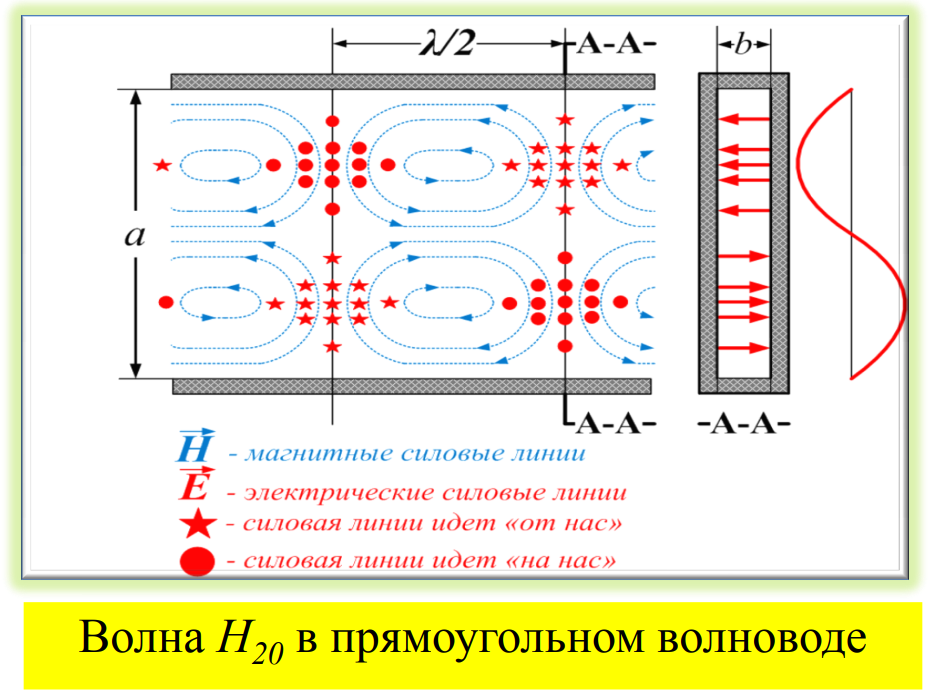
Следовательно, условие одноволнового режима: