
- •1. Векторные величины, характеризующие электромагнитное поле (привести все векторные величины, характеризующие поле, их единицы измерения, формулы для их расчета).
- •6. Система уравнений Максвелла с учётом сторонних источников (записать систему уравнений Максвелла со сторонними источниками, пояснить их физический смысл).
- •7. Граничные условия для касательных составляющих векторов электромагнитного поля (записать граничные условия, пояснить их физический смысл, знать из каких уравнений они выводятся и почему).
- •1) При наличии поверхностных токов:
- •2) Отсутствуют поверхностные токи:
- •3) Граничные условия в векторной форме:
- •8. Граничные условия для нормальных составляющих векторов электромагнитного поля (записать граничные условия, пояснить их физический смысл, знать из каких уравнений они выводятся и почему).
- •9. Граничные условия для векторов электромагнитного поля над идеальным проводником (записать граничные условия, пояснить их физический смысл, знать из каких уравнений они выводятся и почему).
- •12. Тангенс угла потерь (что это за величина, ее единица измерения, что данная величина показывает, показать графически и пояснить, что показывают оси действительных и мнимых значений).
- •13. Применение метода зеркальных изображений (суть метода зеркальных изображений, пример его применения, для чего применяется).
- •14. Комплексная диэлектрическая проницаемость (из какого уравнения получается, ее смысл, какие величины в нее входят).
- •15. Элементарные излучатели над полупроводящей поверхностью.
- •20. Средний за период баланс мощностей эм поля.
- •21. Характеристики излучения элементарного электрического диполя.
- •22. Анализ структуры электромагнитного поля элементарного электрического диполя.
- •23. Общие понятия о волновых уравнениях для векторов эм поля.
- •24. Метод решения уравнений Гельмгольца (Электродинамические потенциалы).
- •25. Волновое уравнение для плоской волны и его решение.
- •26. Понятие об излучении электромагнитного поля.
- •27. Понятие о волновом характере электромагнитного поля.
- •28. Линии передачи с поверхностной волной.
- •29. Плоские волны в среде без потерь.
- •30. Классификация направляющих систем, требования к ним.
- •31. Классификация направляемых волн.
- •32. Волноводные линии передачи (прямоугольный волновод)
- •33. Волноводные линии передачи (круглый волновод)
- •34. Плоские волны в средах с потерями.
- •35. Линии передачи с волной tem.
- •36. Ориентация векторов электромагнитного поля.
- •37. Линейная поляризация.
- •38. Условие распространения электромагнитных волн в направляющих системах (критическая длина волны).
- •39. Вращающаяся поляризация.
- •40. Классификация направляемых волн.
- •41. Законы отражения и прохождения на границе раздела двух сред.
- •42. Общие сведения о направляющих системах и направляемых волнах.
- •4 3. Наклонное падение плоской волны при горизонтальной поляризации.
- •44. Наклонное падение плоской волны при вертикальной поляризации.
- •45. Нормальное падение плоской волны.
- •46. Объемные резонаторы.
9. Граничные условия для векторов электромагнитного поля над идеальным проводником (записать граничные условия, пояснить их физический смысл, знать из каких уравнений они выводятся и почему).
Если
вторая среда является идеальным
проводником
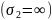 ,
где отсутствует ЭМП, то граничные
условия принимают вид
,
где отсутствует ЭМП, то граничные
условия принимают вид
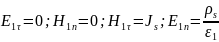
В векторной форме:
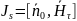
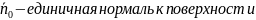
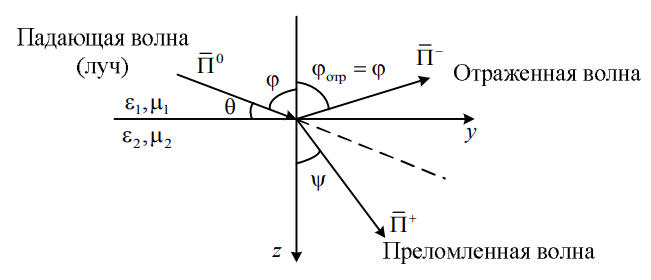
10. Лучевая концепция распространения электромагнитных волн (вспомнить о законах отражения и преломления, записать их, пояснить как в них проявляется лучевая концепция распространения радиоволн, привести еще примеры применения лучевой концепции распространения радиоволн, когда вообще с точки зрения науки корректно ее применение).
Волна
в однородной
изотропной среде
представляется в виде прямолинейного
луча, совпадающего с направлением
распространения волны (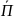 ).
).
Пусть
линейно
поляризованная плоская волна
в виде луча падает на плоскую бесконечно
протяженную границу раздела двух сред
с параметрами
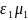 и
и
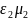 .
.
Угол
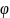 между направлением распространения
между направлением распространения
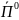 и нормалью (ось z) к поверхности раздела
называют углом падения, при этом угол
скольжения
и нормалью (ось z) к поверхности раздела
называют углом падения, при этом угол
скольжения
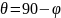 .
.
Угол
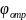 определяет направление отражённой
волны
определяет направление отражённой
волны
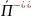 ,
а угол
,
а угол
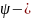 направление преломленной волны
направление преломленной волны
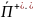
В изотропных средах отраженная и преломленная волны лежат в одной плоскости и удовлетворяют законам отражения и преломления (законам Снеллиуса) следующим образом: угол падения равен углу отражения, т. е.
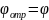
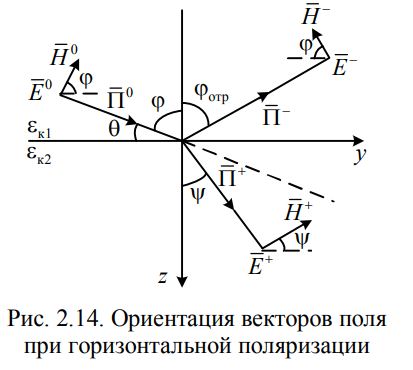
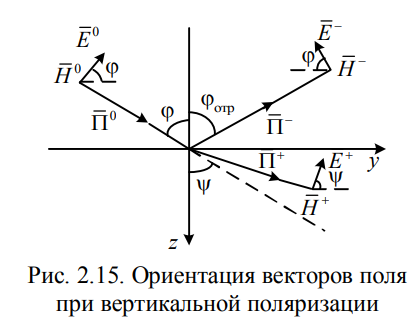
11. Метод комплексных амплитуд (в чем смысл метода, чем он удобен в электродинамике, привести пример использования данного метода, записать комплексную амплитуду, комплексный вектор, гармонический вектор и связь между ними).
На основании формулы Эйлера гармонический вектор линейных операторов определяется как:
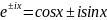
Гармонический вектор
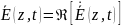

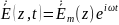
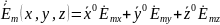
Комплексный вектор в общем случае имеет шесть составляющих с реальной и мнимой частями, каждая из которых имеет по три составляющие на соответствующие координатные оси.
Таким образом, гармонический вектор является частным случаем комплексного вектора и определяется:
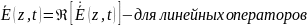
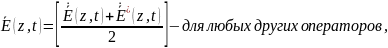
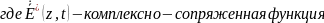
12. Тангенс угла потерь (что это за величина, ее единица измерения, что данная величина показывает, показать графически и пояснить, что показывают оси действительных и мнимых значений).
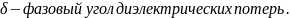
Он определяется как отношение мнимой к вещественной частей комплексного числа.
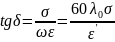
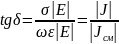
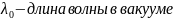
Следовательно,
тангенс угла потерь равен отношению
амплитуды плотности тока проводимости
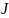 к амплитуде плотности тока смещения
к амплитуде плотности тока смещения
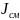 в данной точке пространства.
в данной точке пространства.
Е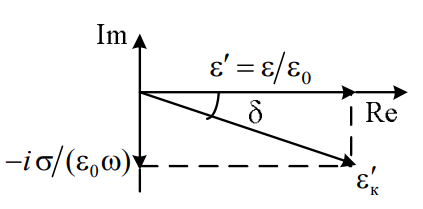 сли
сли
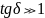 ,
то среда является проводником, а если
,
то среда является проводником, а если
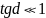 ,
то среда приближается к диэлектрику
без потерь. Принято считать среду
полупроводящей в пределах
,
то среда приближается к диэлектрику
без потерь. Принято считать среду
полупроводящей в пределах
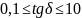
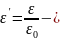 относительная
диэлектрическая проницаемость вещества
или среды
относительная
диэлектрическая проницаемость вещества
или среды
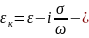 комплексная
диэлектрическая проницаемость среды,
характеризующая свойства среды в
зависимости от круговой частоты
комплексная
диэлектрическая проницаемость среды,
характеризующая свойства среды в
зависимости от круговой частоты
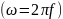
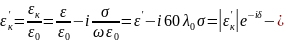 относительная
комплексная диэлектрическая проницаемость
среды
относительная
комплексная диэлектрическая проницаемость
среды
