экзамен 1 курс 2 семестр по билетам / теория матан

БИЛЕТ №1

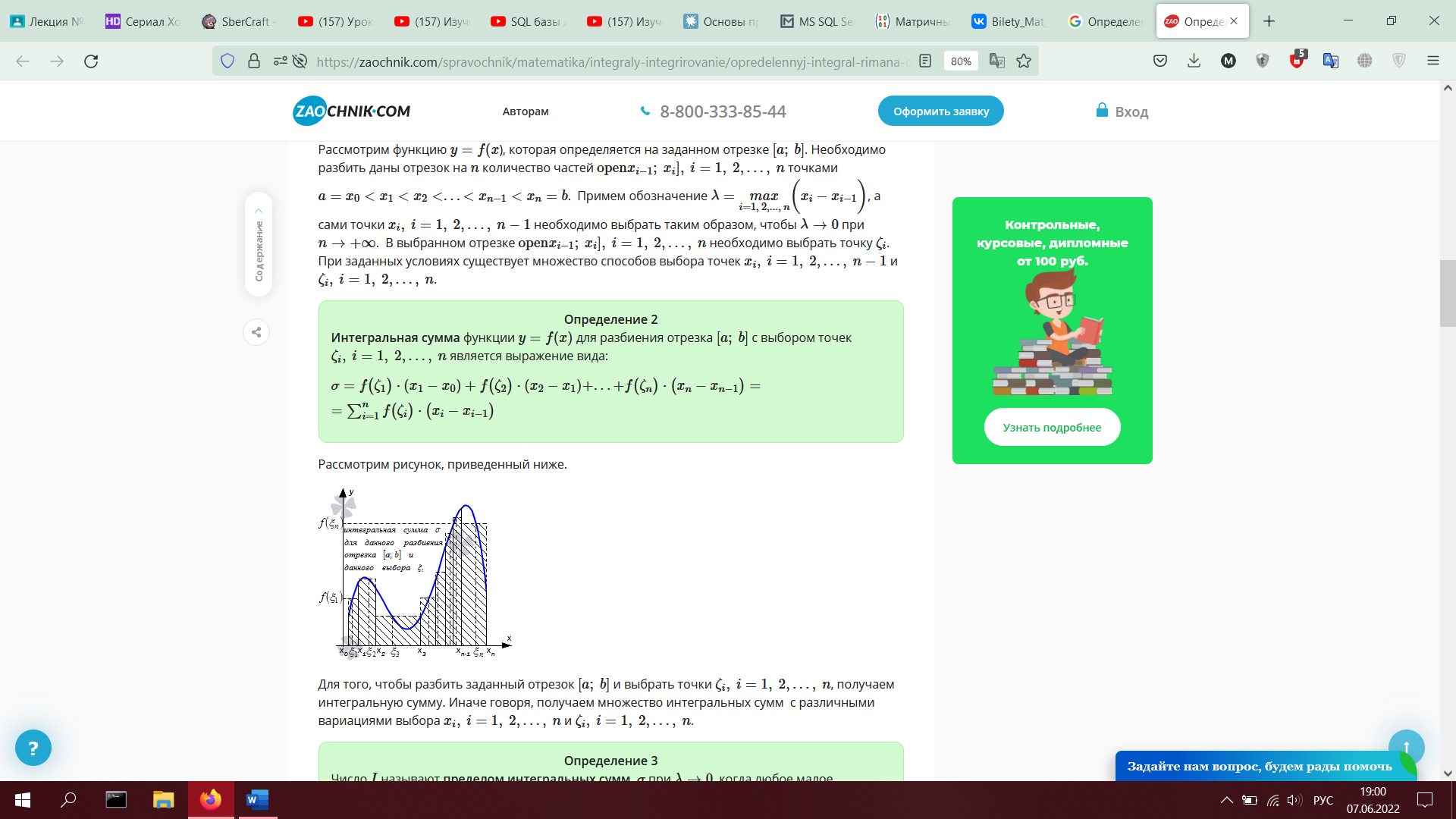
1. Определенный интеграл Римана. Основные определения. Верхняя и нижняя суммы. Свойства сумм Дарбу. Условие интегрируемости

2. Необходимое условие сходимости числового ряда.

БИЛЕТ №2

1 . Классы интегрируемых функций. Свойства интегрируемых функций

2. Формула Тейлора для функций многих переменных.

БИЛЕТ №3

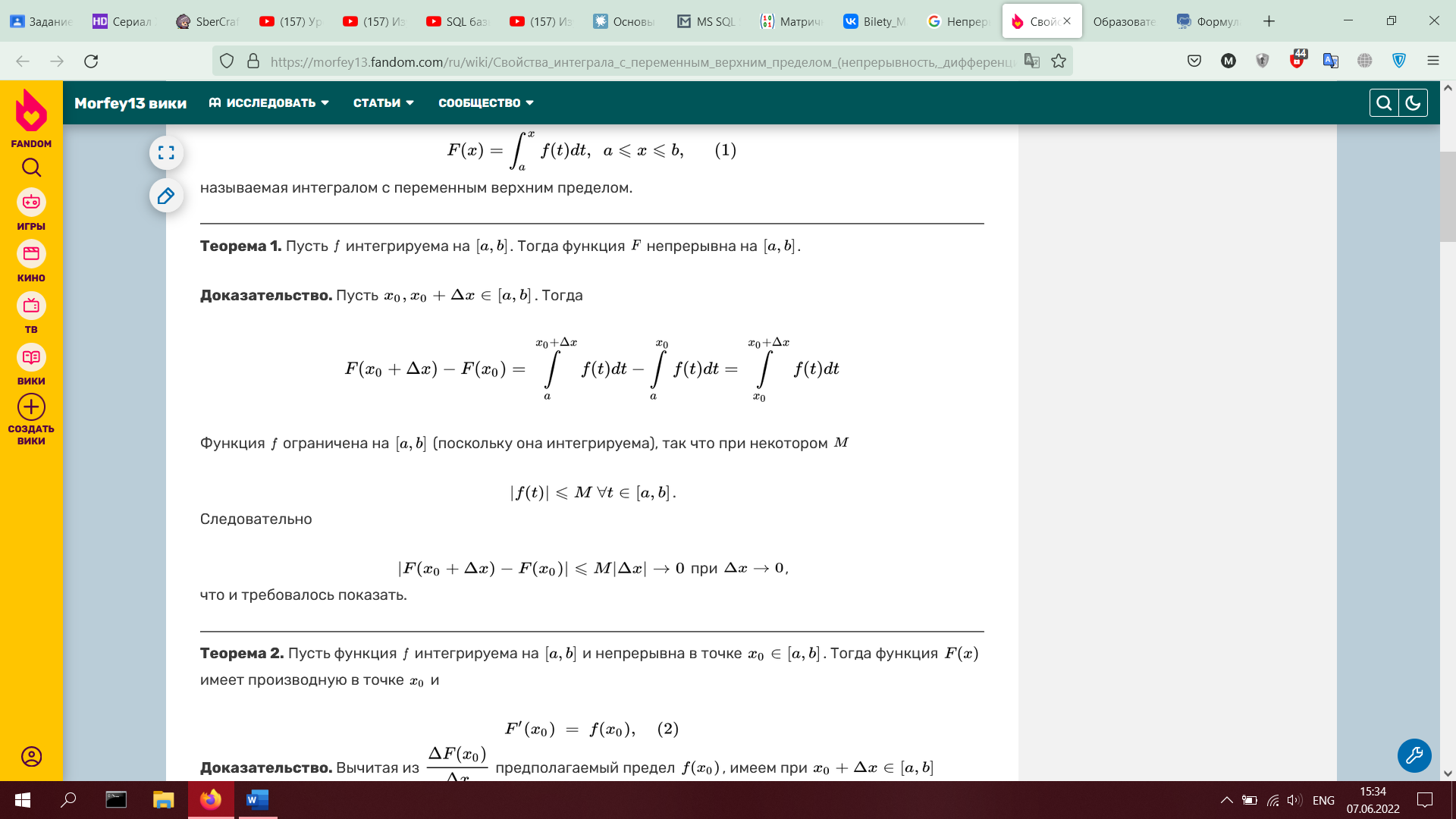
1 . Непрерывность и дифференцируемость интеграла по верхнему пределу.

2. Свойства сходящихся числовых рядов

1. Если ряд сходится, то сходится любой из его остатков. Наоборот, из сходимости какого-то остатка вытекает сходимость всего ряда. Отсюда следует, что изменение или выбрасывание конечного числа членов ряда не изменяет его сходимости или расходимости.

Б ИЛЕТ №4

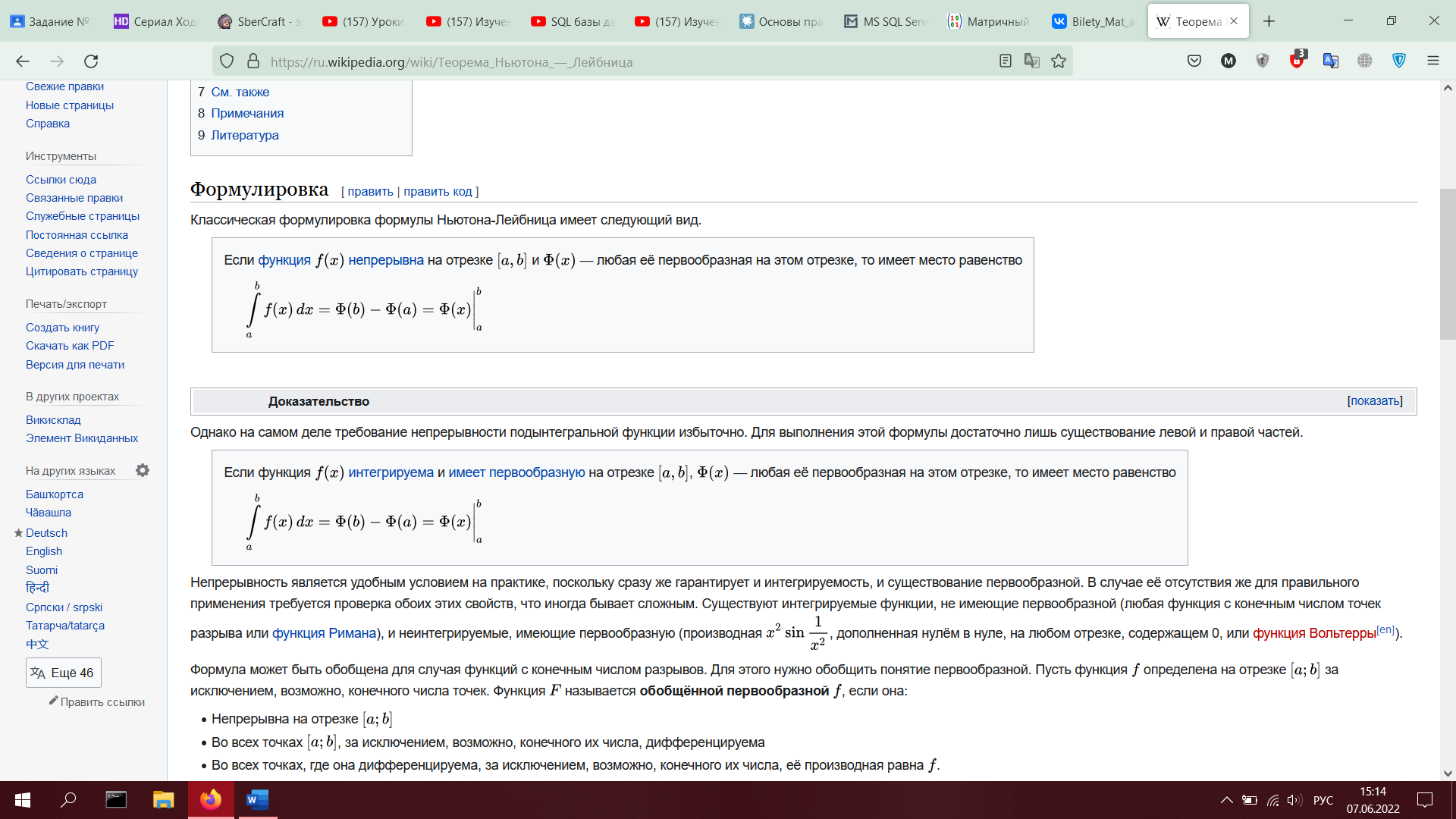
1. Теорема (формула) Ньютона-Лейбница

2. Необходимые условия локального экстремума функции многих переменных

БИЛЕТ №5

1. Замена переменного в определенном интеграле.

2. Условный экстремум. Прямой метод и метод Лагранжа

БИЛЕТ №6

1. Геометрические приложения определенного интеграла.

БИЛЕТ №7

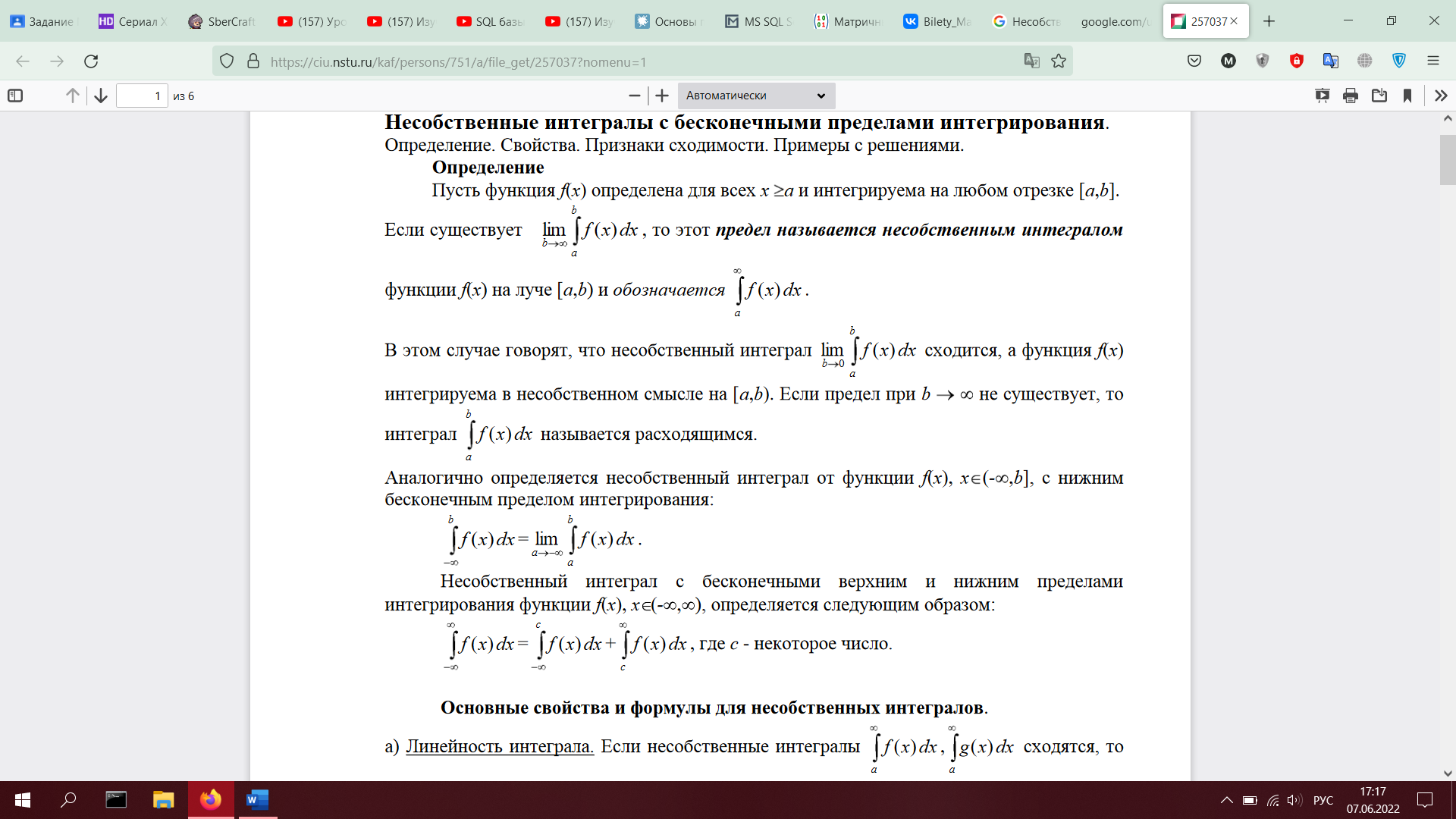
1. Несобственные интегралы с бесконечными пределами. Определения, признаки сходимости.

2. Теорема Вейерштрасса равномерной сходимости функционального ряда.

Б ИЛЕТ №8

1. Несобственные интегралы от неограниченных функций. Определения, признаки сходимости

2. Признак Даламбера сходимости числового ряда.

БИЛЕТ №9

1. Функции нескольких переменных. Предел функции, предел функции по направлению. Примеры.

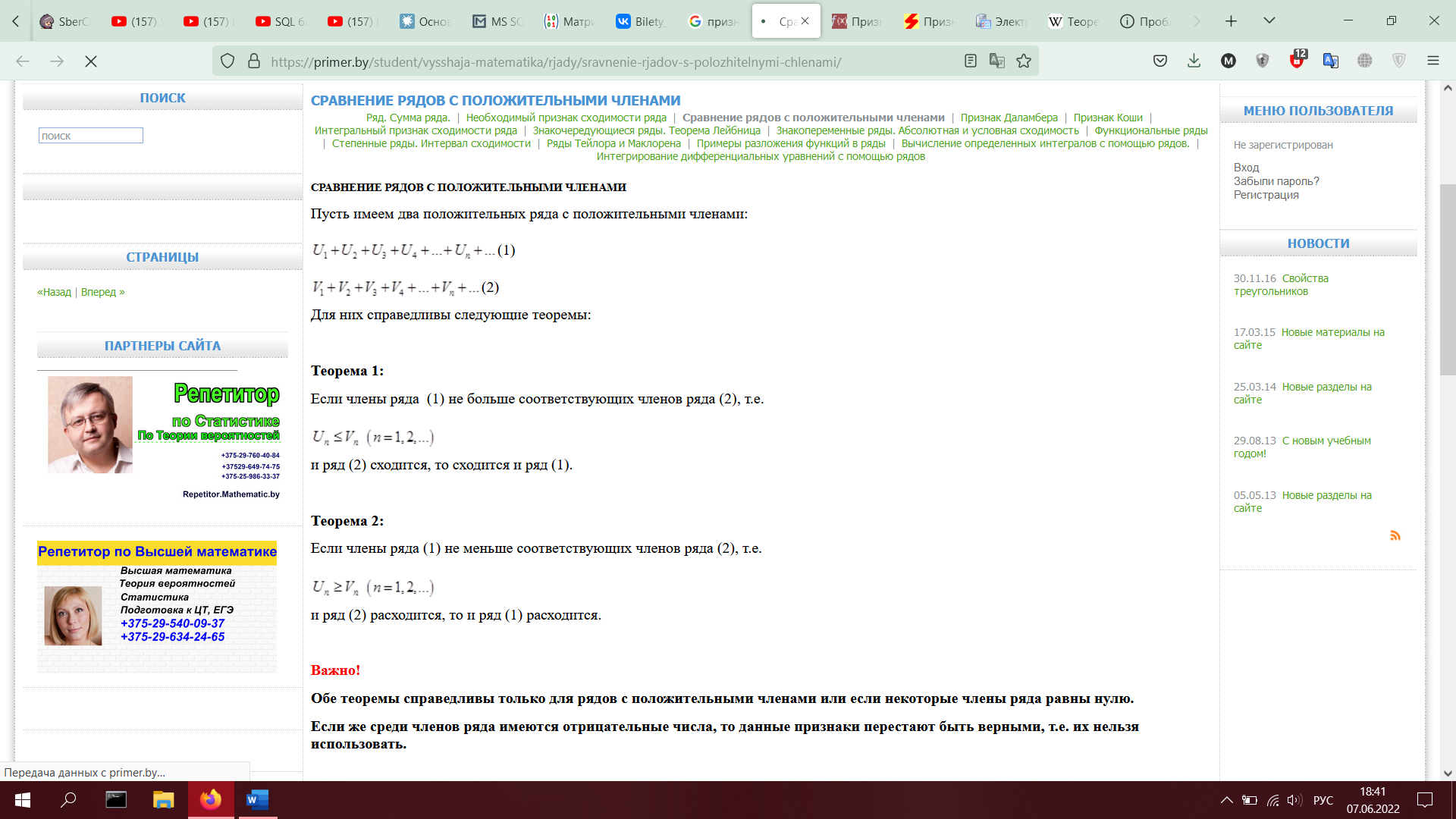
2. Признак сравнения для сходимости числовых рядов с неотрицательными членами, следствие.

БИЛЕТ №10

1. Непрерывность функции нескольких переменных. Свойства

2. Интегральный признак сходимости числовых рядов с неотрицательными членами

БИЛЕТ №11

1. Частные производные, дифференцируемость, дифференциал функции нескольких переменных. Основные определения.

2. Знакопеременные ряды. Признак Лейбница.

БИЛЕТ №12

1. Теорема о дифференцируемости функции нескольких переменных в точке, имеющей частные производные ( НЕ НАШЕЛ)

2. Равномерная сходимость функций и рядов. Признак Вейерштрасса.

БИЛЕТ №13

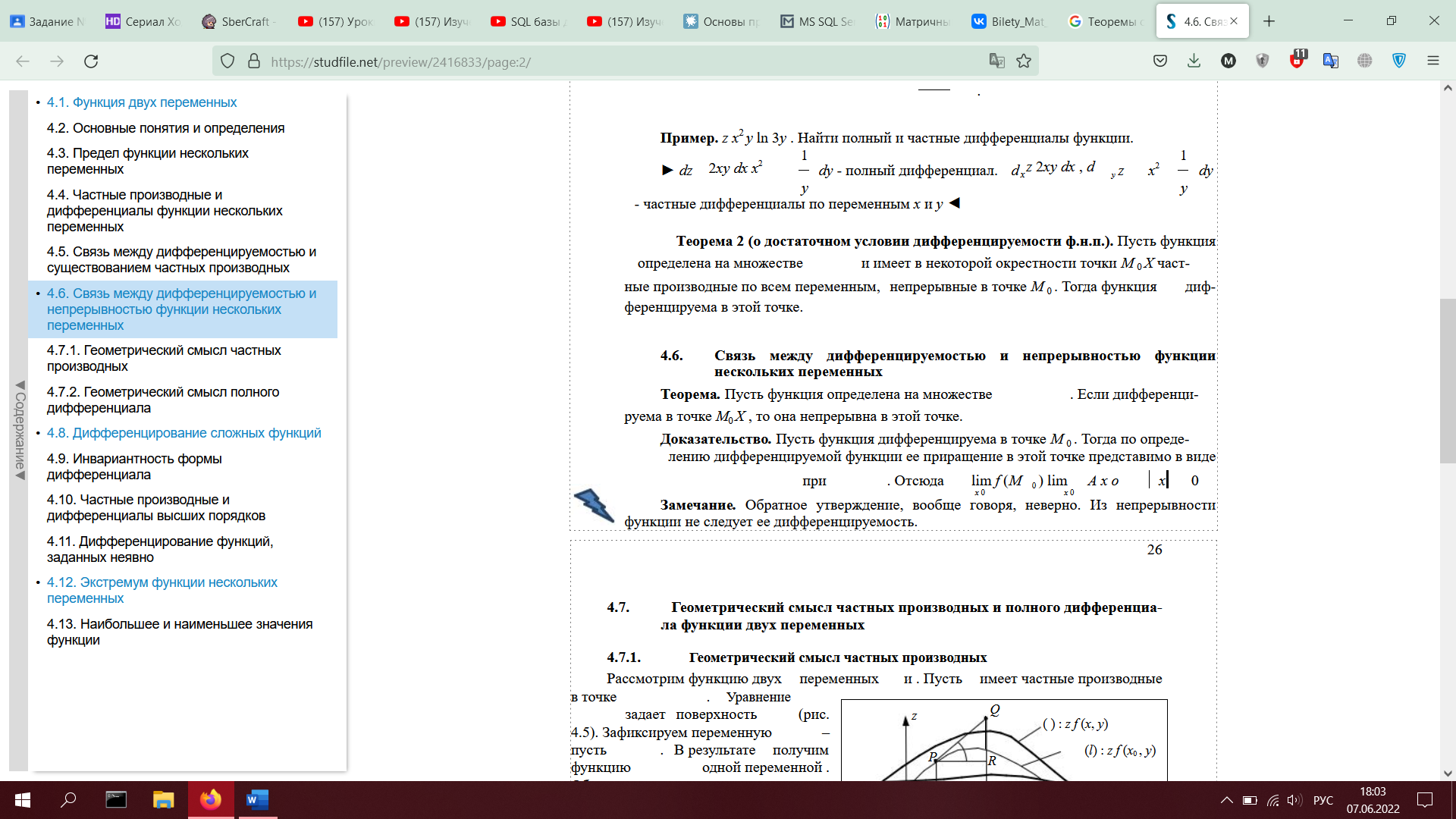
1. Теоремы о связи непрерывности, частных производных и дифференцируемости функций нескольких переменных (!!!! ВОЗМОЖНО НЕПРАВИЛЬНО!!!)

2. Степенные ряды. Радиус сходимости и круг сходимости. Основная теорема (формула Коши -Адамара.

БИЛЕТ №14

1. Частные производные от сложной функции. Теорема о дифференцировании сложной функции.

2. Ряды Тейлора, теорема о разложимости, степенные ряды элементарных функций.

БИЛЕТ №15

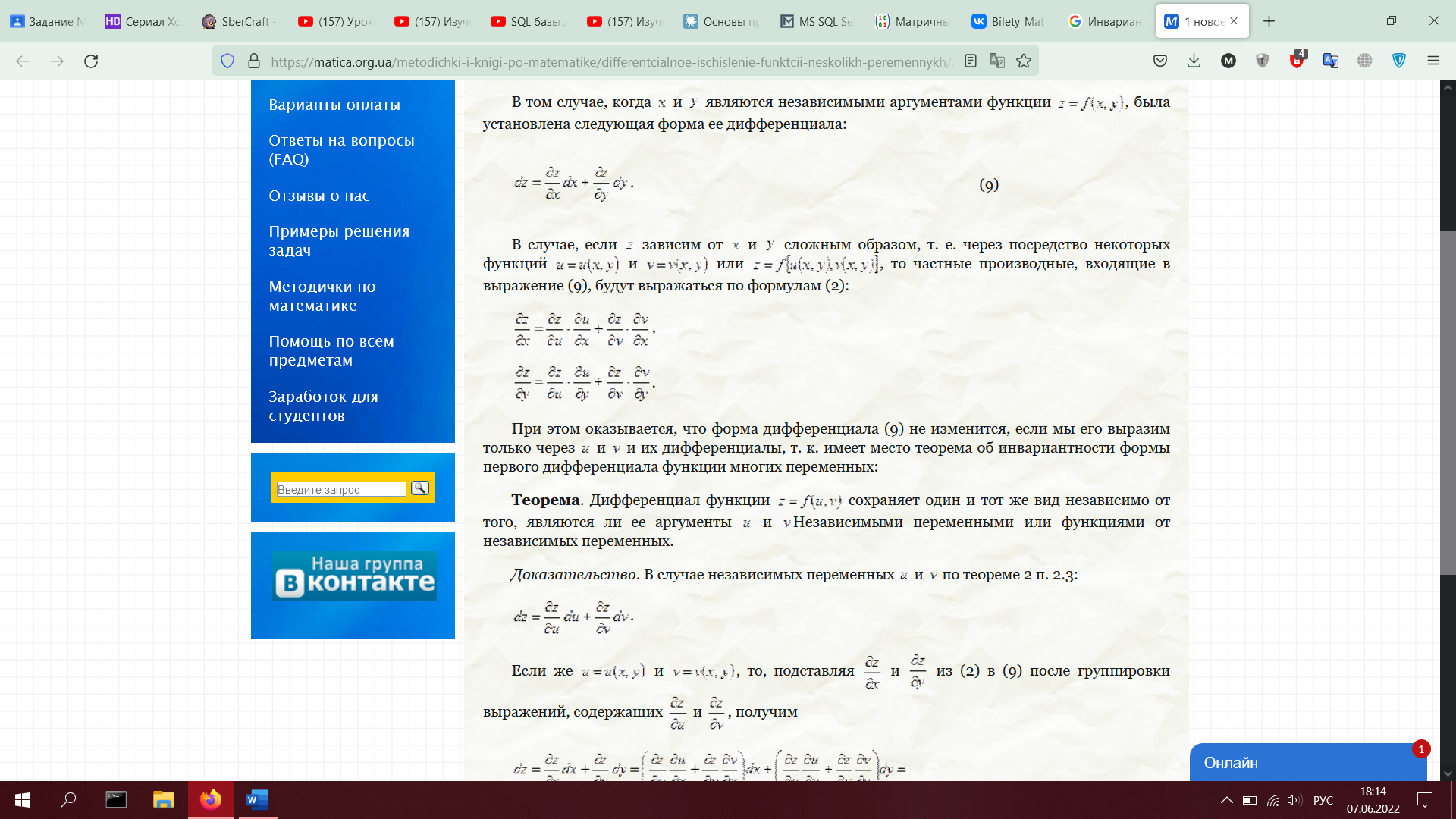
1. Инвариантность формы первого дифференциала функции многих переменных

2. Формула Даламбера для вычисления радиуса сходимости степенного ряда.

БИЛЕТ №16

1. Геометрический смысл частных производных и дифференциала.

2. Почленная дифференцируемость и интегрируемость степенных рядов. Примеры.

БИЛЕТ №17

1. Градиент, производная по направлению ( Другой ответ в Билете №23)

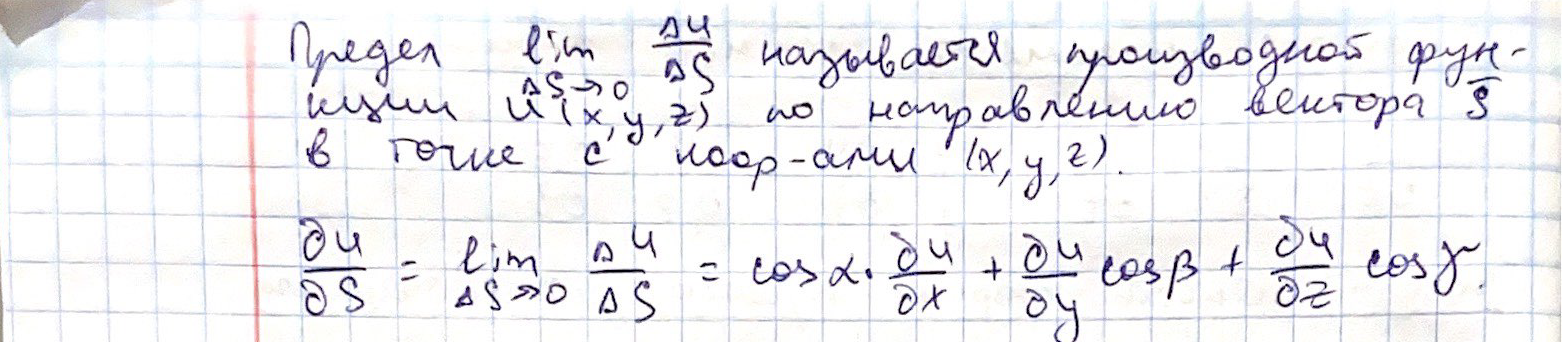
2 Ряды Фурье. Теорема о замкнутости тригонометрической системы и ее следствия.

БИЛЕТ №18

1. Частные производные высших порядков. Теорема о независимости порядка переменных, по которым берется производная

2. Признак Даламбера сходимости числового ряда.

БИЛЕТ №19

1. Дифференциалы высших порядков. Представление с помощью формального символа. Теорема Тейлора (без доказательства).

2. Признаки сравнения для сходимости числовых рядов с неотрицательными членами, следствие.

БИЛЕТ №20

1. Теорема о существовании и дифференцируемости неявно заданной функции нескольких переменных. Дифференцирование неявно заданной функции.

2. Оценки интегралов. Формулы среднего значения.

БИЛЕТ №21

1. Определенный интеграл Римана. Основные определения. Верхняя и нижняя суммы. Свойства сумм Дарбу. Условие интегрируемости

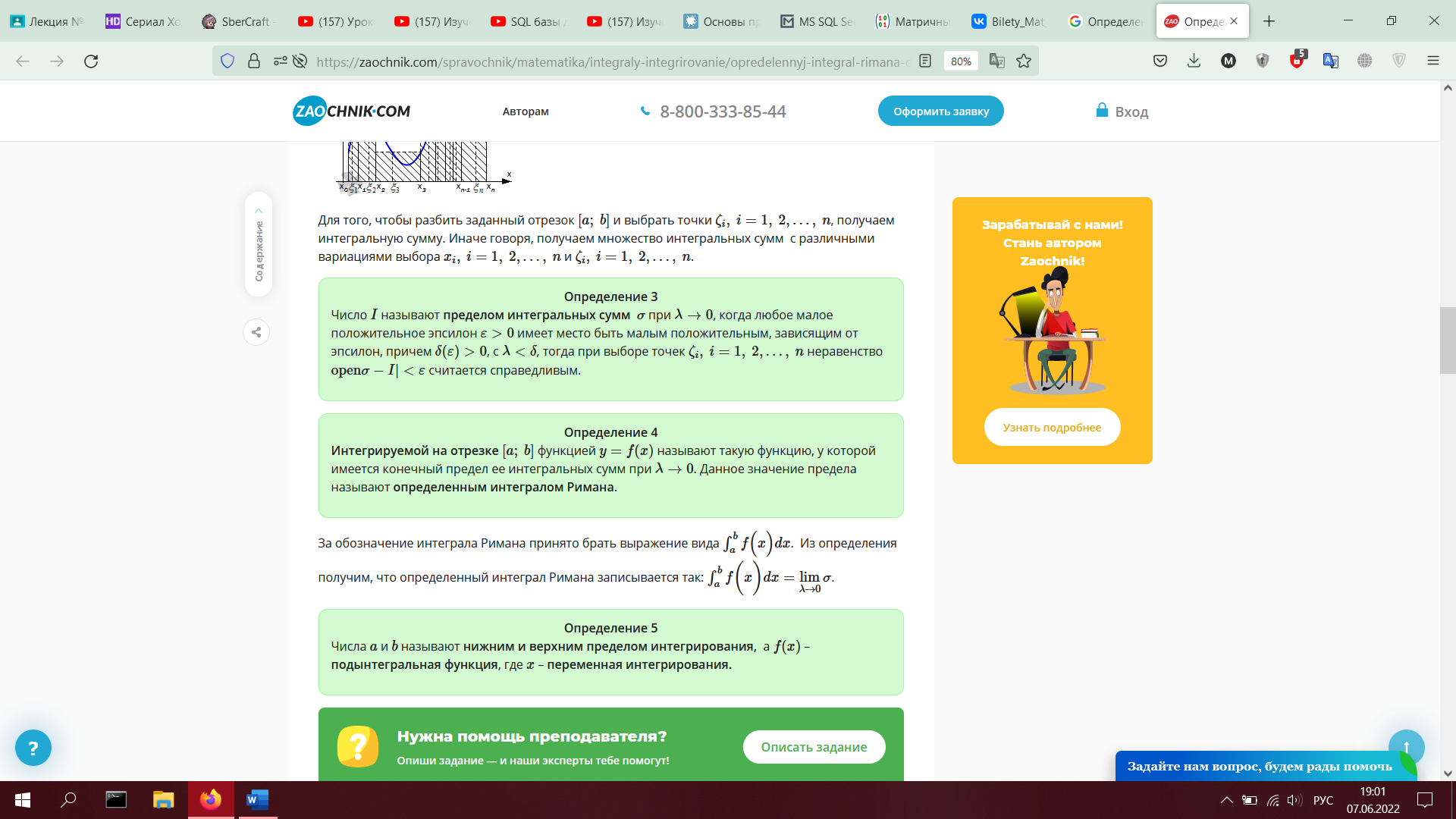
2. Критерий Коши сходимости ряда. Необходимое условие сходимости числового ряда

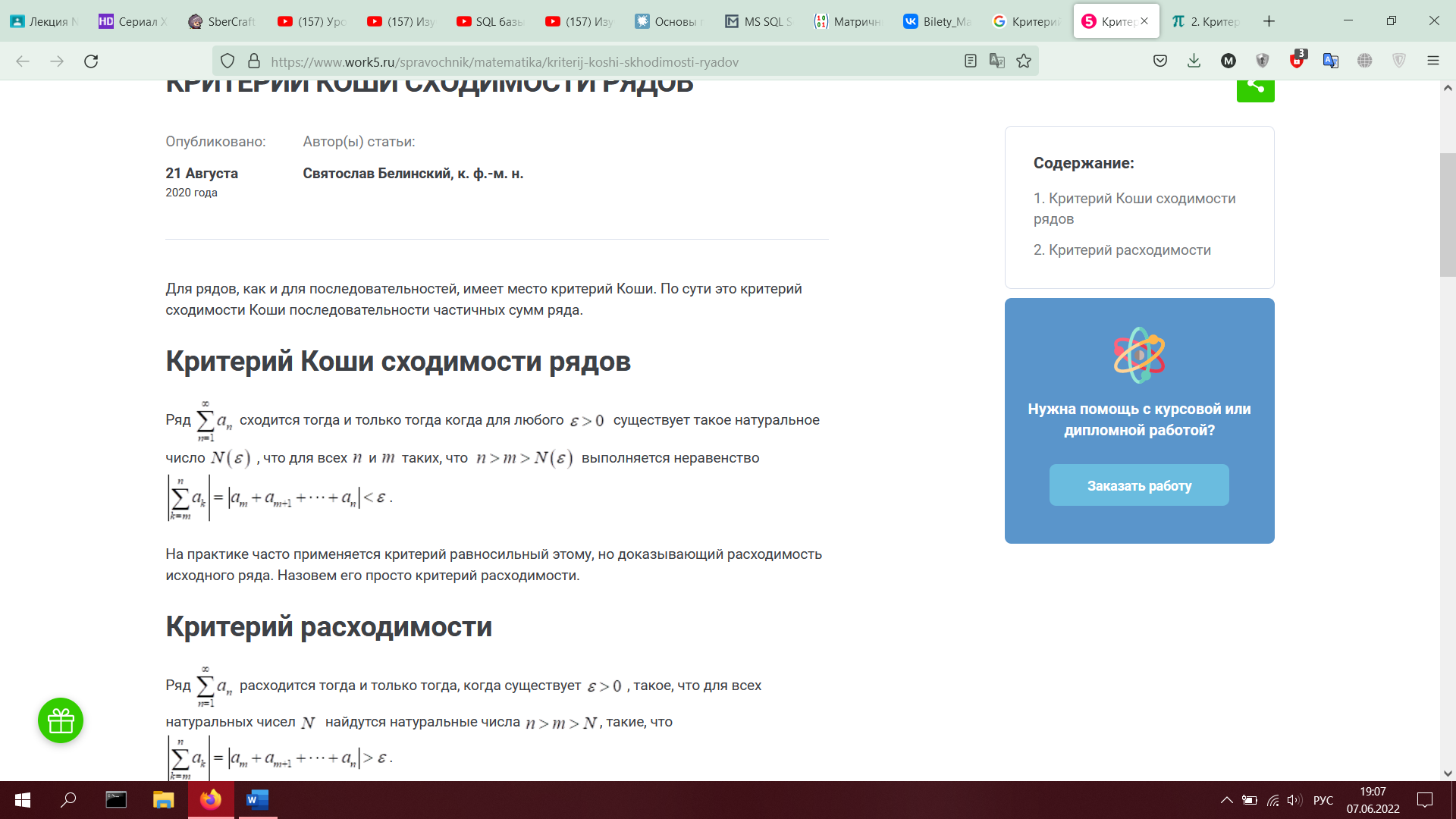
Билет №22

1. Теорема о существовании первообразной непрерывной функции. Формула Ньютона-Лейбница.

2. Неявные функции, определяемые системой функциональных уравнений. Определитель Якоби. Теорема о существовании непрерывно дифференцируемых решений системы функциональных уравнений ( без доказательства)

Билет №23

1. Градиент, производная по направлению

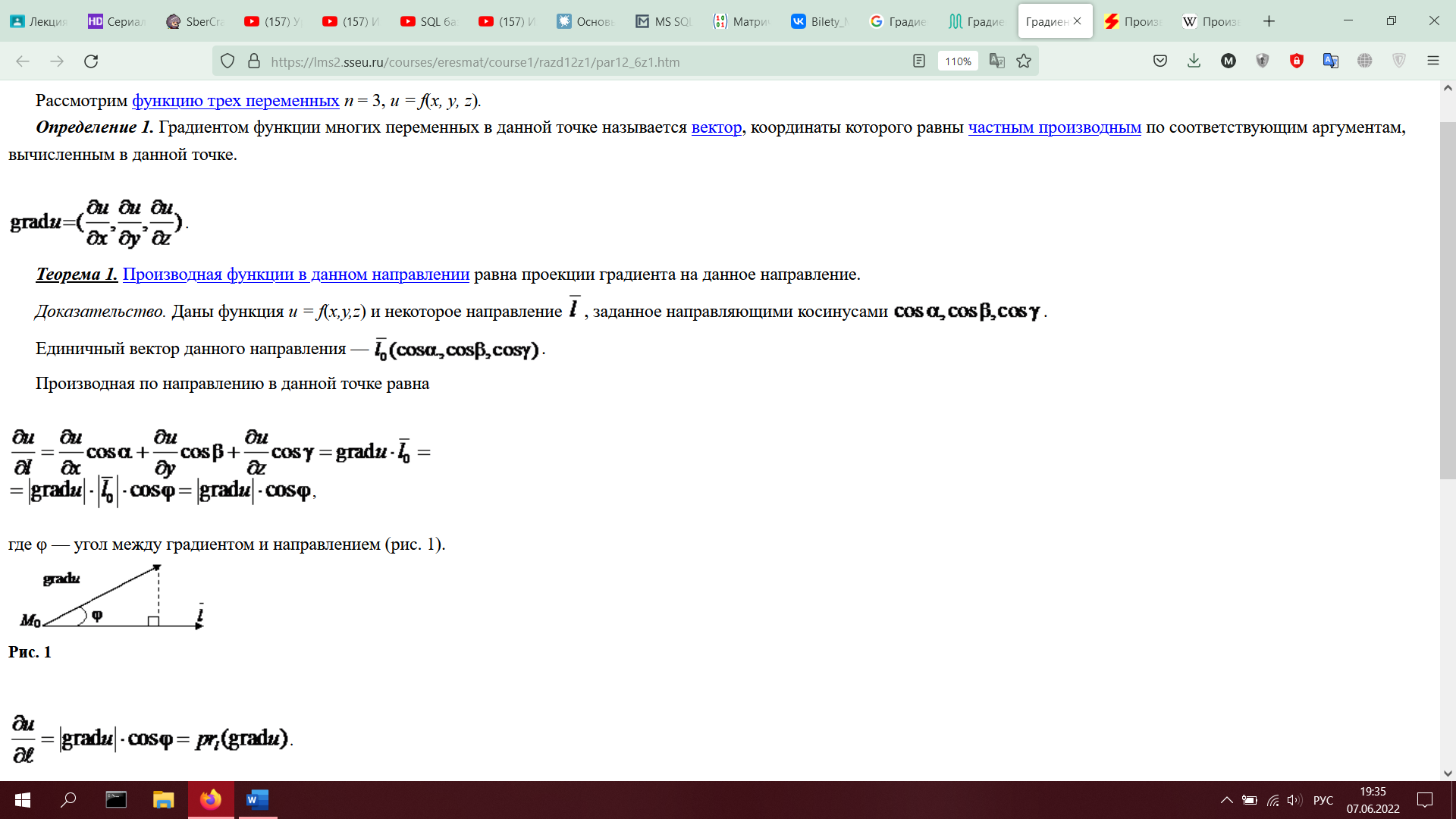
производная по направлению — одно из обобщений понятия производной на случай функции нескольких переменных. Производная по направлению показывает, как быстро значение функции изменяется при движении в данном направлении.

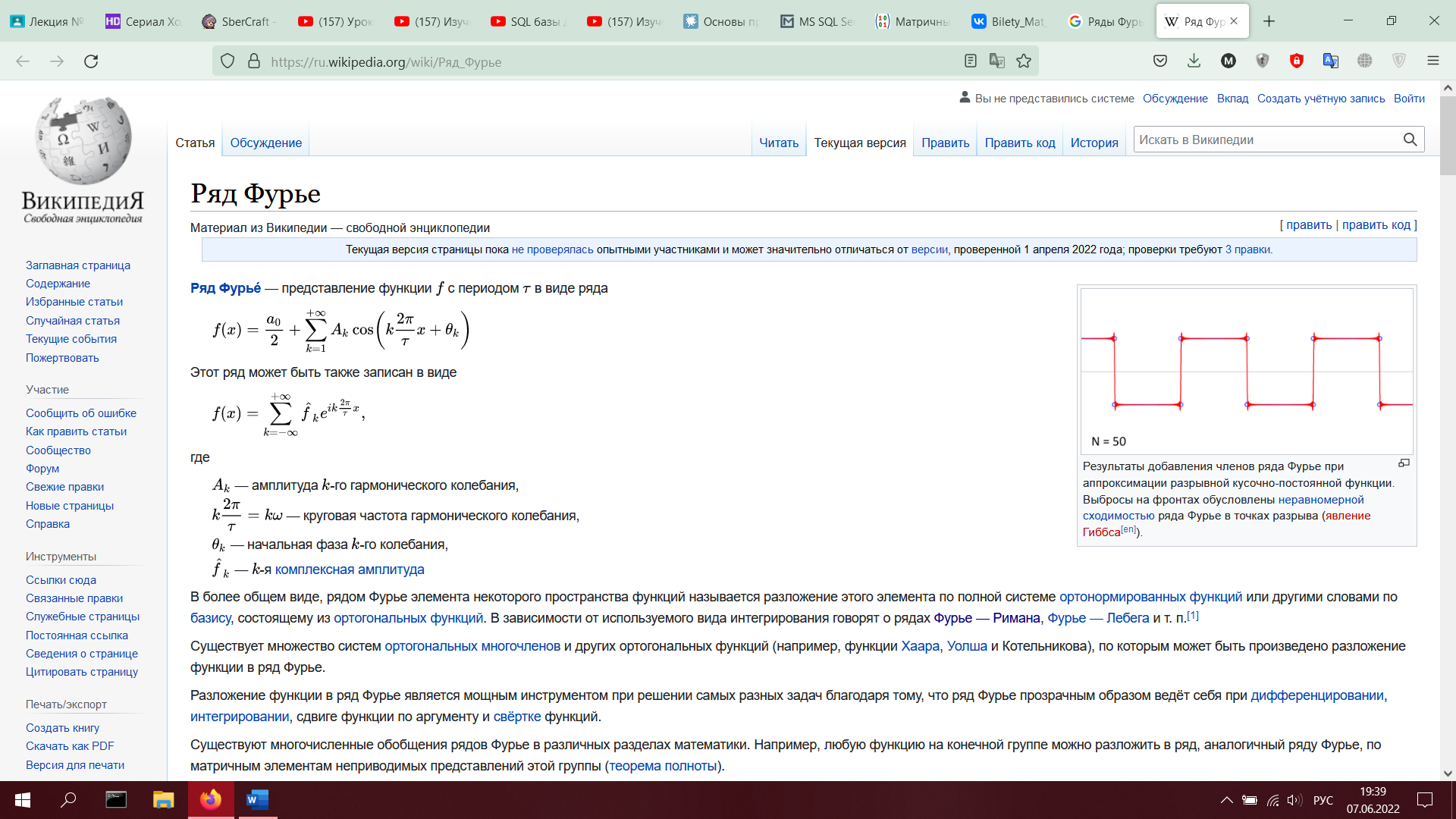
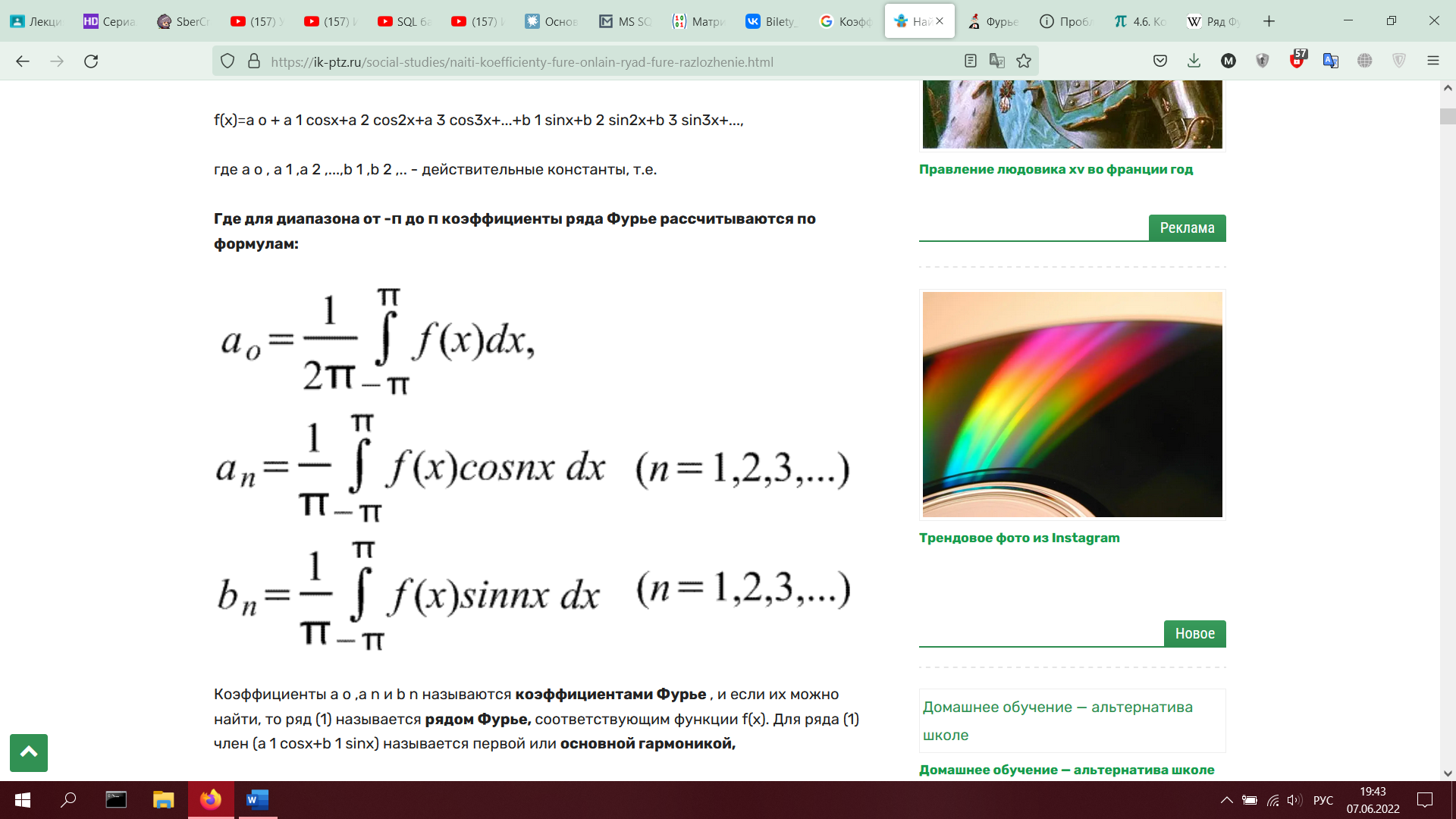
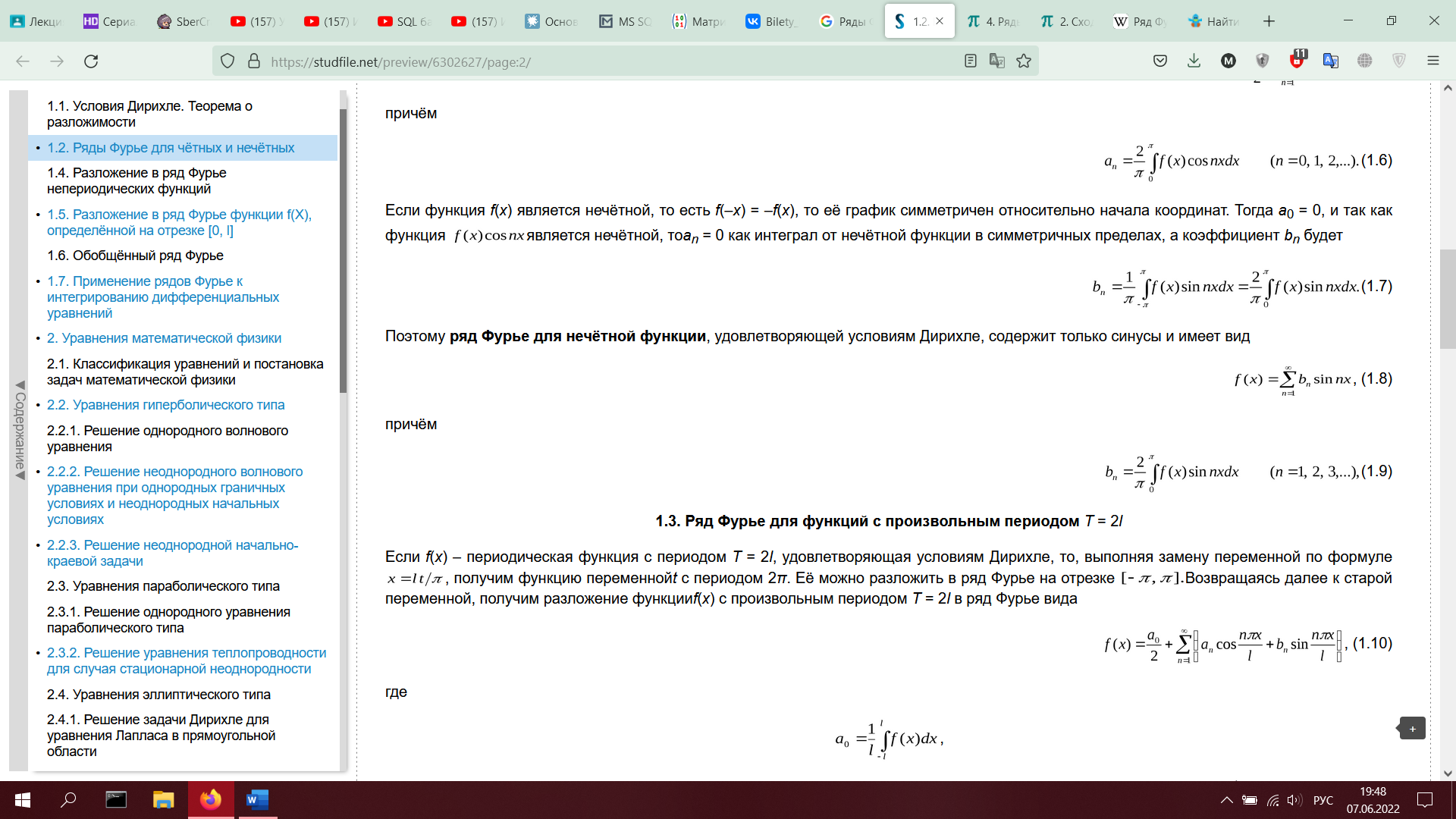
2. Ряды Фурье. Коэффициенты Фурье. Теорема разложимости для кусочно-гладких функций (без доказательства). Ряды Фурье для четных и нечетных функций.)

ЕБАНЫЙ МАТ АНАЛИЗ . ЗАЧЕМ ЕГО ПРИДУМАЛИ ….