
РГР / РГР2 Глазунова П-25
.docxРОССИЙСКИЙ ХИМИКО-ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
имени Д.И. Менделеева
__________________________________________________________________
Кафедра инженерного проектирования технологического оборудования
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №2
РАСЧЕТ ВАЛА С МЕШАЛКОЙ
ВАРИАНТ №364
Студентка группы
Преподаватель доцент Щербак Н.Б.
«__» _____________ 2021 г.
Москва, 2021 г.
РГР 2 Расчет вала с мешалкой
I. Определим перемещение на конце балки (т. К) в заделке (т. А) Δк
1. Строим грузовую эпюру Мp – произвольная
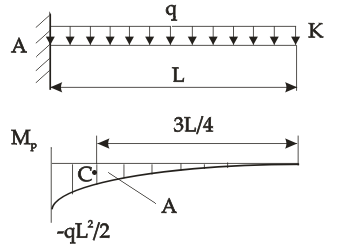
2. Строим вспомогательную систему (ВС) для определения перемещения в точке К в т. К прикладываем единичную силу
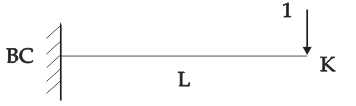
3. Строим единичную эпюру М1 – линейная
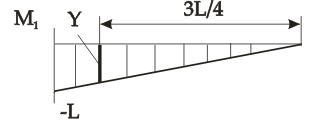
4. Определим перемещение Δк
Δк = ∫(Мp М1)/(ЕIx) = (A Y)/(ЕIx)
Е – модуль упругости первого рода (Юнга)
Ix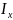 – осевой момент инерции сечения
– осевой момент инерции сечения
Площадь произвольной эпюры А = - (1/3)L(qL2/2) = - (1/6)qL3
Значение линейной эпюры Y, взятая под центром тяжести (3L/4) произвольной эпюры
Y = - 1 (3L/4) = - 3L/4
Тогда
Δк = (A Y)/(ЕIx) = + (1/8) qL4/(ЕIx)
Максимальный изгибающий момент на грузовой эпюре
Мpmax = max|Мp| = qL2/2
Длина лопасти мешалки L
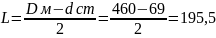
II. 1. Определим интенсивность равномерно распределенной нагрузки q1 из условия прочности при изгибе
σ = Мpmax/Wx ≤ [σ]
где Мpmax = q1L2/2, момент сопротивления при изгибе Wx = bs2/6,
[σ] – допускаемое напряжение при изгибе, тогда
q1L2
6/(2
bs2)
≤
[σ]
и q1
≤
[σ]
bs2/(3
L2)=
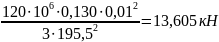
2. Определим интенсивность равномерно распределенной нагрузки q2 из условия жесткости при изгибе
Δк ≤ [dY]л - допускаемый прогиб лопасти мешалки
Ix = bs3/12, Δк = (1/8) qL4/(ЕIx) = (1/8) q2L4 12/(Еbs3) ≤ [dY]л
q2
≤
(2/3)[dY]л
Еbs3/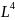 =
=
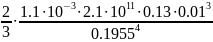 =13,705 кН
=13,705 кН
3. Выбираем из двух значений интенсивности минимальное
q=min
(q1
,
q2)
=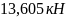
III. Определим крутящий момент Mкр
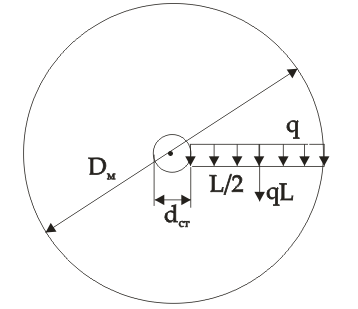
1.Крутящий момент на одну лопасть M1=qL(L+dст)/2
M1=
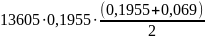 = 0,352
кН·м
= 0,352
кН·м
2.Суммарный крутящий момент Mкр = Z qL(L + dст)/2
где Z – число лопастей.
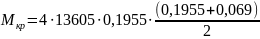 =1,407
кН·м
=1,407
кН·м
3. Определим силы, действующие на колесе
Mкр = Pt Dк/2
Касательная
сила
Pt
= 2Mкр/Dк
=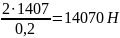
Радиальная
сила Pr
= 0.4
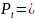
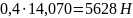
IV. Построим эпюру крутящего момента Mкр
Вариант А Колесо между опорами
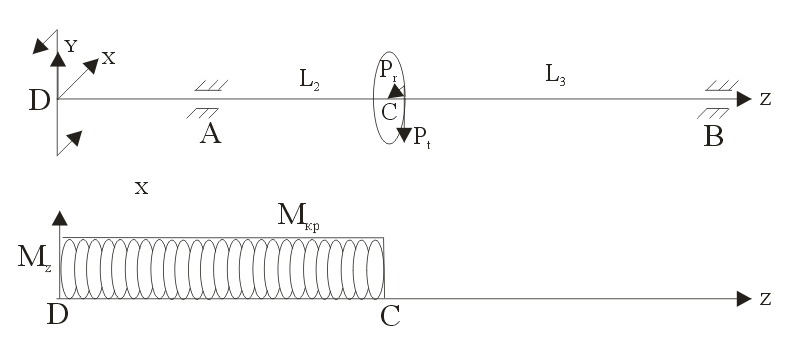
V. Изгиб в плоскости действия силы Рt.

1. Определим реакции опор YА и YВ
а) Равновесие моментов относительно опоры А
а) Из условия равновесия моментов относительно опоры А: ƩМA = 0 найдем реакцию в опоре YВ (момент, направленный против хода часовой стрелки, считается положительным)
- Pt L2 + YВ (L2 + L3) = 0 → YВ = Pt L2/(L2 + L3)
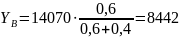 Н
Н
б) Из условия равновесия моментов относительно опоры В: ƩМВ = 0 найдем реакцию в опоре YА
- Pt L3 + YА (L2 + L3) = 0 → YА = Pt L3/(L2 + L3)
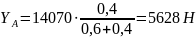
в) Проверка: равновесие сил на ось Y: ƩFy = 0
YА + YB – Pt = Pt L2/(L2 + L3) + Pt L2/(L2 + L3) – Pt = Pt - Pt = 0
2. Строим эпюру изгибающего момента Mt
a) Mt1 = 0
б) (А) 0 ≤ z ≤ L2 (C) Mt2 = YА z = z Pt L3/(L2 + L3) – линейная функция
При z = 0 (A) Mt = 0, при z = L2 (С) Mt(C) = Pt L2 L3/(L2 + L3)
Mt(C)
=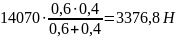
в) (В) 0 ≤ z ≤ L3 (C) Mt3 = YВ z = z Pt L2/(L2 + L3) – линейная функция
При z = 0 (В) Mt = 0, при z = L3 (С) Mt(C) = Pt L2 L3/(L2 + L3)
Mt(C)
=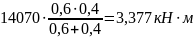
VI. Изгиб в плоскости действия силы Рr.
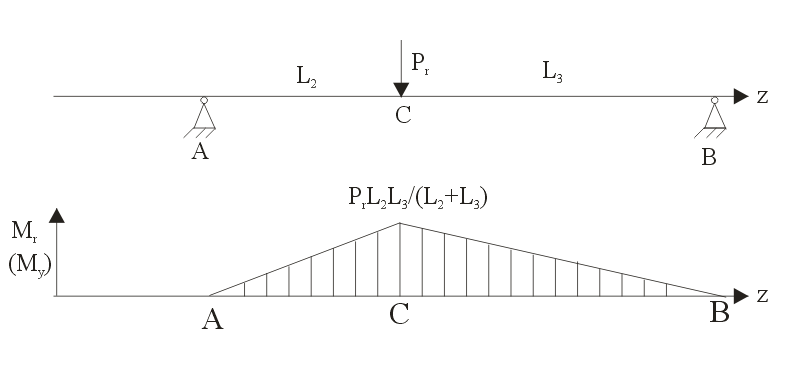
Так как сила Pr = 0.4 Pt то эпюра изгибающего момента Mr аналогична эпюре изгибающего момента Mt с заменой силы Pt на силу Pr
Mr(A) = 0, Mr(B) = 0, Mr(C) = Pr L2 L3/(L2 + L3)
Mr(C)
=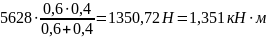
VII. Определим диаметр вала
1. Определим диаметр вала d1 из условия жесткости при кручении
Θ
= Δφ/L
= Mкр
/(G
Iρ)
≤ [dU]B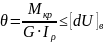 ,
,
где [dU]B – жесткость вала на кручение,
G – модуль упругости первого рода;
Iρ – полярный момент инерции сечения,
Iρ = πd4/32 = 0.1 d4.
Mкр /(G 0.1 d14) ≤ [dU]B → d1 ≥ {10 Mкр /(G [dU]B}1/4
d1
≥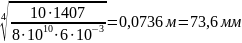
2. . Определим диаметр вала d2 из условия прочности при воздействии изгибающих и крутящего моментов
σэкв = Мэкв/Wx ≤ [σ]
где [σ] – допускаемое напряжение при изгибе,
момент
сопротивления вала при изгибе Wx
= πd3/32
= 0.1 d3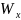 ,
,
эквивалентный момент Мэкв = (Mкр2 + Mt2 + Mr2)1/2
Мэквmax = Мэкв(C) = [Mкр2 + Mt2(C) + Mr2(C)]1/2
Мэквmax
= Мэкв(C)
=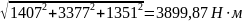
Mэкв(C)/(0.1 d23) ≤ [σ] → d2 ≥ {10 Mэкв(C)/[σ]}1/3
d2
≥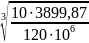 =0,0687 м=68,7 мм
=0,0687 м=68,7 мм
3. Определим диаметр вала d3 из условия жесткости при изгибе
ΔC ≤ [dS]B
Прогиб в точке С ΔC определяют прогиб Δt в плоскости действия силы Рt и прогиб Δr в плоскости действия силы Рr
ΔC = (Δt2 + Δr2)1/2
Так как сила Pr = 0.4 Pt то прогиб Δr = 0.4 Δt и
ΔC = (Δt2 + (0.4Δt)2)1/2 = 1.08 Δt
Определим прогиб Δt в плоскости действия силы Рt в точке С
а). Грузовая эпюра Мp = Mt - построена

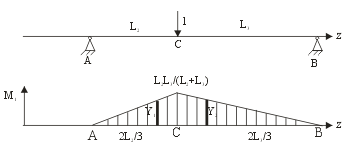
б). Строим вспомогательную систему (ВС) для определения перемещения в точке С в т. С прикладываем единичную силу
в). Единичная эпюра М1 аналогична эпюре изгибающего момента Mt с заменой силы Pt на единичную силу 1
M1(A)
= 0,
M1(B)
= 0,
M1(C)
=
L2
L3/(L2
+ L3)=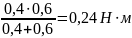
г). Определим перемещение Δt
Δt = ∫(Мp М1)/(ЕIx) = (A1Y1 + A2Y2)/(ЕIx) = Y(A1 + A2)/(ЕIx)
Значения Y1 и Y2 на линейной эпюре М1 из-за подобия треугольников с коэффициентом подобия 2/3 равны
Y1
= Y2
= Y
= (2/3) L2
L3/(L2
+ L3)=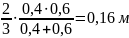
Площадь произвольной эпюры
A1
+ A2
= (1/2)
(L2
+ L3)
Pt
L2
L3/(L2
+ L3)
= (1/2)
Pt
L2
L3=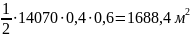
Следовательно
Δt = (2/3)L2L3/(L2+L3) (1/2)PtL2L3/(ЕIx) = (1/3)Pt(L2L3)2/[(L2+L3)ЕIx]
Δt
=
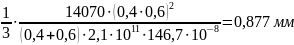
Ix – осевой момент инерции сечения,
Ix
= πd4/64
= 0.05 d4=
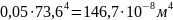
ΔC = 1.08 Δt = (1.08/3)Pt(L2L3)2/[(L2+L3)Е0.05d34] ≤ [dS]B
d3 ≥ {(0.36)Pt(L2L3)2/[(L2+L3)Е0.05[dS]B}1/4
d3
≥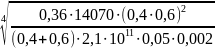 = 0,06105 м = 61,1мм
= 0,06105 м = 61,1мм
4. Выбираем из трех значений диаметра максимальное
d=max
(d1,
d2,
d3)
=
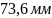
Расчёт подшипников и подбор
Подшипники служат опорами концов валов и вращающихся осей. Подшипники уменьшают трение в опорах и воспринимают радиальные и осевые нагрузки от сил, действующих на валы и оси. Подшипниковая опора обеспечивает минимальные потери мощности в машине, так как коэффициент полезного действия пары подшипников, поддерживающих вал, равен 99%.
У
 словия
работы: t<100
℃ ; средний уровень вибрации.
словия
работы: t<100
℃ ; средний уровень вибрации.
=![]() 1,3 – 1,5 = 1,4 Lh
≈ 20000 ч
1,3 – 1,5 = 1,4 Lh
≈ 20000 ч
= 1
В результате определения реакций опор находим значения X A, YA, XB, YB. После этого определяем радиальные нагрузки на подшипниковые узлы:
YA
=
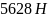
XA = 0,4 YA = 2251,2 Н
YB
=
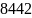 Н
Н
XB = 0,4 YB = 3376,8 Н
=![]() 6061,5Н
6061,5Н
= 9092,3Н
Определяется эквивалентная нагрузка РЭ на подшипниковый узел:
![]()
9092,3∙ 1∙ 1∙ 1 ∙ 1,3 = 11819,99 Н
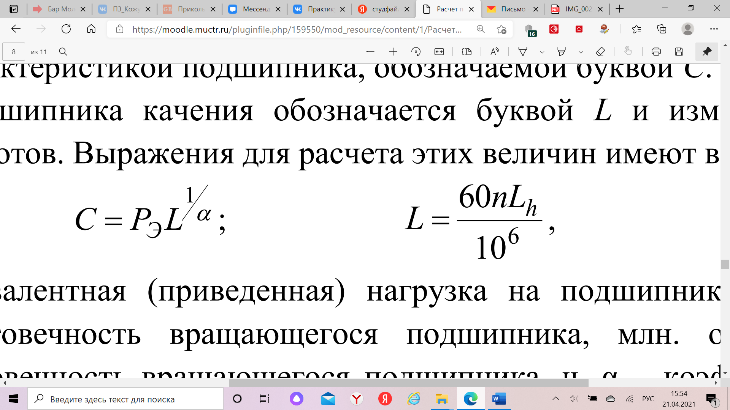 =
=
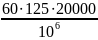 =
150
млн. оборотов
=
150
млн. оборотов
![]()
=
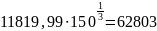 Н
Н
d=max (d1, d2, d3) = 73,6 мм
d = 75 мм
Подшипник 115 из таблицы 1:
С
=
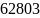 > C
= 39700
> C
= 39700
Вывод: подшипник не подходит
Подшипник 215 из таблицы 2:
С = < C = 66300
Вывод: подшипник подходит.
Следует использовать в качестве опор шариковые радиальные
однорядные подшипники 215, легкой серии диаметров 2, узкая серия ширин 0 с характеристиками:
d = 75 мм, D = 130 мм, B = 25 мм, r = 2,5 мм.
