2020 Экзамен / Приложение 1
.docПриложение 1
Обзор основных методов интегрирования
№ п/п |
Вид интеграла |
Метод интегрирования |
1 |
|
Подстановка
|
2 |
|
Интегрирование
по частям:
Метод
интегрирования по частям применяется,
например, к интегралам вида
|
3 |
|
Подстановка
|
4 |
где
|
Подынтегральную дробь представляют в виде суммы простейших дробей
|
5 |
где
|
Приводится к
интегралу от рациональной дроби
подстановкой
|
6 |
где – рациональная функция своих аргументов |
Сводится к интегралу от рациональной дроби подстановкой
|
7 |
|
Подстановкой
|
8 |
где
–
рациональная функция от
|
Приводится к
интегралу от рациональной дроби
подстановками Эйлера:
где
|
9 |
где
|
Записываем
равенство
где
|
10 |
|
Этот интеграл
приводится подстановкой
|
11 |
где
|
Интеграл от биномиального дифференциала выражается через элементарные функции только при выполнении одного из следующих условий; 1)
если
2)
если
3)
если
(см. 1.6) |
12 |
|
Универсальная
подстановка
Если
то
подстановка
Если
то
подстановка
Если
то
подстановка
|
13 |
|
Применяется
подстановка
|
Приложение 2
Гиперболические функции
Во многих приложениях
математического анализа встречаются
комбинации показательных функций вида
 и
и
 .
Эти комбинации рассматриваются как
новые функции и обозначаются так:
.
Эти комбинации рассматриваются как
новые функции и обозначаются так:
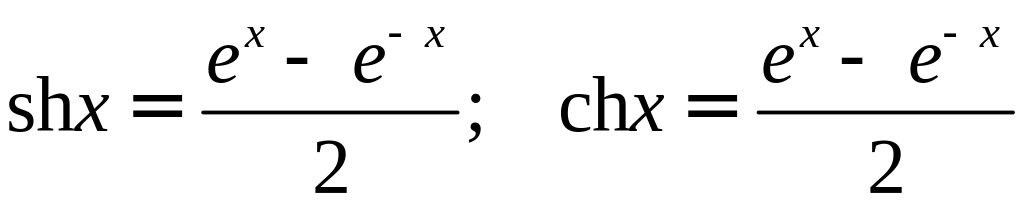 .
.
Первую из этих функций называют гиперболическим синусом, вторую – гиперболическим косинусом. С помощью этих функций можно определить еще две функции
 и
и
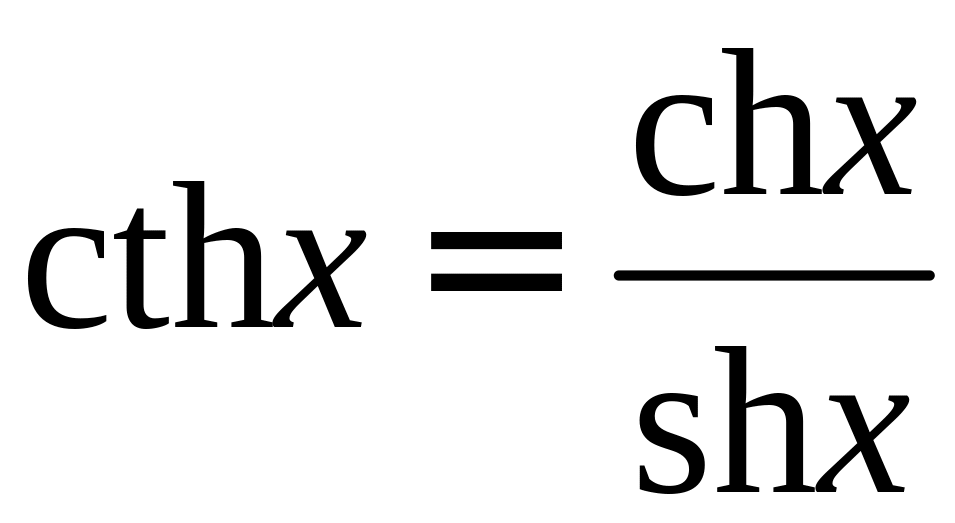 :
:
 – гиперболический
тангенс,
– гиперболический
тангенс,
 – гиперболический
котангенс.
– гиперболический
котангенс.
Функции
![]() определены для всех значений
.
Функция
определены для всех значений
.
Функция
![]() определена всюду, за исключением точки
определена всюду, за исключением точки
![]() .
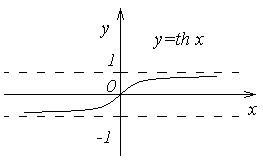
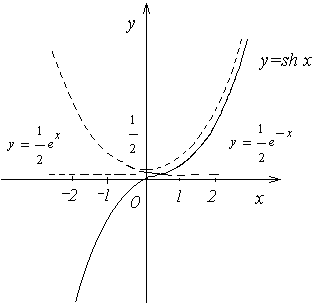
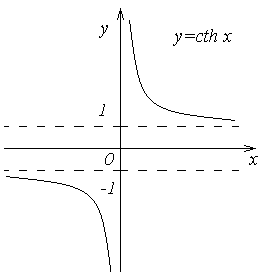
Графики гиперболических функций
представлены на рис. 1, 2, 3, 4.
.
Графики гиперболических функций
представлены на рис. 1, 2, 3, 4.
Рис. 1
Рис. 3 |
Рис. 2
Рис. 4 |
Из определения
функций
![]() и
и
![]() следуют соотношения, аналогичные
соотношениям между соответствующими
тригонометрическими функциями:
следуют соотношения, аналогичные
соотношениям между соответствующими
тригонометрическими функциями:
![]() (1)
(1)
![]() (2)
(2)
![]() . (3)
. (3)
Действительно,
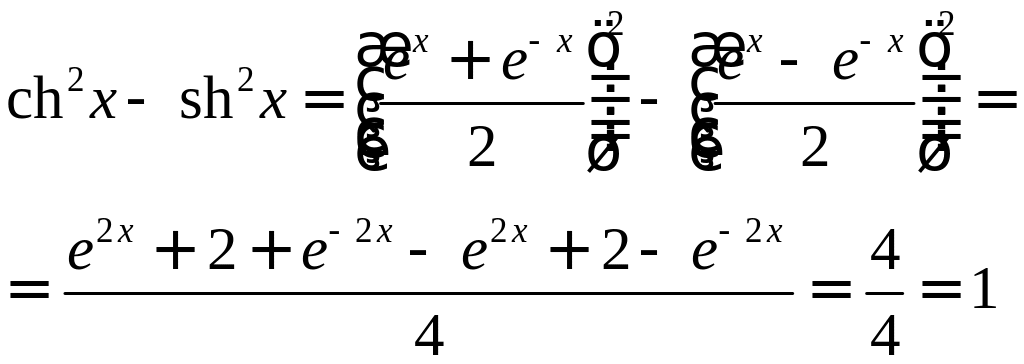
Далее, заметив,
что
 получаем
получаем


 .
.
Аналогично доказывается и соотношение (3).
Если в формулах
(2) и (3) считать
![]() получим следующие соотношения:
получим следующие соотношения:
![]() (4)
(4)
![]() . (5)
. (5)
Из формулы (1) имеем
![]()
![]() .
.
Подставляя
поочередно
![]() и
и
![]() в (4) получим
в (4) получим
![]()
![]() .
.
Эти соотношения дают, так называемые, формулы понижения порядка:
 (6)
(6)
 . (7)
. (7)
Название
«гиперболические функции» объясняется
тем, что функции
![]() и
и
![]() играют ту же роль для параметрического
представления гиперболы
играют ту же роль для параметрического
представления гиперболы
![]() ,
,
какую тригонометрические
функции
![]() и
и
![]() – для параметрического представления
окружности
– для параметрического представления
окружности
![]() .
.
Действительно,
исключая параметр
![]() из уравнений
из уравнений
![]() ,
получим
,
получим
![]() ,
или
,
или
(уравнение окружности).
Аналогично,
уравнения
![]() являются параметрическими уравнениями
гиперболы.
являются параметрическими уравнениями
гиперболы.
Действительно,
возводя в квадрат эти уравнения и вычитая
из первого второе, получим
![]() ,
отсюда
,
а это и есть уравнение гиперболы.
,
отсюда
,
а это и есть уравнение гиперболы.
Производные гиперболических функций определяются формулами
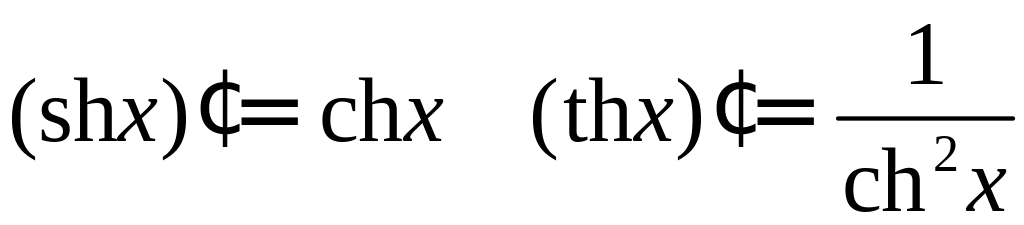
 ,
,
которые вытекают
из самого определения гиперболических
функций; например, для
 имеем
имеем
 .
.

 ,
,

 ,
,



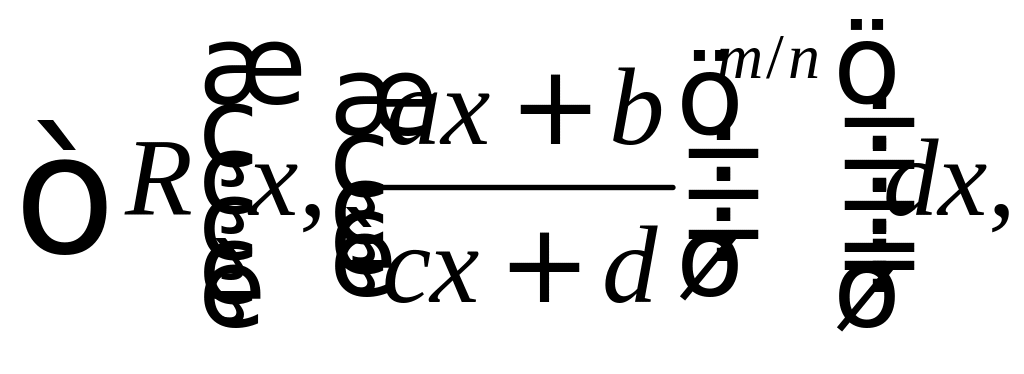


 интеграл приводится к сумме двух
интегралов:
интеграл приводится к сумме двух
интегралов:
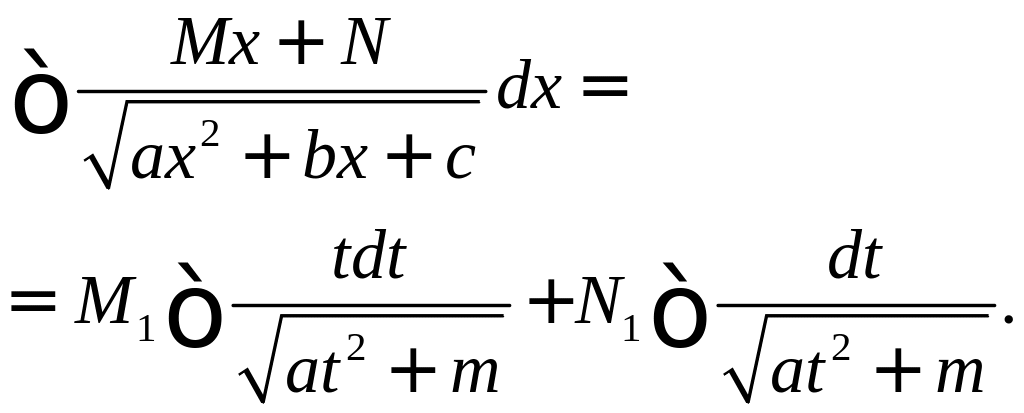
 ,
,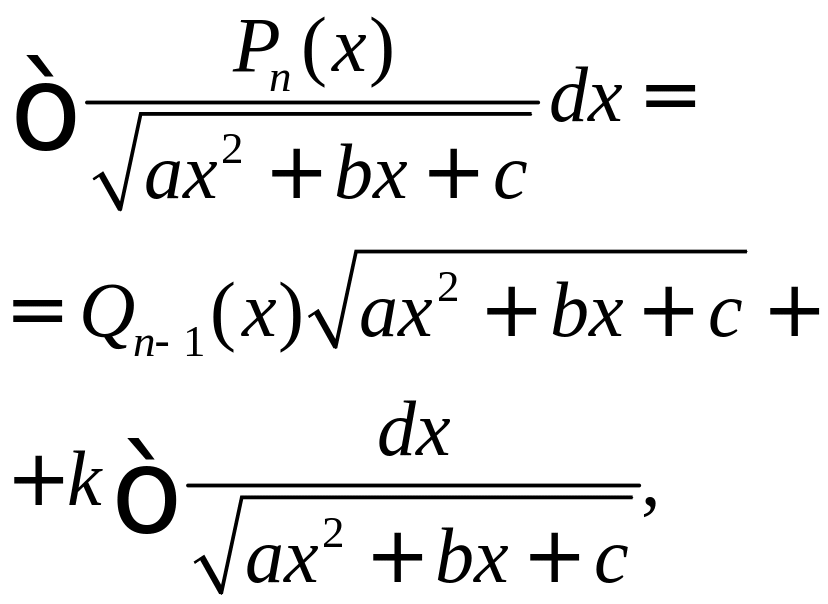

 – целое число,
– целое число, – целое число,
– целое число,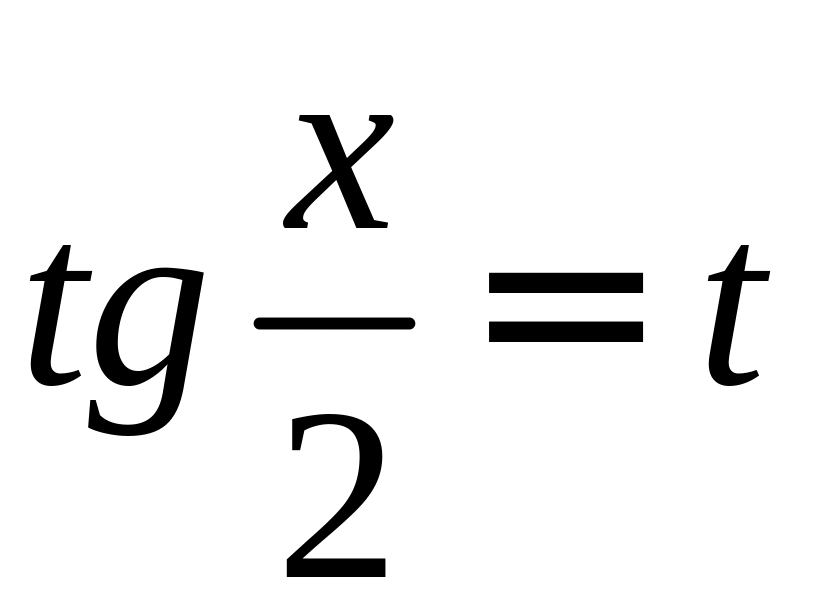 .
. .
При этом
.
При этом
 .
.