Глава 1 неопределенный интеграл

1.1. Основные понятия

Определение 1. Функция называется первообразной для функции на , если при любом имеем .

Замечание. Если – первообразная для , то также первообразная для , так как .

Определение 2. Совокупность всех первообразных функций для функции на интервале называется неопределенным интегралом от функции . Эта совокупность обозначается символом (читается: интеграл от ).

Если – какая-нибудь одна первообразная для функции , то можно записать

,

где – произвольная постоянная.

. Основные правила интегрирования.

1. , где – постоянная величина.

2. где постоянная величина.

3.

4. Если и , то

.

В частности,

.

. Таблица простейших интегралов.

1. ,

2.

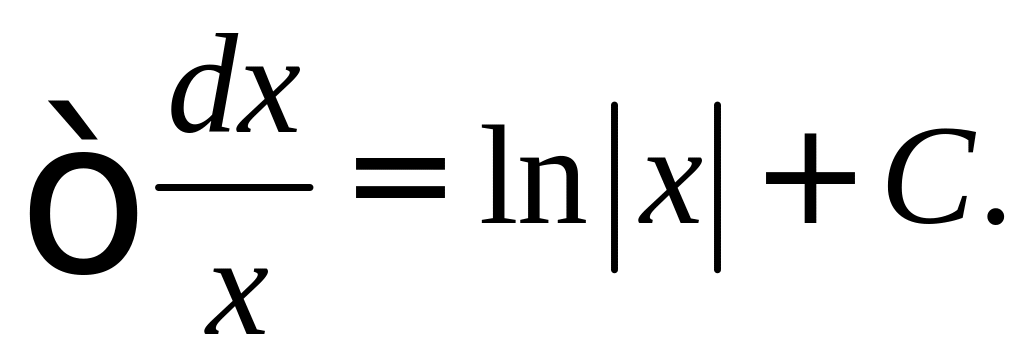
3.

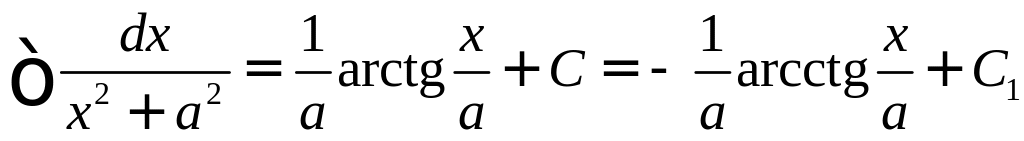
4.

5.

6.

7. , .

8. .

9. .

10. .

11. .

12. .

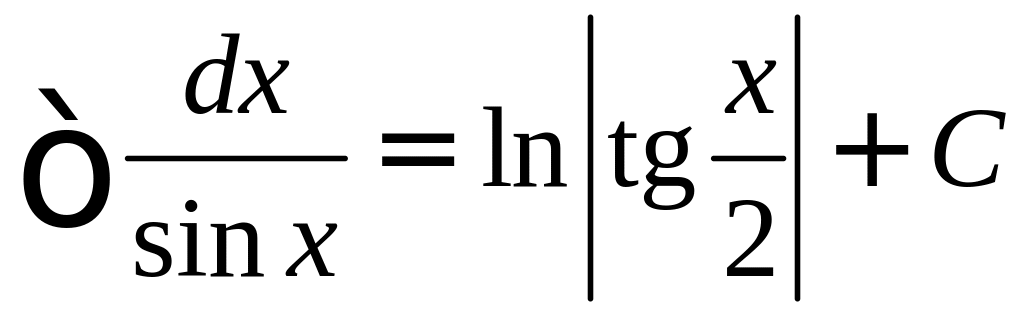13. .

14. .

15. .

16. .

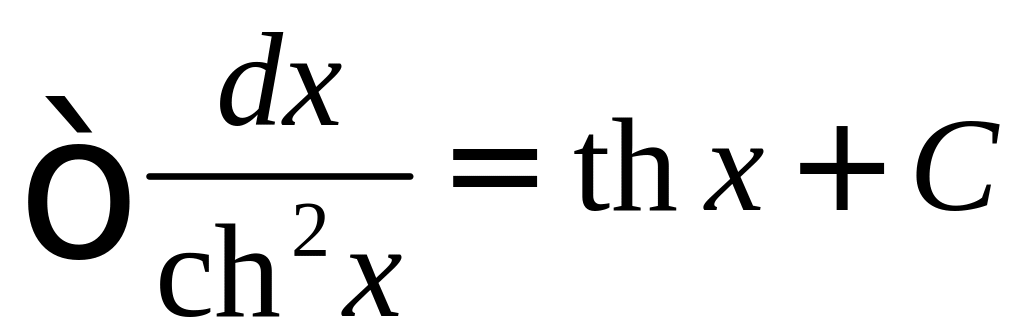17. .

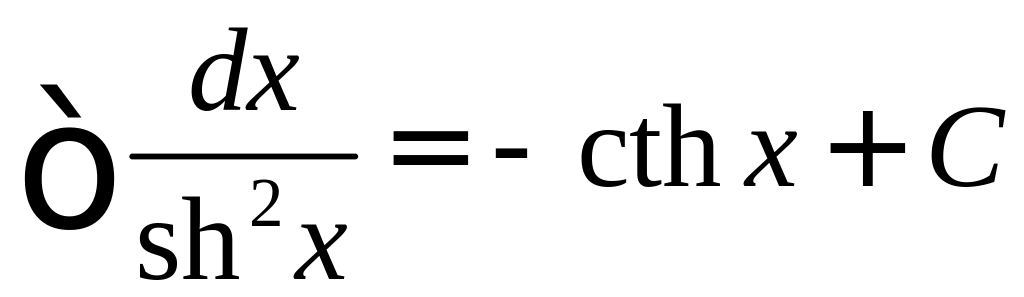Пример 1.

.

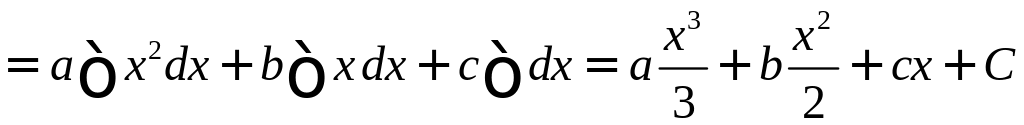. Интегрирование путем подведения под знак дифференциала.

Правило 4 значительно расширяет таблицу простейших интегралов. А именно, в силу этого правила таблица интегралов оказывается справедливой независимо от того, является переменная интегрирования независимой переменной или дифференцируемой функцией.

Пример 2.

,

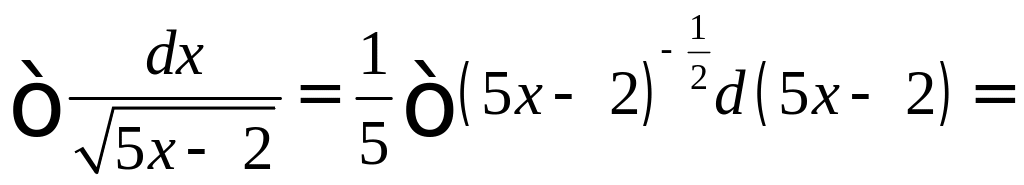
где . Использовалось правило 4 и табличный интеграл 1.

Пример 3. ,

Здесь использовался табличный интеграл 5 и равенство .

Пример 4. в силу правила 4 и табличного интеграла 7.

Пример 5.

В примерах 2, 3, 4, 5 прежде чем использовать тот или иной табличный интеграл, мы приводили данный интеграл к виду

, где .

Такого рода преобразование называется подведением под знак дифференциала.

Полезно отметить часто применяемые преобразования дифференциалов, которые, в частности, использовались в этих примерах:

а)

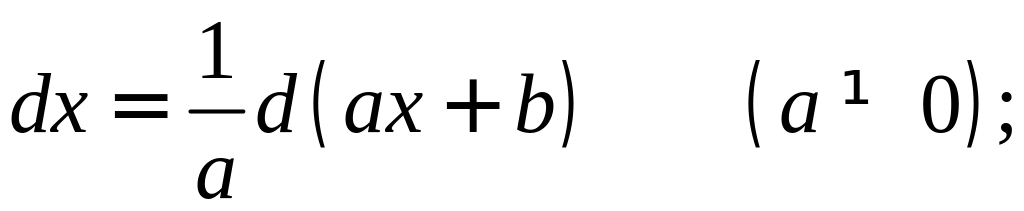
б) и т.п.

1.2. Метод подстановки

1^o. Замена переменной в неопределенном интеграле.

Полагая

,

где – новая переменная и – непрерывно дифференцируемая монотонная функция, будем иметь:

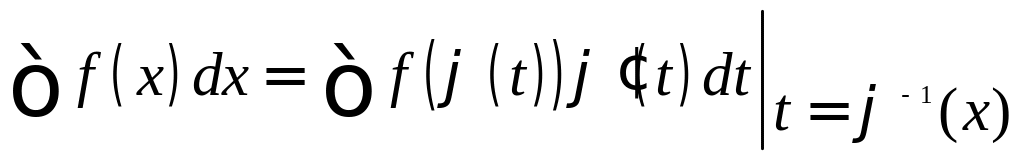. (1)

Функцию стараются выбирать таким образом, чтобы правая часть формулы (1) приобрела удобный для интегрирования вид.

Пример 6. Найти .

Решение. Обозначим , тогда . Получим

.

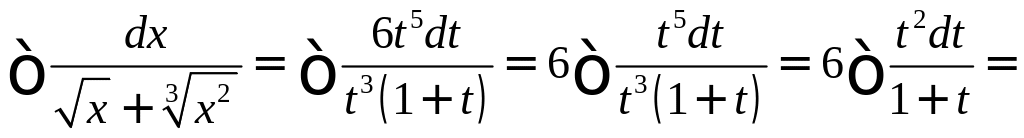
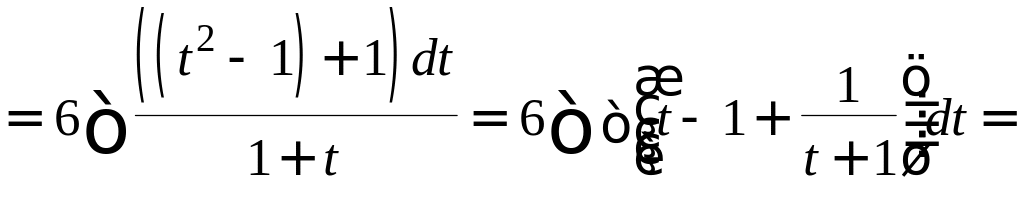
Возвращаясь к исходной переменной , получим

.

Чаще используется подстановка вида , где монотонная непрерывная функция, откуда находится , причем функция должна быть непрерывно дифференцируемой. После чего находим .

Пример 7. Найти .

Решение. Естественно положить , отсюда , и Следовательно,

.

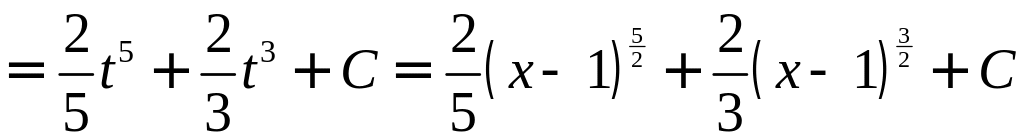Замечание. Если подынтегральная функция имеет вид , как правило, этот корень надо взять за .

Пример 8. Найти .

Решение. Сделаем подстановку , тогда , ; получим

.

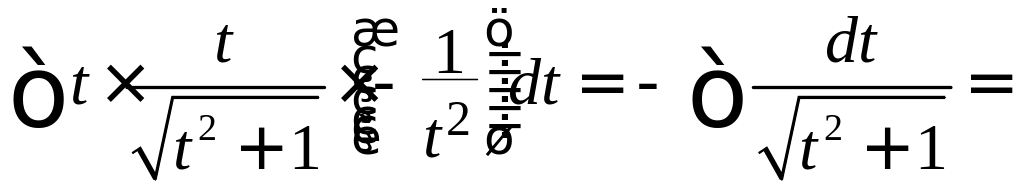
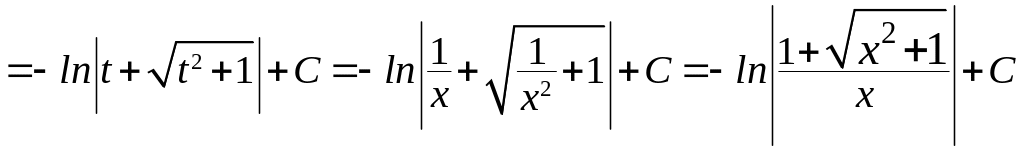Замечание. Если подынтегральное выражение имеет вид , то есть в знаменателе стоит корень квадратный из квадратного трехчлена и перед ним линейный множитель в какой-то степени, то всегда берется замена .

Пример 9. Найти .

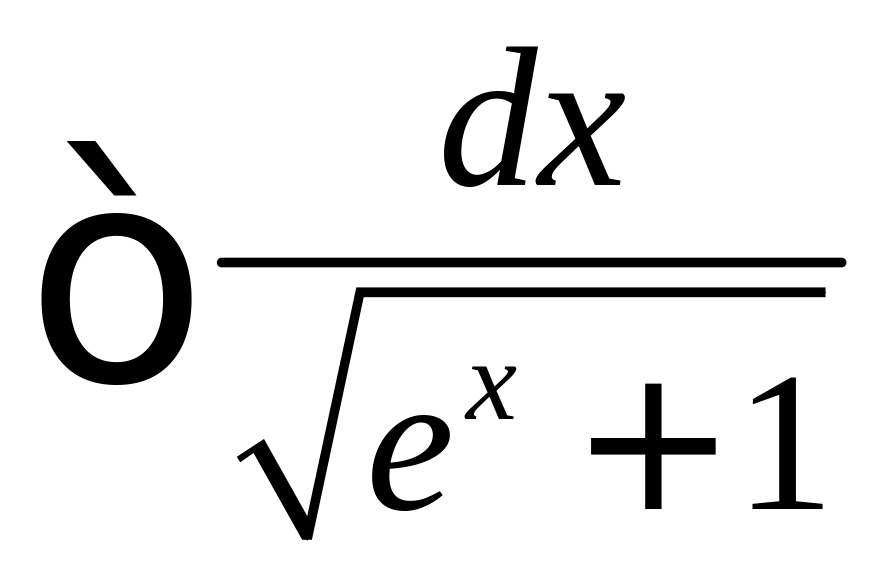Решение. Сделаем замену , тогда ; ; (воспользовались тем, что ). В результате получаем

.

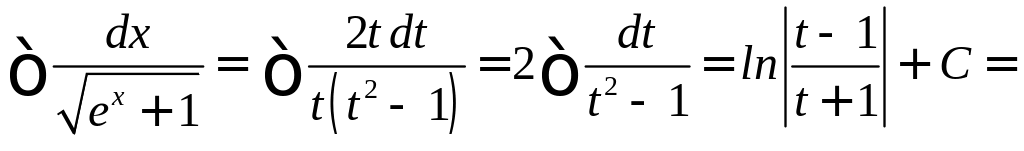
Пример 10. Найти .

Решение. Обозначим , , продифференцировав обе части этого равенства, получим, , откуда

.

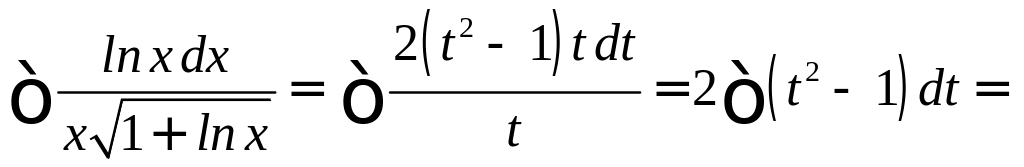
. Тригонометрические подстановки.

Подстановки типа используются часто для вычисления интегралов, которые содержат корни вида: ; ; , и в этом случае они называются тригонометрическими подстановками.

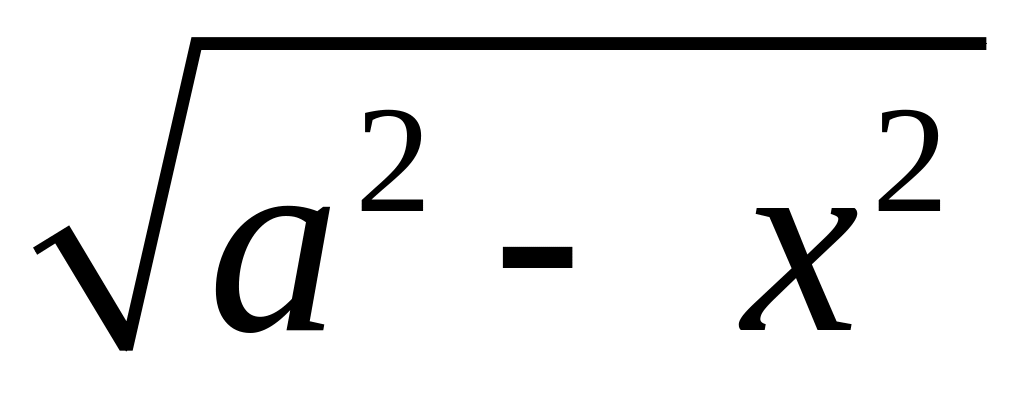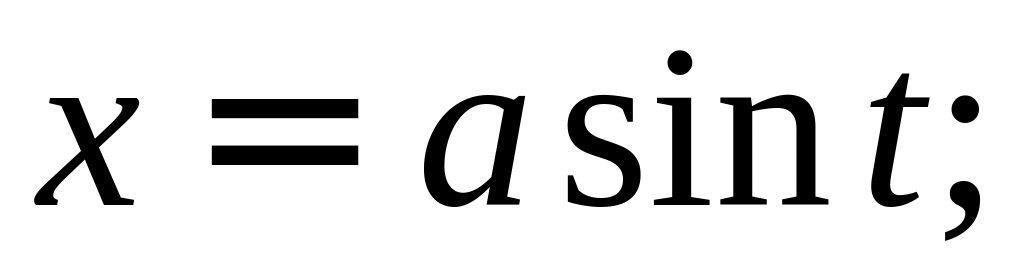1. Если интеграл содержит радикал , то обычно полагают константу здесь и в остальных случаях полагают положительной, , тогда

.

так как при .

2) Если интеграл содержит радикал , то полагают , где

.

3) Если интеграл содержит радикал то полагают . Здесь 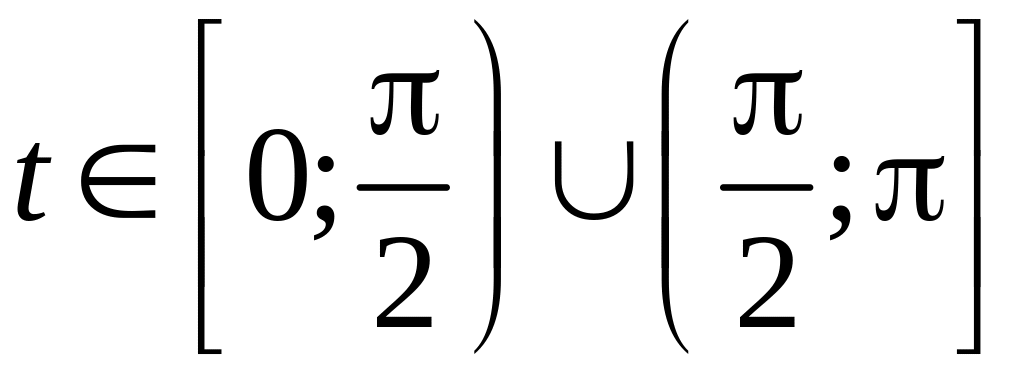, поэтому

Пример 11. Найти .

Решение. Применим подстановку , тогда , , , .

.

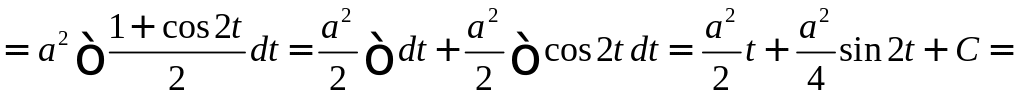
Пример 12. Найти

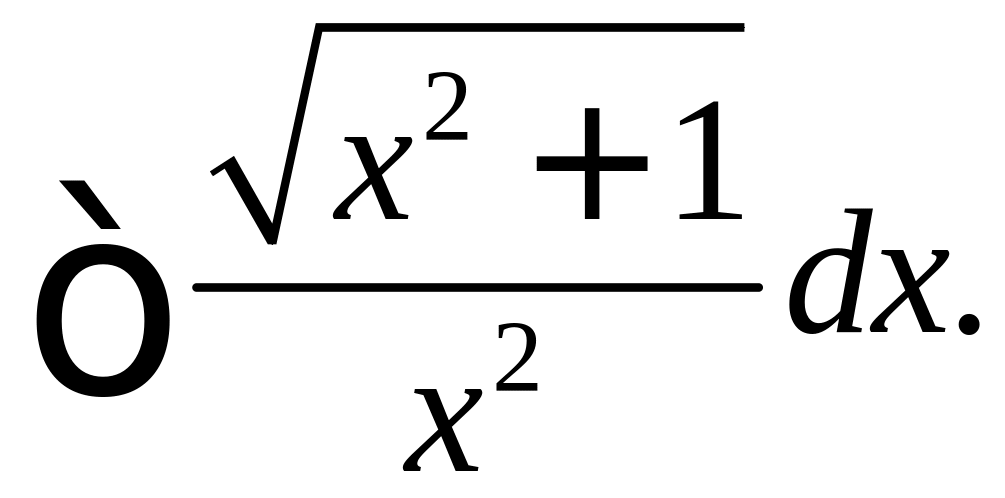
Решение. Полагаем Следовательно,

,

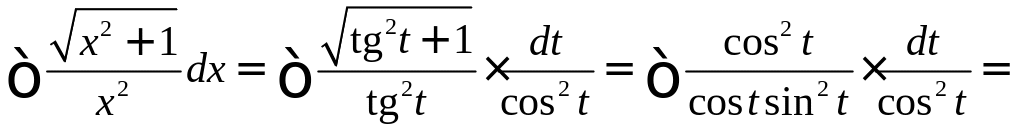
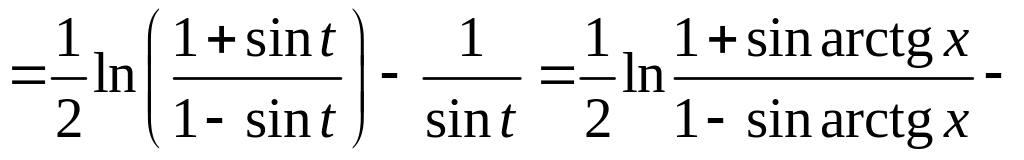
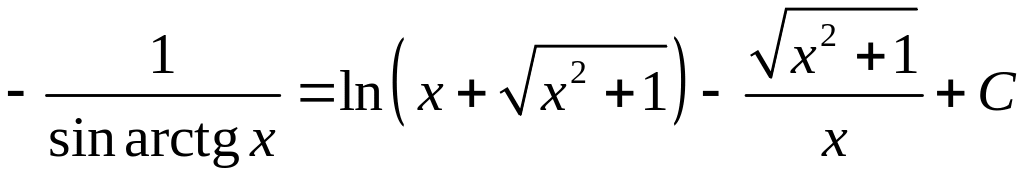так как .

Кроме стандартных тригонометрических подстановок могут быть использованы и другие подстановки, позволяющие избавиться от корня, например, .

Пример 13. Найти .

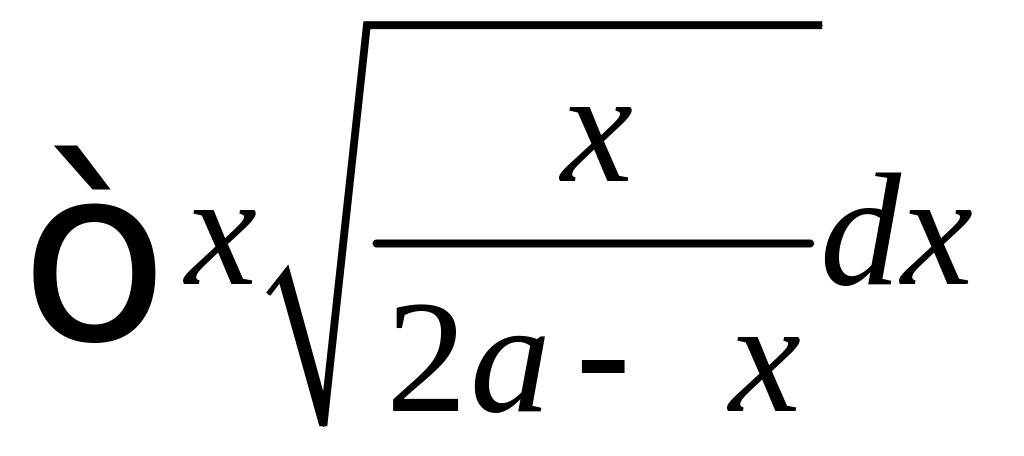Решение. Возьмём , где , тогда , а подынтегральная функция примет вид:

.

Имеем

.

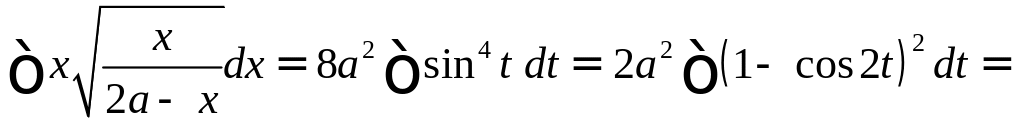
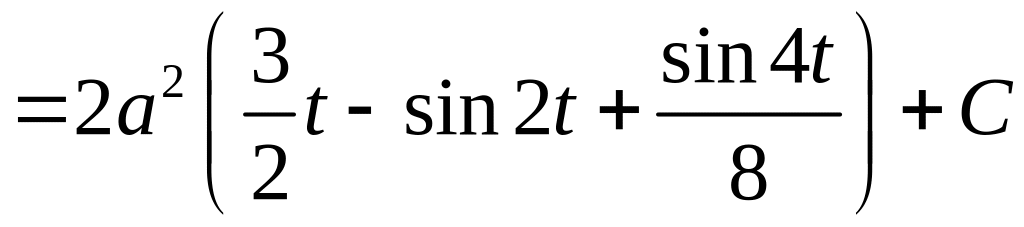Вернёмся к исходной переменной , , .

.

.

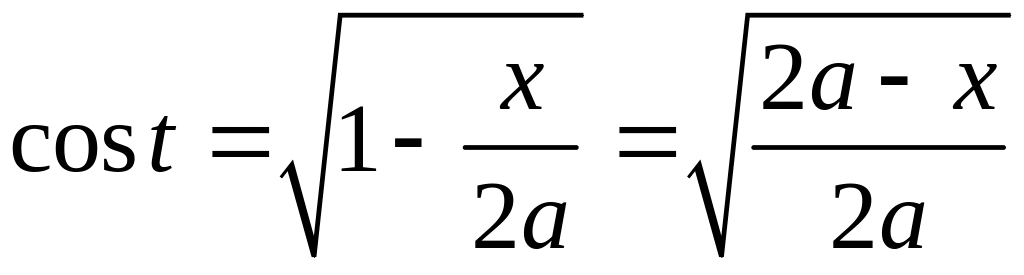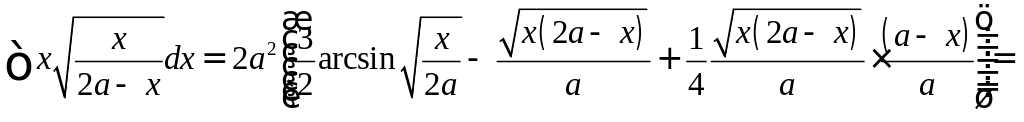
Наряду с тригонометрическими подстановками используются гиперболические подстановки.

1) Если интеграл содержит , то полагают , тогда (так как ).

2) Если интеграл содержит , то полагают , тогда так как .

Пример 14. Найти ,

применяя гиперболическую подстановку .

Решение. Имеем и .

Отсюда

.

Вернёмся к исходной переменной

,

осталось найти . Так как , поэтому , .

Окончательно получаем:

.
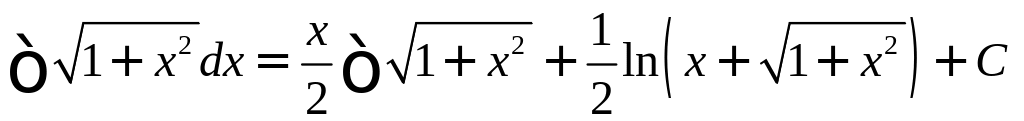