Добавил:

Rei Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Авиационный Технический Университет

Предмет:

Математический анализ

Файл:

2020 Экзамен / Определенные интегралы

.pdf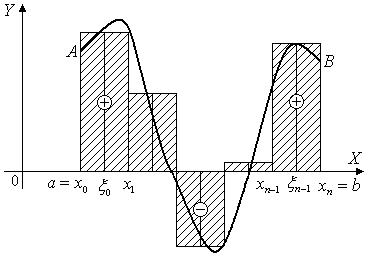

Скачиваний:

Добавлен:

09.06.2022

Размер:

304.39 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

§ 1. Определенный интеграл как предел суммы

1 . Интегральная сумма. Пусть функция f (x) определена на от-

резке a ≤ x ≤ b и a = x0 < x1 <... < xn =b – произвольное	разбиение
этого отрезка на n частей (рис. 1). Сумма вида
Sn = n∑−1 f (ξi )∆xi ,	(1)
t =0
где
xi ≤ ξi ≤ xi+1; ∆xi = xi+1 − xi ;
i = 0,1,2,...,(n −1),

называется интегральной суммой функции f (x) на [a,b]. Геометрически Sn представляет собой алгебраическую сумму площадей соответствующих прямоугольников (см. рис. 1).

2 . Определенный интеграл. Предел суммы Sn при условии,

что число разбиений n стремится к бесконечности, а наибольшая из разностей ∆xi

– к нулю, называется

определенным инте-

гралом функции f (x)

впределах от

x= a до x = b, т.е.


		n∑−1 f (ξi )∆xi = ∫b		Рис. 1
lim		n∑−1 f (ξi )∆xi = ∫b		f (x)dx .	(2)
max ∆xi	→0 i=0		a
Если функция f (x)		непрерывна на [a,b], то она интегрируема на
[a,b], т.е. предел (2)		существует и не зависит от способа разбиения

промежутка интегрирования [a,b] на частичные отрезки и от выбора точек ξi на этих отрезках. Геометрически определенный интеграл (2)

представляет собой алгебраическую сумму площадей фигур, составляющих криволинейную трапецию aABb, в которой площади частей, расположенных выше оси OX , берутся со знаком плюс, а площади частей, расположенных ниже оси OX , – со знаком минус (см. рис. 1).

Определения интегральной суммы и определенного интеграла естественно обобщаются на случай отрезка [a,b], где a >b.

§2. Вычисление определенных интегралов

спомощью неопределенных.

1 . Определенный интеграл с переменным верхним пределом.

Если функция f (t) непрерывна на отрезке [a,b], то функция

F(x)= ∫x f (t)dt

есть первообразная для функции f (x), т.е.

F′(x)= f (x) при a ≤ x ≤b .

. Формула Ньютона-Лейбница. Если F

(x)

= f (x), то

′

f (x)dx = F(x)

= F(b)− F(a).

∫

Первообразная F(x)a

вычисляется путем нахождения неопределенно-

го интеграла

∫ f (x)dx = F(x)+C .

Пример 1. Найти интеграл

∫x4dx.

−1

(−1)5

Решение.

3 4

= 48

∫x

dx =

−1

−

−1

3 . Замена переменой в определенном интеграле.

Если функция f (x) непрерывна на отрезке a ≤ x ≤b и x = ϕ(t) – функция, непрерывная вместе со своей производной ϕ′(t) на отрезке

a ≤t ≤b где a = ϕ(a) и b = ϕ(β) , причем f

(ϕ(t)) определена и непре-

рывна на отрезке a ≤t ≤b , то

( )

( (

))

( )

∫

′

f x dx = f ϕ t

t dt .

Пример 1. Найти

(a >0).

∫x2 a2 − x2 dx

Решение. Положим

x = asin t;

dx = acos t dt.

Тогда t = arcsin

и, следовательно, можно принять

π. Поэтому будем иметь:

a = arcsin0 = 0,

β = arcsin1 =

∫x2

a2 − x2 dx = 2∫a2 sin2 t

a2 −a2 sin2 t acost dt =

= a4

2 t cos2 t dt = a

∫sin

∫sin2 2t dt = a

∫(1−cos4t)dt =

π/ 2

πa4

t −

sin 4t

4 . Интегрирование по частям.

Если функции u(x) и v(x) непрерывно дифференцируемы на отрезке [a,b], то

∫b u(x)v(x)dx = u(x)v(x)	b	− ∫b v(x)u′(x)dx	(1)

a	a	a

§ 3. Теорема о среднем значении

1 . Оценки интегралов. Если f (x)≤ F(x) при a ≤ x ≤b , то

	b∫ f (x)dx ≤ b∫F(x)dx .		(1)
Если f (x) и ϕ(x)	a	a
	непрерывны при a ≤ x ≤b и, кроме того, ϕ(x)≥ 0,
то
m∫b ϕ(x)dx ≤ ∫b		f (x)ϕ(x)dx ≤ M ∫b ϕ(x)dx.	(2)
a	a	a	f (x) на
где m − наименьшее, а M − наибольшее значение функции

отрезке [a,b].

В частности, если ϕ(x)≡1, то

m(b −a)≤ b∫ f (x)dx ≤ M (b −a).

(3)

Неравенства (2) и (3) можно соответственно заменить эквивалентными им равенствами:

∫b	f (x)ϕ(x)dx = f (c)∫b ϕ(x)dx
a	a
и	b∫ f (x)dx = f (ξ)(b −a),
	b∫ f (x)dx = f (ξ)(b −a),
	a

где c и ξ - некоторые числа, лежащие между a и b. Пример 1. Оценить интеграл

π
I = 2∫			dx.
I = 2∫	1+	1 sin2 x	dx.
0		2
0

Решение. Так как 0 ≤sin2 x ≤1, то имеем:

π2 < I < π2 32 ,

т.е.

1,57 < I <1,91.

2 . Среднее значение функции. Число

µ = 1 b∫ f (x)dx b −a a

называется средним значением функции f (x) на отрезке a ≤ x ≤b .

§4. Несобственные интегралы

1 . Интегралы с бесконечными пределами (1 рода)

Несобственные интегралы с бесконечными пределами (или 1 рода) определяются следующим образом:

+∞	lim	b		b	lim	b	(1)
∫ f (x)dx =	lim	∫ f (x)dx,		∫ f (x)dx =	lim	∫ f (x)dx,	(1)
a	b→+∞a			−∞	a→−∞a
+∞	lim	c		b
∫ f (x)dx =	lim	∫ f (x)dx + lim		∫ f (x)dx ,
−∞	a→−∞a		b→+∞c

где c − произвольное число (обычно c = 0).

Несобственные интегралы 1 рода называются сходящимися, если существуют конечные пределы, стоящие в правых частях равенства (1). Если же указанные пределы не существуют или бесконечны, то несобственные интегралы называются расходящимися.

Вот некоторые признаки сходимости и расходимости несобственных интегралов 1 рода:

1. Если на промежутке непрерывные функции f (x) и ϕ(x) удовле-

творяют условию 0 ≤ f (x)≤ϕ(x), то			из	сходимости	интеграла
+∞			+∞
∫ϕ(x)dx следует сходимость интеграла			∫ f (x)dx, а из расходимо-
a			a
	+∞				+∞
сти интеграла ∫ f (x)dx следует расходимость интеграла					∫ϕ(x)dx
	a				a
(«признак сравнения»).
2. Если при x [a;+∞), f (x)> 0, ϕ(x)> 0 и существует конечный
	f (x)		+∞	+∞
предел lim	f (x)	= k ≠ 0, то интегралы	∫ f	(x)dx и ∫ϕ(x)dx схо-
предел lim		= k ≠ 0, то интегралы	∫ f	(x)dx и ∫ϕ(x)dx схо-
x→+∞ ϕ(x)			a	a

дится и расходятся одновременно, («предельный признак сравнения»).

+∞

3. Если сходится интеграл

∫

(x)

dx , то сходится интеграл

∫ f (x)dx,

который в этом случае называется абсолютно сходящимся.

Пример 1. Вычислить несобственный интеграл

+∞ dx

или уста-

∫

новить его расходимость.

Решение. По определению несобственного интеграла 1 рода

имеем:

+∞ dx

= lim

−

∫

2 = lim

= lim −

+ lim

=1,

b→∞

интеграл сходится и его величина равна 1.

Замечание. Можно показать, что интеграл

+∞ dx

сходится при

∫

α >1 и расходится при α ≤1.

Пример 2. Исследовать сходимость несобственного интеграла

∫xcos xdx .

−∞ Решение. По определению несобственного интеграла I рода

u = x

du = dx

∫ xcos xdx =

αlim→−∞∫xcos xdx =

−∞

dv = cos xdx

v = sin x

+cos x

− lim cosa

= lim xsin x

= 0 − lim asin a +1

α→−∞

интеграл расходится, т.к. lim

asin a,

lim

cos a не существуют.

Пример 3.

α→−∞

+∞

Вычислить несобственный интеграл −∞∫

1+ x2

Решение. Подынтегральная функция f (x)=1+1x2 определена и

непрерывна на всей числовой оси. Кроме того, она является четной. Следовательно,

∞∫ f (x)dx = 2∞∫ f (x)dx .

−∞ 0

Исходя из определения несобственного интеграла (2.1), имеем

+∞

= lim

+∞

lim arctg x

−0 =

∫

1+ x2

+ x2

α→−∞

α→+∞

интеграл сходится. Следовательно, исходный интеграл также сходится и равен π.

Пример 4. Исследовать на сходимость интеграл +∫∞ x +2 dx.

1 3 x2

Решение.

Здесь

f (x)=

x +

> 0

при

x [1;+∞),

при

этом

x +

+∞

= ϕ(x). Но интеграл ∫

расходится так как

1 3 x2

∞

= lim 3x3

b =3 lim b3 −3 = ∞.

∫ dx

a 3

b→∞

+∞ x

расхо-

Поэтому,

согласно признаку сравнения,

интеграл ∫

дится.

+∞

Пример 5. Исследовать на сходимость интеграл

1∫

2 + x +3x5

Решение.

Здесь

f (x)=

> 0.

Рассмотрим

функцию

2 + x +3x5

ϕ(x)=

+∞

dx5

, интеграл от которой ∫

сходится. А так как существует

предел

lim

f (x)

= lim

≠ 0, то исходный интеграл

+ x +3x5

+∞

x→+∞ ϕ(x)

x→+∞ 2

также сходится («предельный признак сравнения»).

1∫

+ x +3x5

2 . Интегралы от неограниченных функций (II рода)

Если функция y = f (x) непрерывна в промежутке [a;b) и имеет

разрыв II-го рода при x =b, то несобственный интеграл от неограниченной функции (II рода) определяется следующим образом:

b	f (x)dx = lim	b−ε	(2)
∫	f (x)dx = lim	∫ f (x)dx .	(2)
a	ε→0	a

Если предел, стоящий в правой части равенства (2) существует, то несобственный интеграл II рода называется сходящимся; в против-

ном случае – расходящимся.

Аналогично, если функция y = f (x) терпит бесконечный разрыв

в точке x = a , то полагают
	b∫ f	(x)dx = lim		b∫ f (x)dx .		(3)
	a		ε→0a+ε
Если функция y = f (x)		терпит разрыв II-го рода во внутренней
точке c [a;b], то несобственный интеграл второго рода определяет-
ся формулой
∫b	f (x)dx =∫c		f (x)dx + ∫b		f (x)dx	(4)
a		a		c
В этом случае интеграл называется сходящимся, если оба несоб-
ственных интеграла, стоящих справа, сходятся.
Приведем некоторые признаки сходимости и расходимости для
несобственных интегралов второго рода.				(x) и ϕ(x) непрерывны, при
1. Если на промежутке [a;b)		функции f
x =b терпят разрыв II-го			рода	и	удовлетворяют	условию

0 ≤ f (x)≤ ϕ(x), то из сходимости интеграла b∫ϕ(x)dx следует схо-

димость интеграла b∫ f (x)dx , а из расходимости интеграла b∫ f (x)dx

			a			a
следует расходимость интеграла b∫ϕ(x)dx («признак сравнения»).
			a
2. Пусть функции			f (x) и ϕ(x) непрерывны на промежутке [a;b) и в
точке x =b терпят разрыв II-го рода.				Если существует предел
lim	f (x)	= k,	0 < k < +∞, то интегралы	b∫ f (x)dx	и	b∫ϕ(x)dx схо-

x→+∞ ϕ(x)				a		a

дятся или расходятся одновременно («предельный признак сравнения»).

3. Если функция f (x), знакопеременная на отрезке [a;b), имеет раз-

рыв в точке x =b, и несобственный интеграл b∫ f (x)dx сходится,

то сходится и интеграл b∫ f (x)dx .

Замечание. В качестве эталона для сравнения функций часто берут функцию ϕ(x)= (b −1x)α . Можно показать, что несобственный инте-

грал

(α > 0)

сходится при α <1 и

(5)

a∫(b − x)α

расходится приα ≥1.

Это же относится и к интегралам a∫

(x −a)α

Пример 6. Вычислить несобственный интеграл ∫

или

9 − x2

установит его расходимость.

Решение.

Подынтегральная функция терпит разрыв при

x =3

lim

= +∞ . Согласно формуле (2) имеем

9 − x2

x→3

= lim

3−ε dx

= lim arcsin

3−ε

= lim arcsin

3 −ε

−0 =

∫

0 9 − x2

ε→0

9 − x2

ε→0

интеграл сходится и его величина составляет

π.

Пример 7. Вычислить значение интеграла ∫ln x dx.

Решение. При x →0 функция ln x → −∞. По формуле (3) имеем

(xln x − x)

1ε = −1

(εln ε−ε)= −1−0 = −1,

∫ln x dx = lim

− lim

ε→0

ε→0 0+ε

ε→0

т.к.

= lim lnε

lim

ε lnε

= lim

= lim(−ε)= 0.

ε→0

ε→0 −

ε→0

ε2

Интеграл сходится и равен –1.

1 dx

Пример 8.

1 dx

= lim

−ε dx

= lim

−

= ∞ –

интеграл

∫

+ lim

−1

+ lim

ε→0

η→0∫

ε→0

η→0

−1 x

η x

расходится.

§ 5. Площади плоских фигур.

1 . Площадь в прямоугольных координатах. Если непрерывная

кривая задана в прямоугольных координатах

уравнением y = f (x)

[f (x)≥ 0],

то площадь криволинейной трапеции,

ограниченной этой

кривой, двумя вертикалями в точках

x = a

и x =b и отрезками оси

абсцисс a ≤ x ≤b (рис.2), определяется формулой

S = b∫ f (x)dx.

(1)

Пример

Вычислить

площадь,

ограниченную

параболой

y =

, прямыми

x =1 и x =3 и осью абсцисс (рис.3).

1 / 21 2 > Следующая >>>

Соседние файлы в папке 2020 Экзамен

#
09.06.20221.9 Mб0Глава I.doc
#
09.06.2022528.38 Кб4ДУ_ВЫС_ПОР.doc
#
09.06.202270.66 Кб0ЗАКЛЮЧЕНИЕ.doc
#
09.06.202227.14 Кб0Литература.doc
#
09.06.2022476.93 Кб0Обыкновенные дифференциальные уравнения.pdf
#
09.06.2022304.39 Кб1Определенные интегралы.pdf
#
09.06.2022330.75 Кб0Приложение 1.doc
#
09.06.20221.66 Mб0Рисунки.bmp
#
09.06.2022389.63 Кб0РЯДЫ.doc
#
09.06.202226.62 Кб0СОДЕРЖАНИЕ.doc
#
09.06.202250.69 Кб2Титул.doc