
2020 Экзамен / Обыкновенные дифференциальные уравнения
.pdf
Итого, общее решение: y = x(x + ln x +C).
C учетом начального условия y(1) = 0определяем постоянный коэффициент C.
0 =1+ ln1+C; C = −1.
Окончательно получаем: y = x2 + xln x − x.
Для проверки подставим полученный результат в исходное дифференциальное уравнение:
2x + ln x + x 1 −1− x −ln x +1 = x +1; |
верно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример. Найти общий интеграл уравнения x(y2 |
−1)dx + y(x2 −1)dy = 0 . |
|||||||||||||||||||||||||||||||||||||||||||
Это уравнение с разделяющимися переменными. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
xdx |
|
|
+ |
ydy |
|
= 0; |
|
|
|
|
∫ |
|
|
|
xdx |
|
= −∫ |
ydy |
; |
|||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
2 |
|
|
|
2 |
|
2 |
||||||||||||||||||||||||||||||
|
|
x −1 |
|
|
|
|
y −1 |
|
|
|
|
|
|
|
|
|
x −1 |
|
|
|
y −1 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
x2 −1 |
|
+ ln |
|
|
|
y2 −1 |
|
|
= ln C; |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общий интеграл имеет вид: |
(x2 −1)(y2 −1) = C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
С = 0,02 |
|
|
|
|
|
|
С = 0,5 |
С = 1 |
|
|
|
|
|
С = 2 |
||||||||||||||||||||||||||||||
Пример. Найти решение дифференциального уравнения, удовлетворяющее |
||||||||||||||||||||||||||||||||||||||||||||
заданным начальным условиям. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
y′cos x = (y +1)sin x; |
|
|
|
|
|
y(0) = 0. |
|
|||||||||||||||||||||||||||||||
Это уравнение с разделяющимися переменными. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y′ |
|
|
= |
|
|
sin x ; |
dy |
= tgxdx; |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y +1 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
dy |
|
|
|
|
|
|
|
|
|
cos x |
y +1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
∫ |
|
= |
|
∫tgxdx; |
|
|
|
ln |
|
y +1 |
|
= −ln |
|
cos x |
|
+ ln C; |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
y +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
ln |
|
(y +1)cos x |
|
= ln C; |
|
|
|
|
(y +1)cos x = C; |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Общее решение имеет вид: |
|
y = |
|
|
|
C |
|
|
−1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Найдем частное решение при заданном начальном условии у(0) = 0. |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 = С −1; |
|
|
C =1. |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Окончательно получаем: |
y = |
|
|
|
1 |
|
|
|
−1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Решить предыдущий пример другим способом.

Действительно, уравнение y′cos x = (y +1)sin x может быть рассмотрено как
линейное неоднородное дифференциальное уравнение. y′cos x − ysin x = sin x.
Решим соответствующее ему линейное однородное уравнение.
|
′ |
|
|
|
|
′ |
cos x = ysin x; |
dy |
= tgxdx; |
||||||
y cos x − ysin x = 0; |
|
|
y |
y |
|||||||||||
∫dy |
= ∫tgxdx + ln C; |
ln |
|
y |
|
= −ln |
|
cos x |
|
+ ln C; |
|
ycos x = C; |
|||
|
|
|
|
|
|||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
C |
. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
cos x |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение неоднородного уравнения будет иметь вид: y = cosC(xx) .
Тогда y′ = C′(x)cos x +2 C(x)sin x. cos x
Подставляя в исходное уравнение, получаем:
|
|
|
′ |
|
|
|
|
− C(x)sin x |
= sin x; |
|
|
|
[C (x)cos x +C(x)sin x] cos x |
||||||||
|
′ |
|
|
|
cos2 x |
|
|
cos x |
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
C (x)cos x |
= sin x; |
|
|
|
C(x) = ∫sin xdx = −cos x +C; |
||||
|
cos x |
|
|
C x) = sin x; |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
−cos x +C |
|
|
|
|
|
|
|
|
|
Итого y = |
; |
|
|
y = |
C |
−1; |
|
|
|
|
cos x |
|
|
cos x |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
С учетом начального условия у(0) = 0 получаем y = cos1 x −1;
Как видно результаты, полученные при решении данного дифференциального уравнения различными способами, совпадают.
При решении дифференциальных уравнений бывает возможно выбирать метод решения, исходя из сложности преобразований.
Пример. Решить уравнение y′+ ycos x = 12 sin 2x с начальным условием у(0) = 0.
Это линейное неоднородное уравнение. Решим соответствующее ему однородное уравнение.
′ |
+ ycos x = 0; |
dy |
= −cos xdx; |
ln |
|
y |
|
= −sin x +C1 |
; |
|
|
|
|||||||||
y |
y |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
y = e−sin x eC1 ; |
y = Ce−sin x ; |
|
|||||||
Для линейного неоднородного уравнения общее решение будет иметь вид: y = C(x)e−sin x ;
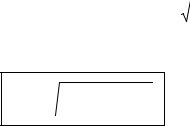
Для определения функции С(х) найдем производную функции у и подставим ее в исходное дифференциальное уравнение.
|
|
|
y |
′ |
= C |
′ |
|
|
|
−sin x |
−C |
(x)e |
−sin x |
cos x; |
|
||||||
|
|
|
|
(x)e |
|
|
|
|
|||||||||||||
′ |
|
−sin x |
−C |
(x)e |
−sin x |
cos x +C(x)e |
−sin x |
cos x = sin xcos x; |
|
||||||||||||
C (x)e |
|
|
|
|
|
|
|||||||||||||||
|
′ |
|
−sin x |
= sin xcos x; |
|
|
′ |
|
|
|
sin x |
sin xcos x; |
|
||||||||
|
C (x)e |
|
|
|
|
C (x) = e |
|
|
|
||||||||||||
|
|
|
|
|
|
sin x |
; |
|
|
dU = cos xdx; |
|
|
|||||||||
С(x) = ∫esin x sin xcos xdx |
V = e |
|
|
|
|
|
∫esin x cos xdx = |
||||||||||||||
= |
|
|
|
sin x |
|
|
|
|
|
|
|
|
= esin x sin x − |
||||||||
|
|
|
|
|
|
|
|
|
|
cos xdx; |
U |
|
|
|
|
|
|
||||
|
|
|
dV = e |
|
|
|
|
= sin x; |
|
||||||||||||
=esin x sin x −esin x +C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итого y = e−sin x (esin x sin x −esin x +C); |
|
|
|
|
|||||||||||||||||
|
y = sin x −1+Ce−sin x ; |
|
|
||||||||||||||||||
Проверим полученное общее решение подстановкой в исходное дифференциальное уравнение.
cos x +Ce−sin x (−cos x) +sin xcos x −cos x +Ce−sin x cos x = sin xcos x; (верно)
Найдем частное решение при у(0) = 0. |
|
||
|
0 = sin 0 −1+Ce0 ; |
C =1. |
|
|
|
|
|
Окончательно |
y = sin x + e−sin x −1. |
|
|
|
|
|
|
Пример. Найти решение дифференциального уравнения
20xdx −3ydy = 3x2 ydy −5xy2 dx
с начальным условием у(1) = 1.
Это уравнение может быть преобразовано и представлено как уравнение с разделенными переменными.
20x −3yy |
′ |
= 3x |
2 |
yy |
′ |
−5xy |
2 |
; |
|
|
|
′ |
|
2 |
+1) = 5x(y |
2 |
+ |
4); |
|||||||||||||||
|
|
|
|
|
3yy |
(x |
|
|
|||||||||||||||||||||||||
y′ |
|
|
3y |
|
|
|
|
|
5x |
|
|
|
|
|
|
|
3y |
|
dy |
|
5x |
|
|
|
|
||||||||
|
|
= |
|
|
; |
|
|
|
|
|
= |
|
|
dx; |
|
|
|
|
|||||||||||||||
y2 + 4 |
|
x2 +1 |
|
|
|
|
y2 + 4 |
x2 +1 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
∫ |
|
|
|
3y |
|
|
dy = ∫ |
|
5x |
|
|
dx; |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
y |
2 |
+ 4 |
|
x |
2 |
+1 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
3 ln(y2 |
+ 4) = |
|
5 ln(x2 |
+1) + ln C |
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(y2 + 4)3 = C (x2 +1)5 ; |
|
|
y2 + 4 = C 3 (x2 +1)2 ; |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 = C(x2 +1)3 − 4; |
|
|
|
|
|
|
|
|
|
||||||||||||||||
5
y = 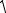 C(x2 +1)3 − 4;
C(x2 +1)3 − 4;
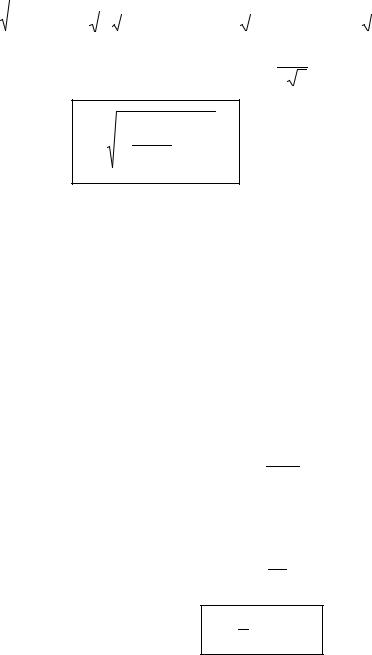
С учетом начального условия:
|
5 |
|
|
|
|
|
|
|
|
|
|
125 |
|
1 = С 23 |
− 4 = С3 |
|
− 4; 1 = 2C3 |
|
− 4; 5 = 2C3 |
|
|
; |
|||||
32 |
4 |
4; 125 = 8C3 4; C3 = |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
C = 2354 .
5
Окончательно y = 5 x2 +1 3 − 4.
2
Пример. Решить дифференциальное уравнение xy′+ y = x +1 с начальным условием у(1) = 0.
Это линейное неоднородное уравнение.
Решим соответствующее ему однородное уравнение.
|
′ |
|
xdy |
dy |
dx |
|
|
|
|
|
xy |
+ y = 0; |
dx = −y; |
y = − x ; |
ln |
y |
= −ln |
x |
+ ln C; |
||
|
|
|
|
|
|
|
|
|||
|
|
|
xy = C; |
|
y = C |
; |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
Решение неоднородного уравнения будет иметь вид:
y = C(xx) ;
Подставим в исходное уравнение:
|
′ |
|
C(x) |
|
′ |
|
′ |
x |
C (x)x −C(x) |
+ |
= x +1; |
C (x)x |
= x +1; |
||
x2 |
x |
x |
C (x) = x +1; |
C(x) = x2 + x +C; 2
Общее решение будет иметь вид: y = 2x +1+ Cx ;
C учетом начального условия у(1) = 0: |
|
0 = 1 |
+1+C; |
C = − 3 ; |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Частное решение: |
y = |
x |
− |
3 |
+1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример. Найти решение дифференциального уравнения xy′ = yln |
|
|
с начальным |
|||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
условием у(1) = е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Это уравнение может быть приведено к виду уравнения с разделяющимися |
||||||||||||||||||||||||||||||
переменными с помощью замены переменных. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
y |
|
|
|
|
y |
|
|
u |
|
|
|
u |
|
|
′ |
|
′ |
u |
|
u |
|
|
|
|
||||
Обозначим: ln |
|
|
= u; |
|
|
|
|
= e |
|
; |
y = xe |
|
; |
y |
|
|
+ e |
|
; |
|
|
|
||||||||
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Уравнение принимает вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
′ u |
+ e |
u |
= e |
u |
u; |
|
xu |
′ |
+1 = u; |
xu |
′ |
= u − |
1; |
|
|
|
|
|
|||||||
|
|
xu e |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Получили уравнение с разделяющимися переменными.
|
|
|
|
|
|
|
x du |
= u −1; |
|
|
|
du |
|
|
= dx |
; |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
u −1 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
du |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||
|
|
∫ |
= ∫dx; |
ln |
|
u −1 |
|
= ln |
|
x |
|
+ ln C; |
|
u −1 = Cx; |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
u −1 |
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
y |
|
|
|
||||||||||||||
Сделаем обратную замену: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cx+1 |
|
||||||||||||||||||
Cx = ln |
|
|
|
−1; |
ln |
|
|
|
|
= Cx |
+1; |
|
|
= e |
|
; |
||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общее решение: |
y = xeCx+1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
C учетом начального условия у(1) = е: |
|
|
|
e = eC+1; |
|
C = 0; |
|
|
|
|
|
|||||||||||||||||||||||||||
Частное решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = ex; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Второй способ решения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xy |
= yln x |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
xy′ = yln y − yln x; |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
y′− |
y |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
ln y = − |
|
ln x; |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
||||||||||||||||||||||||
Получили линейноенеоднородноедифференциальное уравнение. Соответствующее однородное:
|
|
|
|
|
|
|
y′− |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
ln y = 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
∫d(ln y) |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
y′ = |
|
y |
ln y; |
|
|
|
|
dy |
|
= dx |
; |
|
= ∫dx |
; |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yln y |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
ln y |
|
|
x |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
ln |
|
ln y |
|
= ln |
|
x |
|
+ ln C; |
|
|
|
ln y = Cx; |
|
|
|
y = eCx ; |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
Решение исходного уравнения ищем в виде: y = eC ( x) x ; |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Тогда |
y |
′ |
= e |
C ( x) x |
(C |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x)x +C(x)); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Подставим полученные результаты в исходное уравнение: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C ( x) x |
|
|
′ |
|
|
|
|
|
|
|
|
C ( x) x |
|
eC ( x) x |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
xe |
|
|
|
|
(C (x)x +C(x)) |
= e |
|
|
|
ln |
|
x ; |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
C |
(x) + xC(x) = C(x)x −ln x; |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
′ |
|
|
|
|
|
|
|
′ |
|
|
|
|
ln x |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
= −ln x; |
|
|
|
|
|
|
|
|
x2 |
; |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
(x) |
|
|
|
C (x) = − |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
C(x) = −∫ |
ln x |
|
u = ln x; |
|
dv |
= |
x |
2 |
; |
|
|
|
ln x |
− ∫ |
− dx |
= |
ln x |
+ |
1 |
+C; |
||||||||||||||||||||||
|
|
|
x |
2 dx = |
|
|
|
|
dx |
|
|
|
|
|
= − − |
|
x |
|
x |
2 |
|
x |
x |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; v = − |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
du = |
|
|
x |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = eC( x) x = eln x+1+Cx = xeCx+1; |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получаем общее решение: |
y = xeCx+1; |
|
|
|
|
|
|||||||||||||||||||||||
Пример. Решить дифференциальное уравнение |
|
y |
′ |
+ e |
y |
|
|
y |
|
= 0 |
с начальным |
|||||||||||||||||||||||||||||||||
|
x |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
− x |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
условием у(1)=0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В этом уравнении также удобно применить замену переменных. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
y |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
xu′ |
|
|
|
||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
e |
= u; |
|
x |
= ln u; |
|
|
y = xln u; |
|
|
y |
= ln u + u ; |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Уравнение принимает вид: ln u + |
xu |
′ |
+u −ln u = 0; |
|
xu |
′ |
+u |
2 |
|
= 0; |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
u |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
xu′ = −u2 ; |
|
|
|
|
|
du2 = |
− dx ; |
|
|
|
|
∫du2 = −∫dx; |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
u |
|
|
x |
1 |
|
u |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
= ln |
|
x |
|
+ ln C; |
= ln Cx; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
u |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Делаем обратную подстановку: e− |
= ln Cx; |
|
|
− |
y |
|
= ln(lnCx); |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Общее решение: |
y = −xln(lnCx); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
C учетом начального условия у(1) = 0: |
|
|
0 = −ln(lnC); |
|
C = e; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Частное решение: |
y = −xln(ln ex); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Второй способ решения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
′ |
+ e |
y |
|
y |
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Замена переменной: |
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
u = x ; |
y = ux; |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
= u x +u; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
u′x +u + eu −u = 0
u′x + eu = 0 dudx x = −eu
−e−u du = dxx
−∫e−u du = ∫dxx ;
|
e−u = ln |
|
x |
|
+ ln C; |
e−u = ln |
|
Cx |
|
; |
|||||||||
|
|
|
|
|
|||||||||||||||
|
−u = ln(ln |
|
Cx |
|
); |
u = −ln(ln |
|
Cx |
|
); |
|||||||||
|
|
|
|
|
|||||||||||||||
Общее решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = −xln(lnCx); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
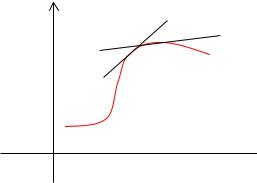
Геометрическая интерпретация решений дифференциальных уравнений первого порядка.
у |
a |
b
A S
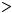 x
x
Как уже говорилось выше (см. Интегральные кривые. ), линия S, которая задается функцией, являющейся какимлибо решением дифференциального уравнения, называется интегральной кривой уравнения y′ = f (x, y).
Производная y’ является угловым коэффициентом касательной к интегральной
кривой.
В любой точке А(х, у) интегральной кривой этот угловой коэффициент касательной может быть найден еще до решения дифференциального уравнения.
Т.к. касательная указывает направление интегральной кривой еще до ее непосредственного построения, то при условии непрерывности функции f(x, y) и непрерывного перемещения точки А можно наглядно изобразить поле направлений кривых, которые получаются в результате интегрирования дифференциального уравнения, т.е. представляют собой его общее решение.
Определение. Множество касательных в каждой точке рассматриваемой области называется полем направлений.
С учетом сказанного выше можно привести следующее геометрическое истолкование дифференциального уравнения:
1)Задать дифференциальное уравнение первого порядка – это значит задать поле направлений.
2)Решить или проинтегрировать дифференциальное уравнение – это значит найти всевозможные кривые, у которых направление касательных в каждой точке совпадает с полем направлений.
Определение. Линии равного наклона в поле направлений называются
изоклинами.
Дифференциальные уравнения высших порядков.
Определение. Дифференциальным уравнением порядка n называется уравнение
вида:
F (x, y, y′,..., y(n) ) = 0
В некоторых случаях это уравнение можно разрешить относительно y(n): y(n) = f (x, y, y′,..., y(n−1) ).
Так же как и уравнение первого порядка, уравнения высших порядков имеют бесконечное количество решений.

Определение. |
Решение |
|
y = ϕ(x) удовлетворяет |
начальным |
условиям |
|||
x0 , y0 , y0′,..., y0(n−1) , если ϕ(x0 ) = y0 , |
ϕ′(x0 ) = y0′, .... |
, ϕ(n−1) (x0 ) = y0(n−1) . |
|
|
|
|||
Определение. |
Нахождение |
решения |
уравнения |
F (x, y, y ,..., y |
|
) = 0, |
||
|
|
|
|
|
′ |
|
(n) |
|
удовлетворяющего начальным условиям x0 , y0 , y0′,..., y0(n−1) , называется решением задачи
Коши.
Теорема Коши. (Теорема о необходимых и достаточных условиях существования решения задачи Коши).
Еслифункция(n-1) –йпеременныхвида f (x, y, y′,..., y(n−1) ) внекоторойобластиD (n- 1)- мерного пространства непрерывна и имеет непрерывные частные производные по y, y′,..., y(n−1) , то какова бы не была точка (x0 , y0 , y0′,..., y0(n−1) ) в этой области, существует
единственное решение y = ϕ(x) уравнения y(n) = f (x, y, y′,..., y(n−1) ) , определенного в некотором интервале, содержащем точку х0, удовлетворяющее начальным условиям
x0 , y0 , y0′,..., y0(n−1) .
Дифференциальные уравнения высших порядков, решение которых может быть найдено аналитически, можно разделить на несколько основных типов.
Рассмотрим подробнее методы нахождения решений этих уравнений.
Уравнения, допускающие понижение порядка.
Понижение порядка дифференциального уравнения – основной метод решения уравнений высших порядков. Этот метод дает возможность сравнительно легко находить решение, однако, он применим далеко не ко всем уравнениям. Рассмотрим случаи, когда возможно понижение порядка.
Уравнения вида y(n) = f(x).
Если f(x) – функция непрерывная на некотором промежутке a < x < b, то решение может быть найдено последовательным интегрированием.
y(n−1) = ∫ f (x)dx +C1;
y(n−2) = ∫(∫ f (x)dx +C1 )dx +C2 = ∫dx∫ f (x)dx +C1 x +C2 ;
…………………………………………………………….
|
|
y = ∫dx∫dx....∫ |
f (x)dx +C1 |
xn−1 |
|
|
|
+C2 |
xn−2 |
|
|
+... +Cn ; |
|
|
|||||||||
|
|
(n −1)! |
(n − 2)! |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример. |
|
Решить уравнение y′′′ = e2x с начальными условиями x0 = |
|
0; y0 = 1; |
|||||||||||||||||||
|
|
||||||||||||||||||||||
y0′ = −1; y0′′ = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
y′′ = ∫e2xdx +C1 |
= |
1 e2x +C1; |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
y′ = |
∫ |
|
1 |
e |
2x |
+C |
|
|
|
1 |
e |
2x |
+C x +C |
|
|
; |
|
|
|||
|
|
|
2 |
|
dx = |
4 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|||||
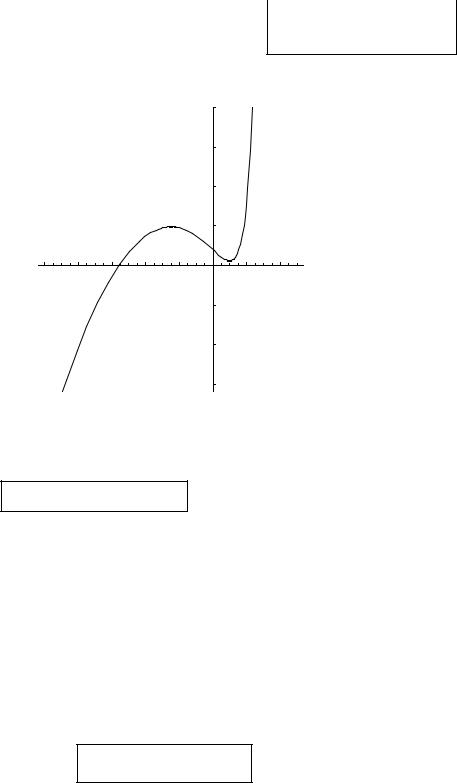
y = ∫ 14 e2x +C1 x +C2 = 18 e2x + 12 C1 x2 +C2 x +C3 ;
Подставим начальные условия:
1 = |
1 +С |
; −1 = |
1 +C |
2 |
; 0 |
= |
1 +C |
; |
||||||
|
8 |
3 |
|
|
|
4 |
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
C |
= − 1 ; |
C |
2 |
= − 5 ; C |
3 |
= 7 ; |
|
|
|||||
|
1 |
2 |
|
4 |
|
|
|
8 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Получаем частное решение (решение задачи Коши): y = 18 e2x − 14 x2 − 54 x + 78 .
Ниже показана интегральная кривая данного дифференциального уравнения.
10
7.5
5
2.5
-10 |
-8 |
-6 |
-4 |
-2 |
2 |
4 |
-2.5
-5
-7.5
Уравнения, не содержащие явно искомой функции и ее производных до порядка k – 1 включительно.
Это уравнения вида: F (x, y(k) , y(k+1) ,..., y(n) ) = 0.
В уравнениях такого типа возможно понижение порядка на k единиц. Для этого производят замену переменной:
|
y |
(k) |
= z; y |
(k+1) |
′ |
y |
(n) |
= z |
(n−k) |
. |
|
|
|
|
= z ; ... |
|
|
||||||
Тогда получаем: |
′ |
|
(n−k) |
) = 0. |
|
|
|
|
|
|
|
F (x, z, z ,..., z |
|
|
|
|
|
|
|
||||
Теперь допустим, что полученное дифференциальное уравнение проинтегрировано и совокупность его решений выражается соотношением:
z = ψ(x,C1 ,C2 ,...,Cn−k ).
Делая обратную подстановку, имеем:
y(k) = ψ(x,C1 ,C2 ,...,Cn−k )
Интегрируя полученное соотношение последовательно k раз, получаем окончательный ответ:
y = ϕ(x,C1 ,C2 ,...,Cn ).

Пример. Найти общее решение уравнения y′′′ = |
|
y′′ |
. |
|
|
|
||||||||||||||||||||
|
x |
|
|
|
||||||||||||||||||||||
Применяем подстановку |
|
|
′′ |
|
z |
′ |
|
|
|
|
′′′ |
|
|
|
|
|
|
|
|
|
|
|
||||
z = y ; |
|
|
= y ; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
z′ = |
|
z |
; |
|
dz |
= |
z |
; |
|
|
dz |
= dx |
; |
|
|
|
|
∫dz |
= ∫dx |
; |
||||||
|
|
|
dx |
|
|
|
z |
|
|
|
||||||||||||||||
|
|
x |
|
|
x |
x |
|
|
|
|
|
|
z |
x |
|
|||||||||||
|
|
|
ln |
|
z |
|
= ln |
|
x |
|
+ ln C1; |
z = C1 x; |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Произведя обратную замену, получаем: |
|
|
|
C1 |
|
|
|
|
|
|||||||||||||||||
|
|
y′′ = C1 x; |
|
|
|
|
|
y′ = ∫C1 xdx = |
x2 |
+C2 ; |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
y = ∫ C21 x2 +C2 dx = C61 x3 +C2 x +C3 ;
Общее решение исходного дифференциального уравнения: y = Cx3 +C2 x +C3 ;
Отметим, что это соотношение является решением для всех значений переменной х кроме значения х =0.
Уравнения, не содержащие явно независимой переменной.
Это уравнения вида F (y, y′,..., y(n) ) = 0.
Порядоктаких уравненийможетбытьпониженнаединицуспомощьюзаменыпеременных
y′ = p. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′′ = |
dy′ |
|
|
|
dy′ |
dy |
|
dp |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
= |
|
|
dx |
= |
dy p; |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
dx |
|
dy |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dp |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dy′′ |
|
dy′′ |
|
dy |
|
dy′′ |
|
|
|
d |
p |
|
|
d |
2 |
p |
|
|
dp |
2 |
|||||
y′′′ = |
|
|
|
p = |
|
|
dy |
|
p |
|
|
p |
2 |
p; и т.д. |
||||||||||||
|
= |
|
|
|
= |
|
|
|
|
|
|
|
|
= |
|
|
2 |
|
+ |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
dx |
|
dy |
|
dx |
|
dy |
|
|
|
|
|
dy |
|
|
|
|
dy |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|||||||||
Подставляя эти значения в исходное дифференциальное уравнение, получаем:
|
dp |
|
d |
n−1 |
p |
|
|
|
|
,..., |
|
|
|
= 0 |
|||
F1 y, p, |
dy |
dy |
n−1 |
|
||||
|
|
|
|
|
|
|||
Если это уравнение проинтегрировать, |
и |
Ф(y, p,C1 ,C2 ,...,Cn−1 ) = 0 - совокупность |
||||||
его решений, то для решения данного дифференциального уравнения остается решить уравнение первого порядка:
Ф(y, y′,C1 ,C2 ,...,Cn−1 ) = 0.
Пример. Найти общее решение уравнения yy′′−(y′)2 − 4yy′ = 0.
Замена переменной: |
′ |
y |
′′ |
|
dp |
|
|
|
p = y ; |
|
= dy p; |
|
− p − 4y |
= 0; |
|||
yp dp − p2 − 4yp = 0; |
p y dp |
|||||||
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
||
