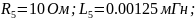- •1. Текст задания 8
- •Задание 1
- •1. Текст задания
- •2. Вариант
- •3. Выполнение задания
- •4. Заключение
- •Задание 2
- •1. Текст задания
- •2. Вариант
- •3. Выполнение задания
- •4. Ответы на вопросы
- •Вопрос 1. Как располагаются на комплексной плоскости корни хп при
- •Вопрос 2. Чему равна высота пика лачх?
- •5. Заключение
- •Заключение
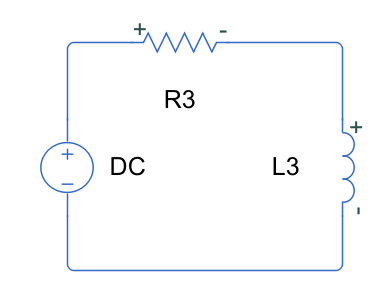
Прямоугольный импульс (Signal Generator) с амплитудным значением final value = , где n – номер варианта. (не менее 3 прямоугольных импульсов за все время симуляции.)
Получить переходные характеристики для каждой из построенных моделей при различных входных сигналах. Выполнить сравнительный анализ.
Построить ПФ объекта в MATLAB (Command Window) и получить следующие характеристики:
- Переходная характеристика;
- Логарифмические частотные характеристики;
- Амплитудно-фазовая характеристика;
- Расположение корней объекта на корневой плоскости.
Проанализировать полученные характеристики.
2. Вариант
№ варианта |
Схема |
Значения |
5 |
|
|
Таблица 1. Условие первого задания
3. Выполнение задания
Математическая модель (ММ)
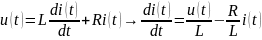
Переход к передаточной функции
Применяем оператор дифференцирования, а затем - прямое преобразование Лапласа


Тогда по определению ПФ примет следующий вид:

Построение компьютерных моделей
В качестве входного сигнала используем:
Ступенчатый импульс (Step) со значением final value =
 В
ВПрямоугольный импульс (Signal Generator) с амплитудным значением Amplitude = В.
Модели на основе ДУ и ПФ в среде Simulink показаны на рисунках 1 и 2.
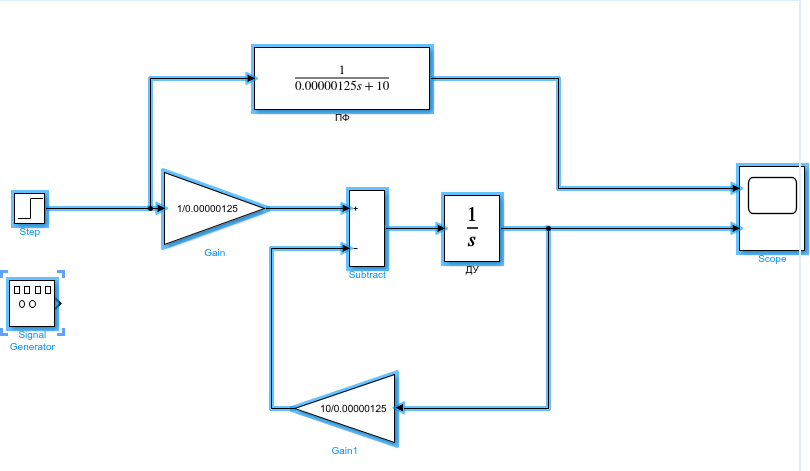
Рисунок 1 – Модель с блоком step
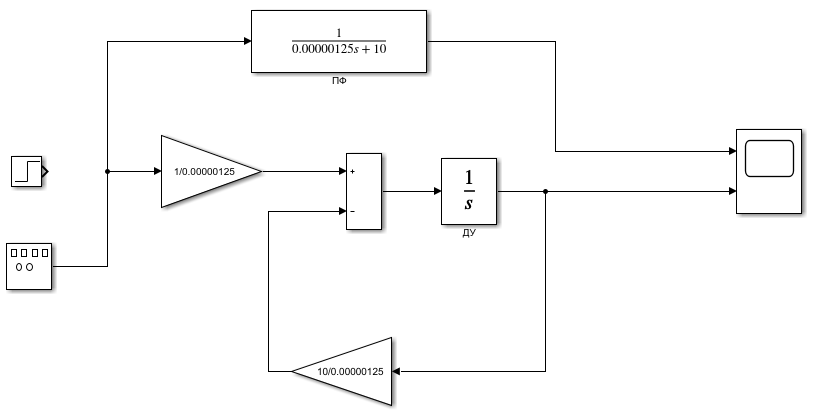
Рисунок 2 – Модель с блоком Signal Generator
Получение переходных характеристик при различных входных сигналах.
Рассмотрены переходная характеристика для моделей на основе ПФ и ДУ со ступенчатым импульсом (Рис. 3) и переходная характеристика для моделей на основе ПФ и ДУ с прямоугольным импульсом (Рис. 4).
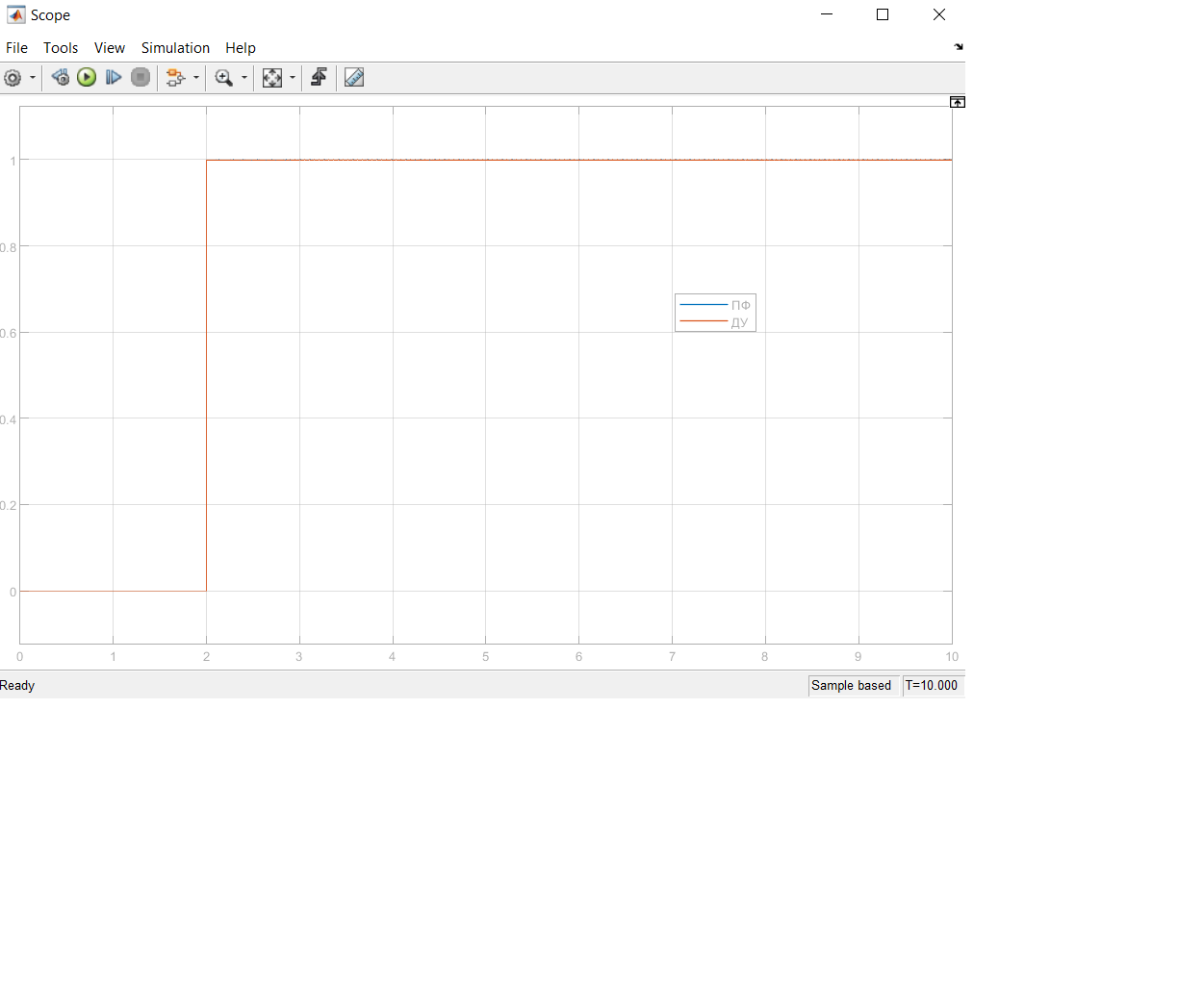
Рисунок 3 – Переходная характеристика при ступенчатом импульсе для W(s)
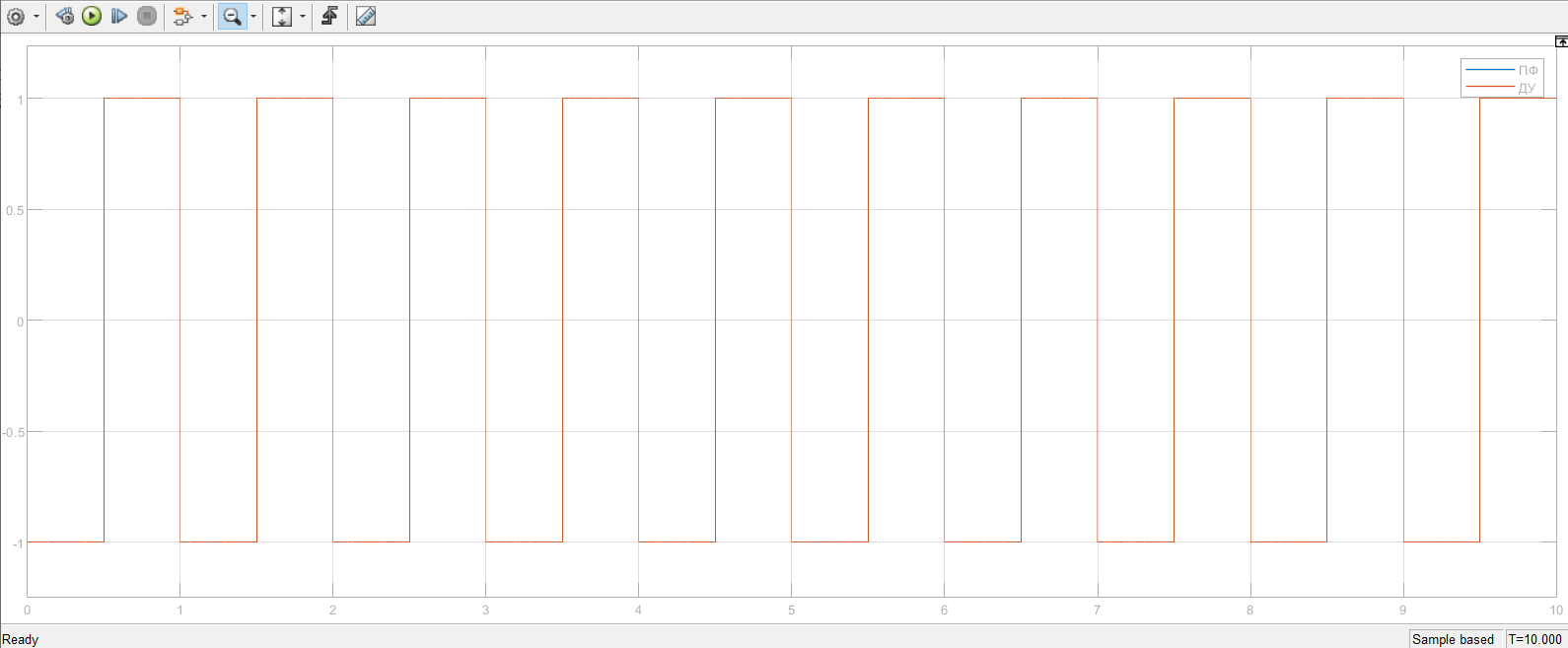
Рисунок 4 – Переходная характеристика при прямоугольном импульсе для W(s)
Графики переходных характеристик моделей, построенных на основе ПФ и ДУ, совпадают для разных входных сигналов. Это свидетельствует об эквивалентности моделей
Построение ПФ объекта в MATLAB
В MATLAB (Command Window) была построена ПФ объекта и получены ПХ, ЛЧХ, АФХ, расположение корней объекта на корневой плоскости (Рис. 5).
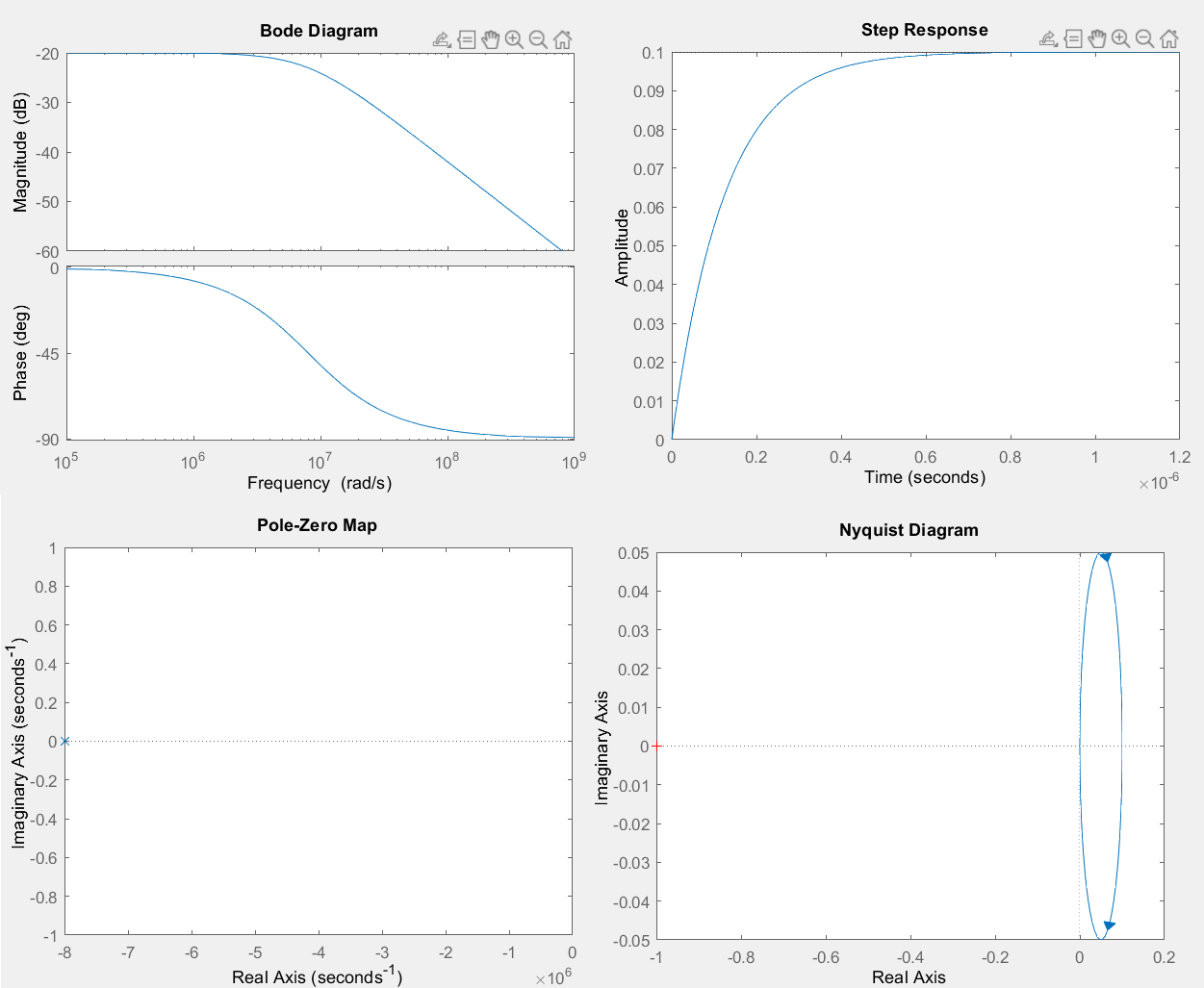 Рисунок
5 – смоделированные графики
Bode
Diagram
– ЛЧХ, Step
Response
– ПХ, Polo-Zero
Map
– расположение корней характеристического
полинома, Nyquist
Diagram
– АФХ
Рисунок
5 – смоделированные графики
Bode
Diagram
– ЛЧХ, Step
Response
– ПХ, Polo-Zero
Map
– расположение корней характеристического
полинома, Nyquist
Diagram
– АФХ
4. Заключение
В ходе выполнения первого задания была составлена ММ в ДУ для RL-цепи, а затем был осуществлен переход от ММ в ДУ к ПФ. В среде MATLAB/Simulink были получены переходные характеристики для каждой из построенных моделей при различных входных сигналах (ступенчатый и прямоугольный). В результате сравнительного анализа графиков подтверждена эквивалентность моделей. В MATLAB была построена ПФ объекта и получены переходная характеристика, логарифмические частотные характеристики, амплитудно-фазовая характеристика и карта нулей и полюсов ПФ.
Задание 2
1. Текст задания
Для звена вида:
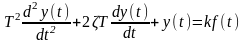
определить
переходную и частотные характеристики
(АФХ и ЛЧХ) при выбранных значениях (см.
варианты задания) параметров
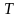 ,
,
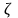 ,
привести графики.
,
привести графики.
Провести исследование характеристик звена, состоящее в следующем.
Проанализировать движение корней (траекторий корней) ХП на комплексной плоскости при изменении параметра , привести графики.
Построить график зависимости резонансного пика АЧХ от коэффициента демпфирования в пределах
 .
.Построить график зависимости резонансной частоты
 от постоянной времени
при выбранном значении
.
от постоянной времени
при выбранном значении
.Определить экспериментально оптимальное значение коэффициента демпфирования
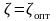 из условия минимума времени
из условия минимума времени
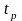 затухания процесса (принять за
время, начиная с которого переходная
характеристика остается в пределах
5% от установившегося значения). Как
располагаются на комплексной плоскости
корни ХП при
?
Чему равна высота пика ЛАЧХ?
затухания процесса (принять за
время, начиная с которого переходная
характеристика остается в пределах
5% от установившегося значения). Как
располагаются на комплексной плоскости
корни ХП при
?
Чему равна высота пика ЛАЧХ?Определить переходную и частотные характеристики (АФХ и ЛЧХ) при изменении знака коэффициента демпфирования на
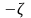 ,
привести графики.
,
привести графики.
2. Вариант
Вариант: n = 5
k=10, T=5, ξ=0.4
3. Выполнение задания
3.1. Определение
переходной и частотных (АФХ и ЛЧХ)
характеристик (Рис.6) при выбранных по
варианту значениях параметров
=5,
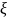 =0.4 было осуществлено при помощи
программных средств MATLAB (Command Window),
представленных в программе 1.
=0.4 было осуществлено при помощи
программных средств MATLAB (Command Window),
представленных в программе 1.
k = 10;
T = 5;
Z = 0.4;
W = tf([k], [T*T, 2*Z*T, 1]);
figure(1);
subplot(1,3,1);
step(W); %Переходная характеристика
subplot(1,3,2);
bode(W); % ЛАЧХ и ЛФЧХ
subplot(1,3,3);
nyquist(W); %АФХ
grid on;
Программа 1 – Определение ПХ, АФХ и ЛЧХ
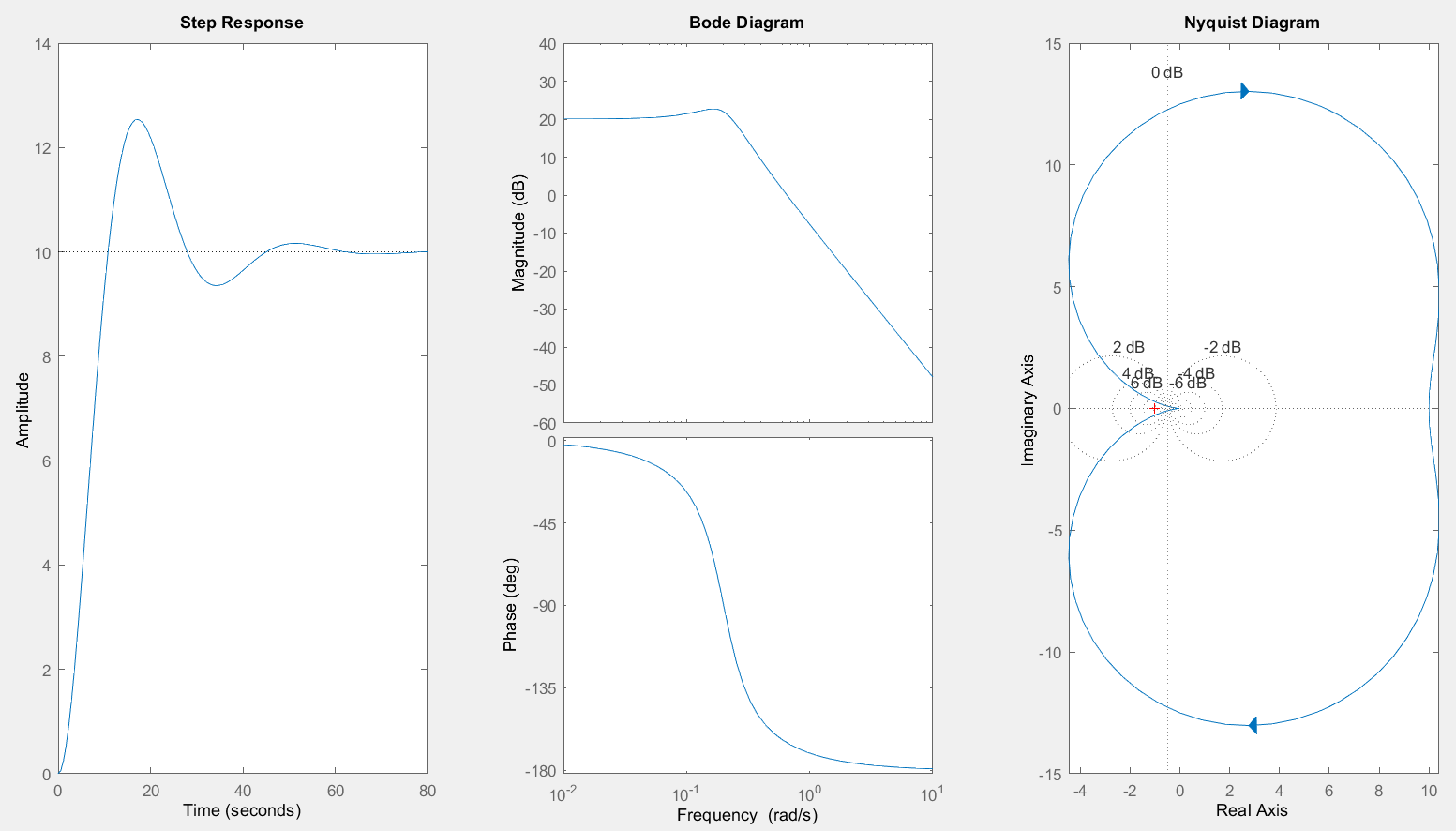 Рисунок
6 – ПХ, ЛЧХ, АФХ при заданных параметрах
3.2.
Анализ траекторий корней ХП на комплексной
плоскости при изменении параметра
(Рис.7) был осуществлен при помощи
программных средств MATLAB (Command Window),
представленных в программе 2.
Рисунок
6 – ПХ, ЛЧХ, АФХ при заданных параметрах
3.2.
Анализ траекторий корней ХП на комплексной
плоскости при изменении параметра
(Рис.7) был осуществлен при помощи
программных средств MATLAB (Command Window),
представленных в программе 2.
k = 10;
T = 5;
figure(2);
sgrid;
for ZNew = 0.0 : 0.01 : 1.0
hold on;
pzmap(tf(k, [T^2 2*ZNew*T 1]));
end
Программа 2 –Движение корней ПФ при изменении параметра Z
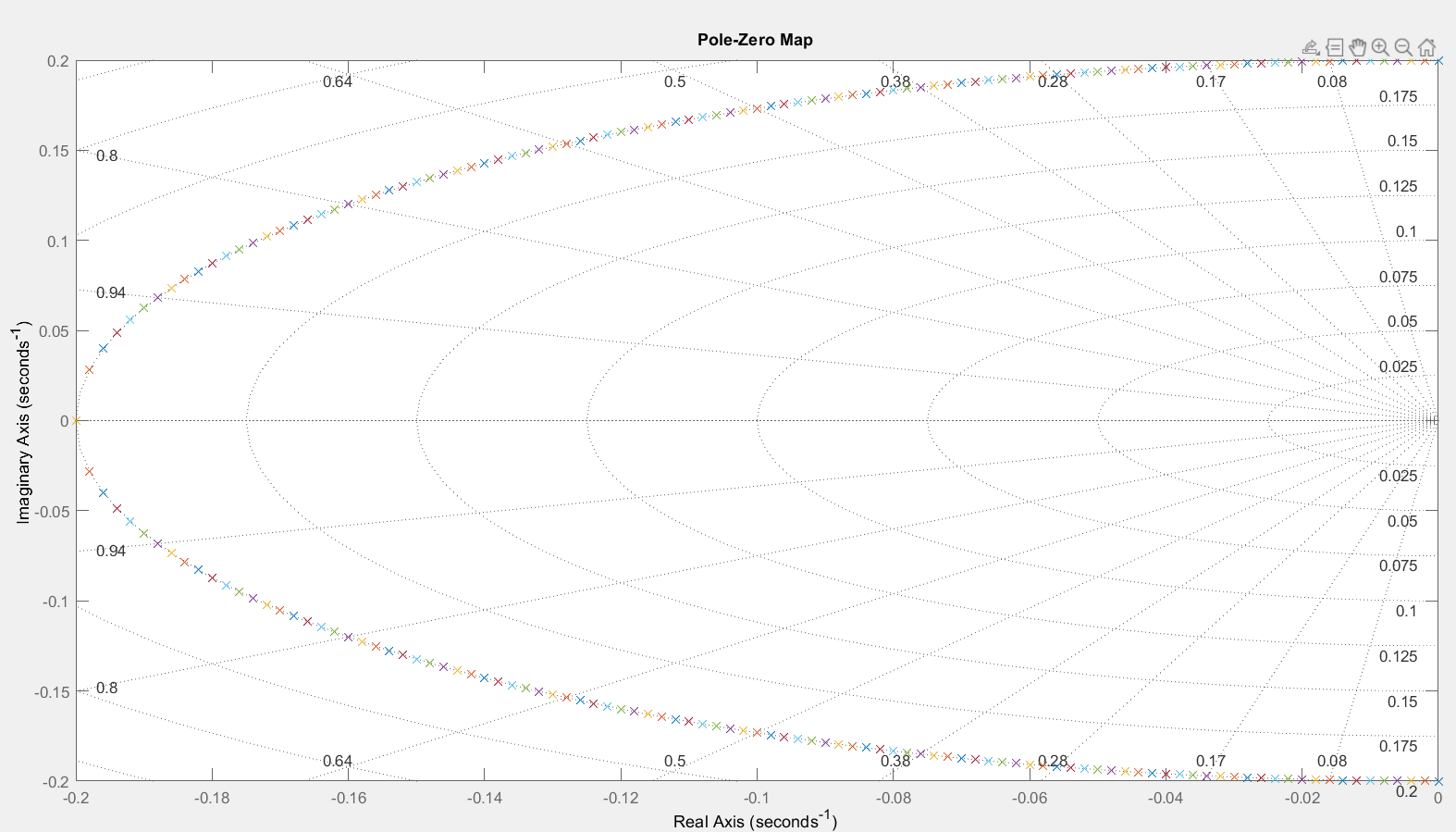 Рисунок 7 – Движение
корней ПФ на комплексной плоскости при
0≤𝜉≤1
Рисунок 7 – Движение
корней ПФ на комплексной плоскости при
0≤𝜉≤1
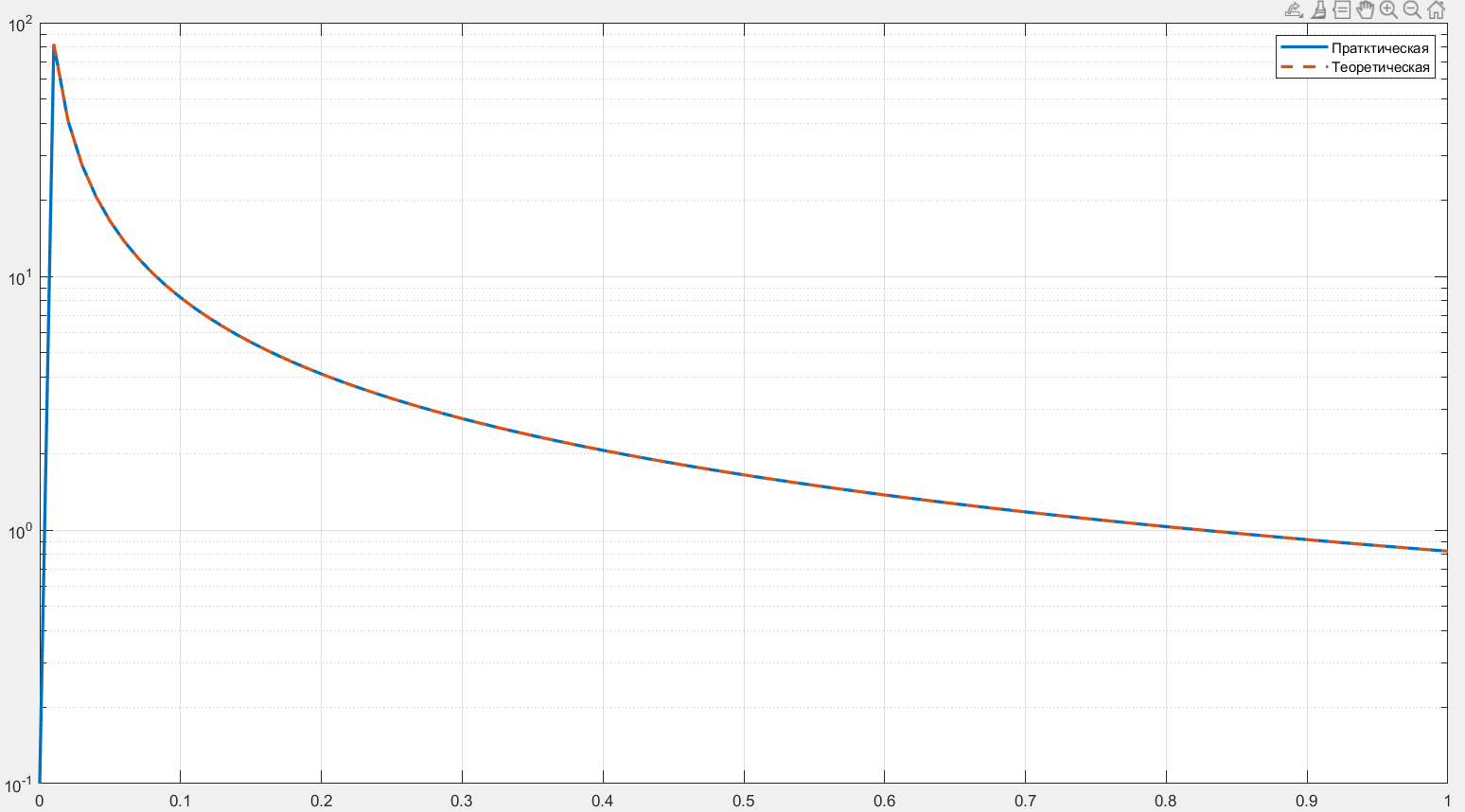
3.3. График зависимости резонансного пика АЧХ от коэффициента демпфирования в пределах (Рис.8) был построен при помощи программных средств MATLAB (Command Window), представленных в программе 3.
k = 10;
T = 5;
R = zeros(1, 101);
Rt = zeros(1, 101);
Z = zeros(1, 101);
for ZNew = 0.00 : 0.01 :1.0
[mag, phase, wout] = bode(tf(k, [T^2 2*ZNew*T 1]));
R(1, int8(ZNew*100+1)) = max(mag(1,1,:));
Rt(1, int8(ZNew*100+1)) = k/(2*ZNew*sqrt(1-ZNew^2));
Z(1,int8(ZNew*100+1)) = ZNew;
end
figure(3);
semilogy(Z, R, '-', Z, Rt, '--', 'LineWidth', 2);
legend('Практическая', 'Теоретическая');
grid on;
Программа 3 – Зависимость резонансного пика АЧХ от параметра Z
График теоретической зависимости строился по формуле:
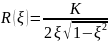
 Рисунок
8 – График зависимости резонансного
пика от коэффициента демпфирования
Рисунок
8 – График зависимости резонансного
пика от коэффициента демпфирования
Расхождение теоретической и практической зависимостей при значениях 𝜉 ≥ 0.7 связано с тем, что при таких коэффициентах не наблюдается резонансного пика.
3.4. График зависимости резонансной частоты от постоянной времени при выбранном значении (Рис.9) был построен при помощи программных средств MATLAB (Command Window), представленных в программе 4.
k = 10;
Z = 0.4;
w = zeros(1, 101);
wt = zeros(1, 101);
t = zeros(1, 101);
for TEx = 0.00 : 0.01 : 1.0
[mag, phase, wout] = bode(tf(k, [TEx^2 2*Z*TEx 1]));
[Rmax, ind] = max(mag(1,1,:));
w(1, int8(TEx*100+1)) = wout(ind);
wt(1, int8(TEx*100+1)) = sqrt(1-2*Z^2)/TEx;
t(1,int8(TEx*100+1)) = TEx;
end
figure(4);
semilogy(t, w, '-', t, wt, '--', 'LineWidth', 2);
legend('Практическая', 'Теоретическая');
grid on;
Программа 4 –Зависимость резонансной частоты от параметра T
График теоретической зависимости строился по формуле:
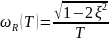
 Рисунок
9 – График зависимости резонансной
частоты
от постоянной времени
при выбранном значении
3.5.
Оптимальное значение коэффициента
демпфирования
было определено экспериментальным
путем из условия минимума времени
затухания процесса при помощи программных
средств MATLAB (Command Window), представленных
в программе 5. Также
была рассчитана высота пика ЛАЧХ при
Рисунок
9 – График зависимости резонансной
частоты
от постоянной времени
при выбранном значении
3.5.
Оптимальное значение коэффициента
демпфирования
было определено экспериментальным
путем из условия минимума времени
затухания процесса при помощи программных
средств MATLAB (Command Window), представленных
в программе 5. Также
была рассчитана высота пика ЛАЧХ при
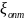 :
:
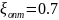
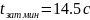
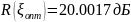
График
расположения корней ПФ при
 приведен на рисунке 10.
приведен на рисунке 10.
k = 10;
T = 5;
t_p = zeros(1, 101);
for ZEx = 0.0 : 0.01 : 1.0
[y, t] = step(tf(k, [T^2 2*ZEx*T 1]), (0.0 : 0.01 : 100.0));
i = length(y);
Y = y(i); i = i-1;
while y(i)>= Y*0.95 && y(i)<=Y*1.05
i = i-1;
end
t_p(1, int8(ZEx*100+1)) = t(i+1);
end
[t_min, ind] = min(t_p);
Z_opt = (ind-1)/100
t_min
figure(5)
pzmap(tf(k, [T^2 2*Z_opt*T 1]));
grid on;
[mag, phase, wout] = bode(tf(k, [T^2 2*Z_opt*T 1]));
R_opt = 20*log10(max(mag(1,1,:)))
Программа 5 – Экспериментальное определение оптимального значения коэффициента демпфирования
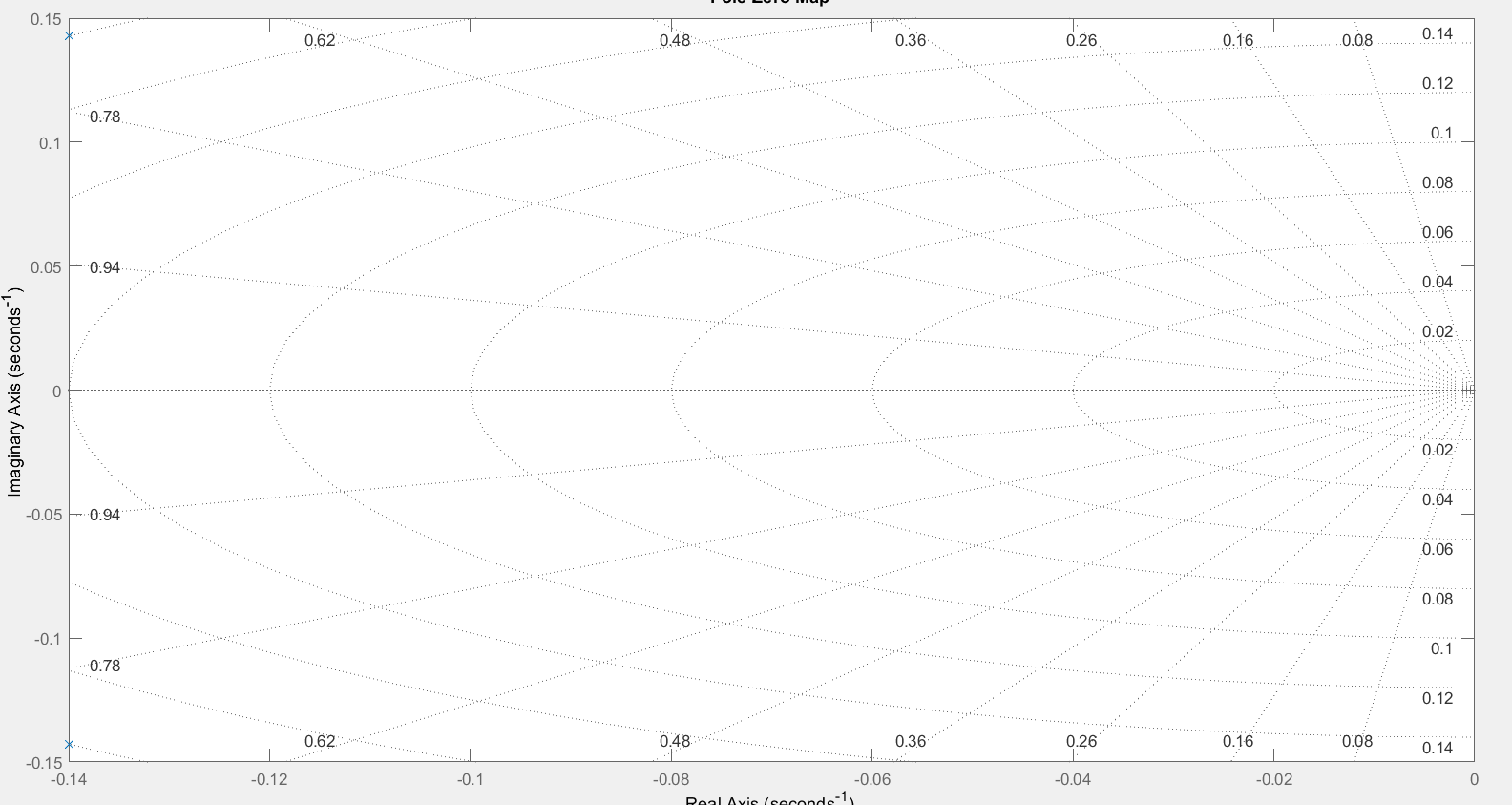 Рисунок
10 – График расположения
корней ПФ при
Рисунок
10 – График расположения
корней ПФ при
3.6. Переходная и
частотные характеристики (АФХ и ЛЧХ)
были определены при изменении знака
коэффициента демпфирования
на
 (Рис.11) при помощи программных средств
MATLAB (Command Window), представленных в программе
6.
(Рис.11) при помощи программных средств
MATLAB (Command Window), представленных в программе
6.
k = 10;
T = 5;
Xi = 0.4;
minusXi = -Xi;
W = tf(k, [T^2 2*minusXi*T 1]);
figure(6);
subplot(1,3,1);
step(W);
subplot(1,3,2);
bode(W);
subplot(1,3,3);
nyquist(W);
grid on;
Программа 6 – Получение ПХ, АФХ и ЛЧХ при изменении знака коэффициента демпфирования
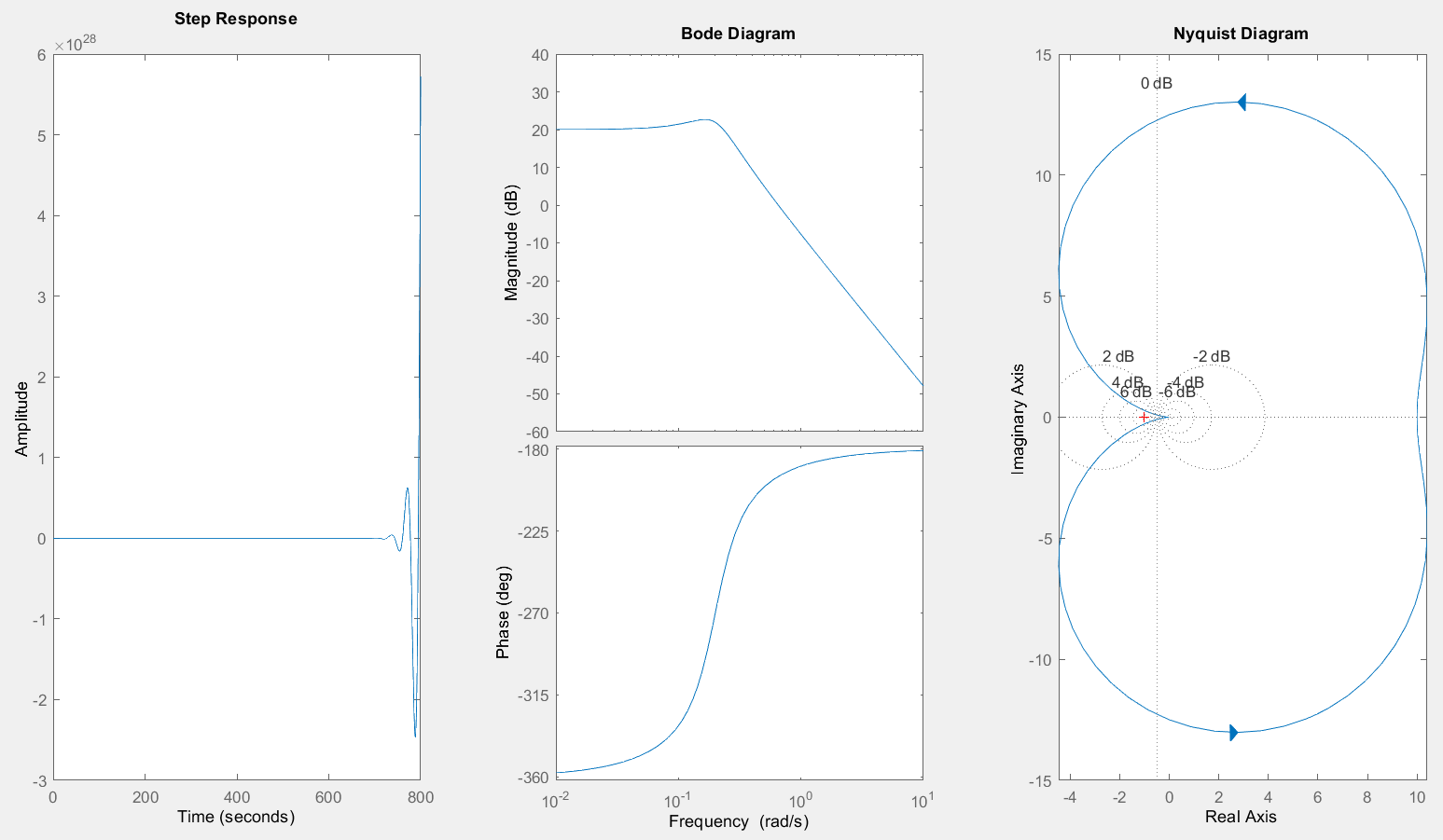 Рисунок 11 –
График ПХ, АФХ и ЛЧХ при изменении знака
коэффициента демпфирования
Рисунок 11 –
График ПХ, АФХ и ЛЧХ при изменении знака
коэффициента демпфирования
4. Ответы на вопросы
Вопрос 1. Как располагаются на комплексной плоскости корни хп при
= опт?
Ответ: симметрично относительно оси Х на расстоянии коэффициента демпфирования
Вопрос 2. Чему равна высота пика лачх?
Ответ:
5. Заключение
В ходе выполнения второго задания были определены переходные и частотные характеристики звена при k=10, T=5, ξ=0.4.
Проанализировано движение корней (траекторий корней) ПФ на комплексной плоскости при изменении параметра .
Определена зависимость резонансного пика АЧХ от коэффициента демпфирования и проведено ее сравнение с графиком теоретической зависимости.
Определена
зависимость резонансной частоты
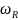 от постоянной времени T
и проведено ее сравнение с графиком
теоретической зависимости. Экспериментально
определено оптимальное значение
коэффициента демпфирования
из условия минимума времени
от постоянной времени T
и проведено ее сравнение с графиком
теоретической зависимости. Экспериментально
определено оптимальное значение
коэффициента демпфирования
из условия минимума времени
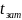 затухания процесса. Также была определена
высота пика ЛАЧХ при
:
затухания процесса. Также была определена
высота пика ЛАЧХ при
:
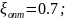

Определены переходные и частотные характеристики (АФХ и ЛЧХ) при изменении знака коэффициента демпфирования на .
Заключение
В ходе выполнения первого задания были составлены ММ в ПФ и ДУ:
ММ в ДУ:

ММ в ПФ:
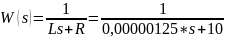 Для
каждой из моделей были получены переходные
характеристики. В результате сравнительного
анализа графиков сделан вывод об
эквивалентности моделей. С
помощью программных средств MATLAB
(Command
Window)
была построена ПФ объекта и получены
ПХ, ЛЧХ, АФХ и карта расположения корней
характеристического полинома.
Для
каждой из моделей были получены переходные
характеристики. В результате сравнительного
анализа графиков сделан вывод об
эквивалентности моделей. С
помощью программных средств MATLAB
(Command
Window)
была построена ПФ объекта и получены
ПХ, ЛЧХ, АФХ и карта расположения корней
характеристического полинома.
В ходе выполнения второго задания были определены переходные и частотные характеристики. Произведен анализ движения корней ПФ на комплексной плоскости при изменении параметра . Определены зависимость резонансного пика АЧХ от коэффициента демпфирования , а также зависимость резонансной частоты от постоянной времени T и проведено сравнение с графиком теоретической зависимости. Экспериментально определено оптимальное значение коэффициента демпфирования . Также была определена высота пика ЛАЧХ при :
Переходные и частотные характеристики звена определяются при изменении коэффициента демпфирования ξ на –ξ, что влечет за собой изменение направления графиков.