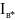15 Расчет и построение характеристик генератора

15.1. Статическая перегружаемость:

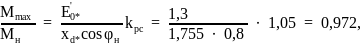
где k_рс = 1,05 для:

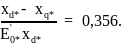
15.2. Угловая характеристика:

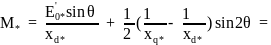
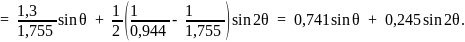
15.3. Регулировочная характеристика I_в* = f(I_*):

Для построения регулировочных характеристик достаточно задать три – пять значений тока якоря I_*, например, 0; 0,5; 1. По заданным значениям I_* для U_* = const и cos φ = const строят векторные диаграммы, из которых находят значения I_в*.

15.4. Внешняя характеристика U_* = f(I_*):

Внешнюю характеристику можно построить, используя семейство регулировочных характеристик [4]. Из точки, соответствующей U_* = 1 и I_* = 1, проведем прямую параллельно оси абсцисс. Точки пересечения этой прямой с регулировочными характеристиками дадут значения тока I_* при U_* = 1,1 и U_* = 1,15. Значение U_* при I_* = 0 получим по характеристике холостого хода для I_вн*. Данные расчета сведены в таблице 15.1.

Т а б л и ц а 15.1 – Расчетные значения для внешней характеристики

I*	0	0,5	1
U*	1,38	1,22	1

15.5. U-образная характеристика I_* = f( ):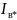

При построении U-образной характеристики должно быть обеспечено выполнение условий 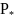= const и 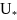= const. Принимая во внимание, что 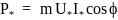, можно отметить, что активная составляющая тока якоря 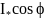также постоянна.

Для U-образной характеристики при U_* = U_н*, Р_* = Р_*н и cos φ = 0,8 активная составляющая тока равна 0,8. Для характеристик при 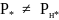, например при 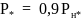, активная составляющая = 0,9 · 0,8 = 0,72 и т.д.

U-образную характеристику для случая Р_* = 0,8; U_* = U_н* строим следующим образом. Откладываем по оси абсцисс в масштабе вектор напряжения 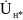. С ним совпадает по направлению вектор активного тока I_н*cos φ_н. Затем задаемся несколькими значениями тока I_*, например двумя I_(1)* = 1, I_(2)* = 0,9 для индуктивной нагрузки (φ > 0), одним для активной нагрузки I_(3)* = I_н*cos φ_н и одним I_(4)* = 0,88 для емкостной нагрузки (φ < 0). Определяем для этих токов углы φ. Данные расчёта сводим в таблицу 15.2.

Т а б л и ц а 15.2 - Расчетные значения для U-образной характеристики

	1,1	1,11	1,12
I*	0,93	0,9	0,95

U-образная характеристика I_* = f( ) может быть построена без учёта насыщения магнитопровода [5,6]. При этом будем считать синхронную машину неявнополюсной (аналогично допущению при построении диаграммы Потье) с синхронным индуктивным сопротивлением 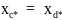. Учтём ранее указанное соотношение , откуда следует постоянство активной составляющей тока якоря . С другой стороны, электромагнитная мощность неявнополюсной машины 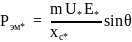. Пренебрегая незначительной разницей между его выходной электрической и электромагнитной мощностями, будем считать, что выполнение условия постоянства мощности, необходимого для построения U-образной характеристики, обеспечивается также постоянством произведения 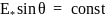(т.к. остальные параметры формулы для определения 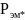являются постоянными). 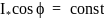Следствием полученных условий построения U-образной характеристики, а именно: и , является то, что конец вектора тока якоря при изменении угла φ перемещается вдоль линии тока I, а конец вектора ЭДС возбуждения – вдоль линии ЭДС E. Промежуточные относительные значения тока якоря и возбуждения могут быть получены пропорциональным пересчётом соответствующих длин векторов тока якоря и ЭДС возбуждения по отношению к указанным величинам для базовой векторной диаграммы для номинального режима. С учётом допущения о неучёте насыщения можно считать .