
тоэ3
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ТОЭ
отчет
по лабораторной работе №3
по дисциплине «Теоретические основы электротехники»
Тема: Исследование свободных процессов в электрических цепях
Студентка гр. 9493 |
|
Старикова А.С. |
Преподаватель |
|
Панкин В.В. |
Санкт-Петербург
2021
Цель работы.
Изучение связи
между видом свободного процесса в
электрической цепи и расположением
собственных частот (корней характеристического
уравнения) на комплексной плоскости;
приближенная оценка собственных частот
и добротности
 -
контура по осциллограммам.
-
контура по осциллограммам.
Основные теоретические положения.
В работе предлагается исследовать
свободные процессы в цепях, схемы которых
представлены на рис. 3.1 и рис. 3.2. Цепи
возбуждаются очень короткими импульсами
тока
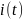 ,
заряжающими емкость
,
заряжающими емкость
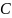 .
В паузах между импульсами емкость
разряжается, цепь находится в свободном
режиме, так как в это время источник
возбуждения отключен (
.
В паузах между импульсами емкость
разряжается, цепь находится в свободном
режиме, так как в это время источник
возбуждения отключен (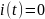 ).
).
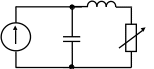
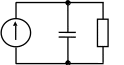
а б
Рис. 3.1
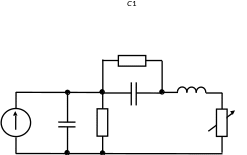
Рис. 3.2
В линейных цепях
свободный процесс описывается однородными
линейными дифференциальными уравнениями
и его вид определяется корнями
характеристического уравнения
(собственными частотами цепи
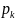 ).
При возбуждении цепи источником тока
собственные частоты можно рассчитать
как нули входной проводимости цепи
).
При возбуждении цепи источником тока
собственные частоты можно рассчитать
как нули входной проводимости цепи
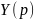 :
:
а) для цепи первого порядка, представленной
на рис. 3.1,а
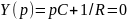 ,
откуда
,
откуда
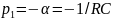 ;
(3.1)
;
(3.1)
б) для цепи второго порядка, представленной
на рис. 3.1, б
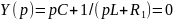 ,
откуда
,
откуда
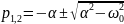 ,
,
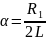 ,
,
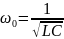 ;
(3.2)
;
(3.2)
в) для цепи третьего порядка, представленной
на рис. 3.2
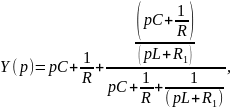 откуда
откуда
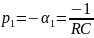 ,
,
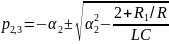 ,
,
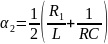 .(3.3)
.(3.3)
Общий вид решения для напряжения любого элемента цепи
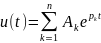 ,
,
где
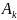 – постоянные интегрирования,
– постоянные интегрирования,
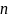 – порядок цепи.У цепи первого порядка
одна собственная частота (3.1), вещественная
и отрицательная, свободный экспоненциальный
процесс имеет вид
– порядок цепи.У цепи первого порядка
одна собственная частота (3.1), вещественная
и отрицательная, свободный экспоненциальный
процесс имеет вид
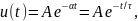 (3.4)
(3.4)
где
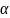 – постоянная затухания,
– постоянная затухания,
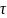 – постоянная времени экспоненты.
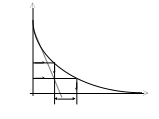
Временная диаграмма свободного процесса
показана на рис. 3.3, а, причем
– интервал времени, соответствующий
любой подкасательной к экспоненте.
– постоянная времени экспоненты.
Временная диаграмма свободного процесса
показана на рис. 3.3, а, причем
– интервал времени, соответствующий
любой подкасательной к экспоненте.
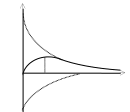
В цепи второго порядка две собственные
частоты (3.2) могут быть разными вещественными
различными (апериодический режим;
временная диаграмма суммы двух экспонент,
изображенных пунктиром, показана на
рис. 3.3, б), кратными вещественными
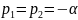 (критический режим) или комплексно-сопряженными
(колебательный режим). Вид критического
процесса
(критический режим) или комплексно-сопряженными
(колебательный режим). Вид критического
процесса
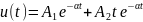 близок к диаграмме, показанной на рис.
3.3, б, причем момент достижения
максимума
близок к диаграмме, показанной на рис.
3.3, б, причем момент достижения
максимума
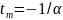 ,
если
,
если
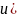 .
Комплексно-сопряженным частотам
соответствует качественно новый характер
свободного процесса – колебательный:
.
Комплексно-сопряженным частотам
соответствует качественно новый характер
свободного процесса – колебательный:
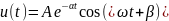 ,
(3.5)
,
(3.5)
где
– постоянная затухания,
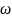 – частота затухающих колебаний (
– частота затухающих колебаний (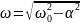 ).
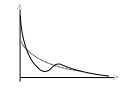
Временная диаграмма колебательного
процесса представлена на рис. 3.3, в.
).
Временная диаграмма колебательного
процесса представлена на рис. 3.3, в.
Дальнейшее увеличение порядка цепи к
качественно новым явлениям не приводит.
Так, согласно (3.3), в схеме, изображенной
на рис.3.2, собственные частоты могут
быть либо три вещественные, либо одна
вещественная и две комплексно-сопряженные,
например,
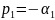 и
и
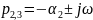 .
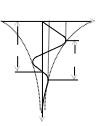
Временная диаграмма свободного процесса
представлена на рис. 3.3, г – это сумма
экспоненты (см. пунктир) и затухающей
синусоиды.В некоторых случаях собственные
частоты относительно просто рассчитываются
по осциллограммам. Например, согласно
(3.4) по рис. 3.3, а можно рассчитать
постоянную затухания
.
Временная диаграмма свободного процесса
представлена на рис. 3.3, г – это сумма
экспоненты (см. пунктир) и затухающей
синусоиды.В некоторых случаях собственные
частоты относительно просто рассчитываются
по осциллограммам. Например, согласно
(3.4) по рис. 3.3, а можно рассчитать
постоянную затухания
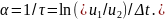 (3.6)
(3.6)
Для случая рис. 3.3, в постоянная
затухания также может быть определена
на основании (3.6), но при этом обязательно
выполнение условия
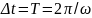 ,
что вытекает из (3.5).
,
что вытекает из (3.5).
а б
в г

Рис. 3.3
В случаях рис. 3.3, б,г найти собственные частоты можно лишь приближенно, выделив, как показано пунктиром, отдельные составляющие процесса.
Особый интерес для
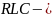 контуров
представляет определение добротности
контуров
представляет определение добротности
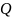 по виду свободного процесса в них. Так
для последовательного
контура
добротность определяется выражением
по виду свободного процесса в них. Так
для последовательного
контура
добротность определяется выражением
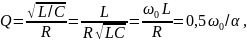 (3.7)
(3.7)
где
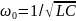 – частота незатухающих колебаний в
идеальном контуре (
– частота незатухающих колебаний в
идеальном контуре (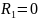 ).
Согласно (3.2) собственные частоты
последовательного
контура
можно записать следующим образом:
).
Согласно (3.2) собственные частоты
последовательного
контура
можно записать следующим образом:
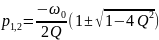 ,
(3.8)
,
(3.8)
причем
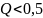 соответствует апериодический режим,
соответствует апериодический режим,
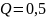 – критический режим,
– критический режим,
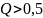 –
колебательный режим, а
–
колебательный режим, а
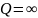 –незатухающий колебательный режим.
–незатухающий колебательный режим.
При
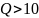 с высокой степенью точности можно
считать
с высокой степенью точности можно
считать
 (3.9)
(3.9)
С учетом (3.6) формула, позволяющая в этом случае определить добротность по осциллограмме рис. 3.3, в, имеет вид
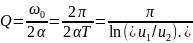 (3.10)
(3.10)
Для повышения точности можно брать отношения напряжений за периодов колебаний:
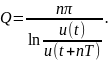 (3.11 )
(3.11 )
Обработка результатов эксперимента.
Исследование свободного процесса в цепи первого порядка
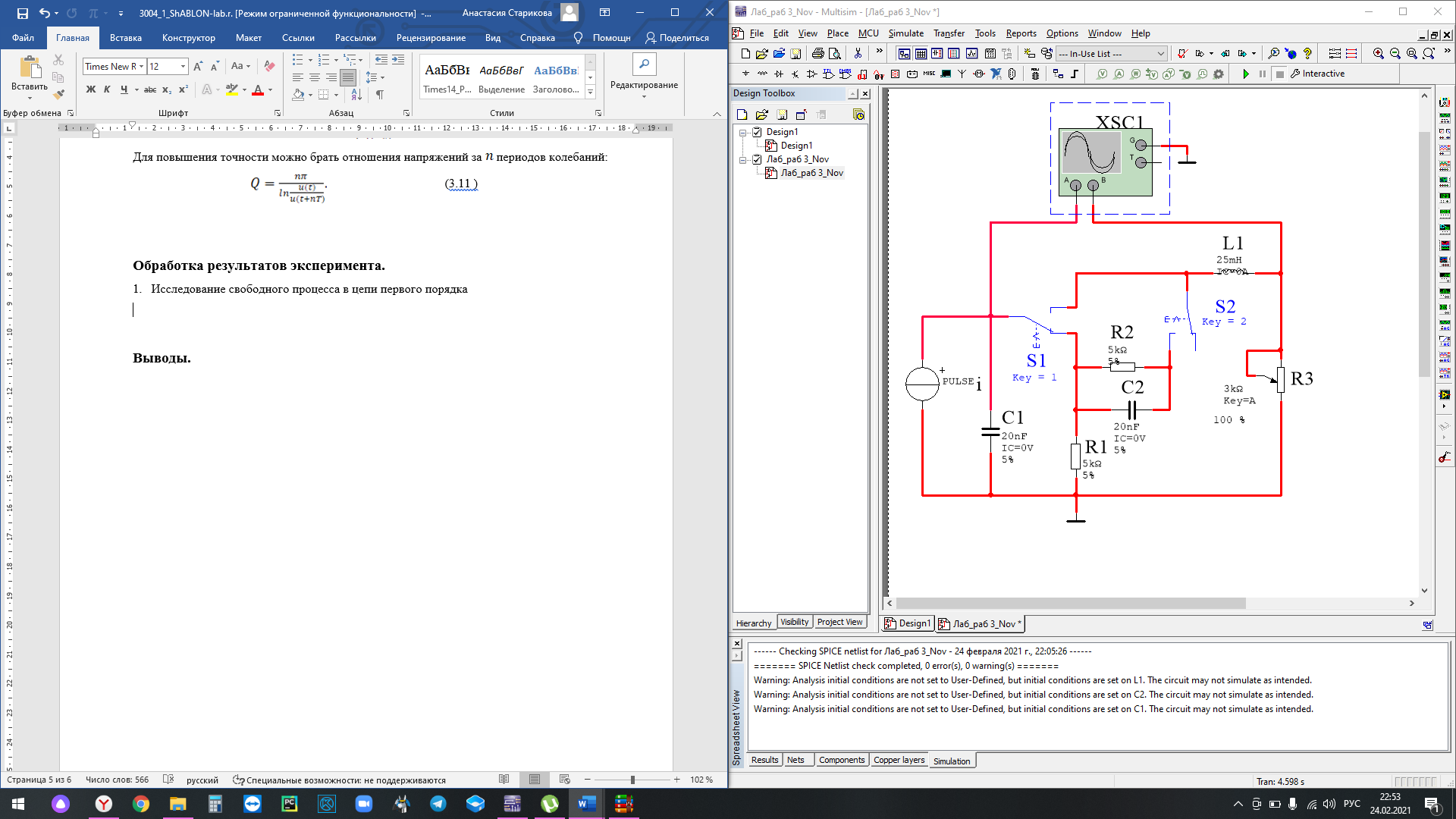
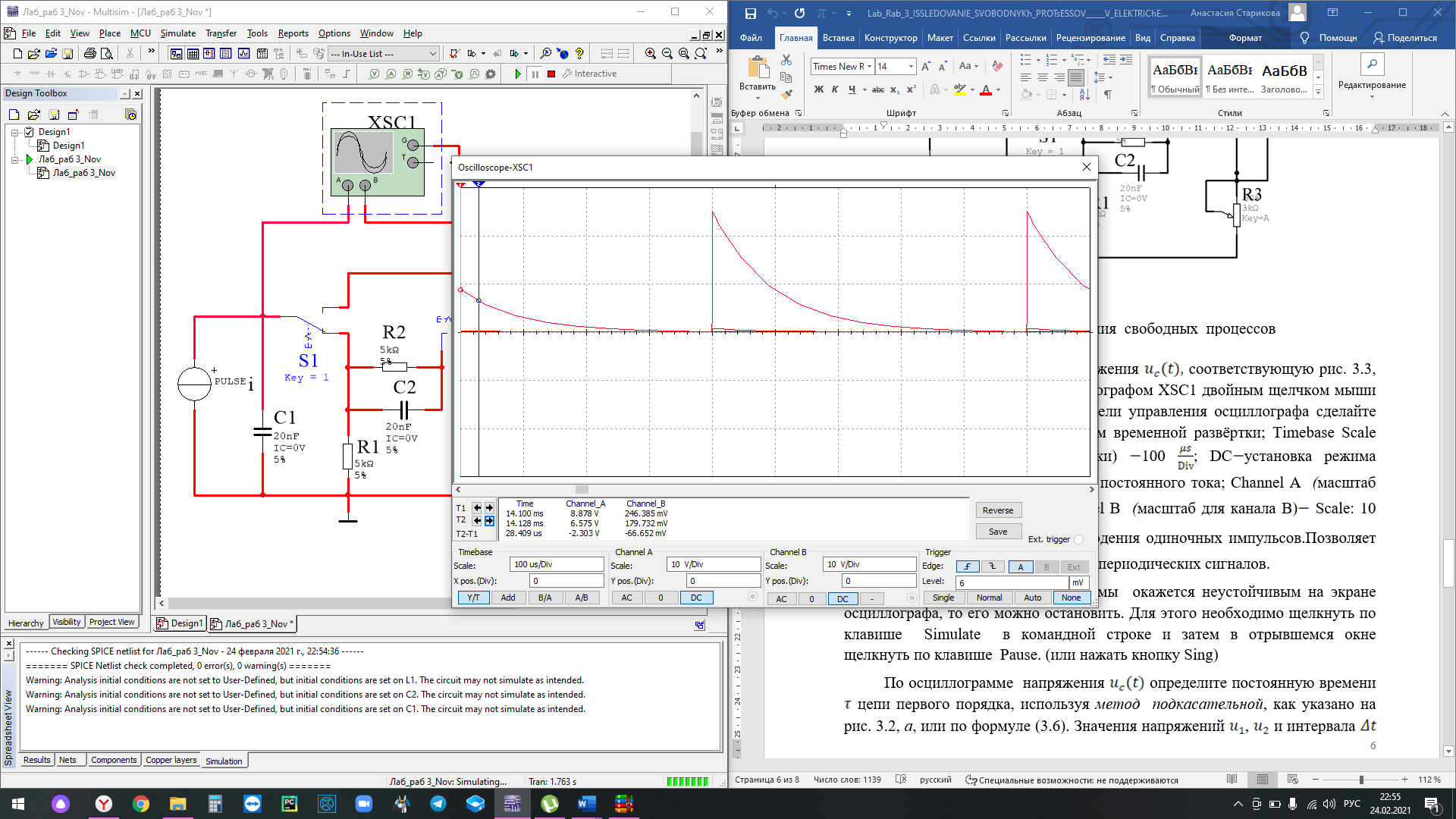
Расчет собственной частоты:
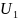 = 8.878 V
= 8.878 V
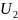 = 6.575 V
= 6.575 V
∆T
= 28.409*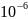 (с)
(с)
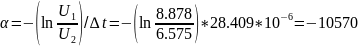
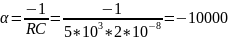
Можно сделать вывод о том, что найденная частота соответствует практической с минимальной погрешностью.
Исследование свободных процессов в цепи второго порядка
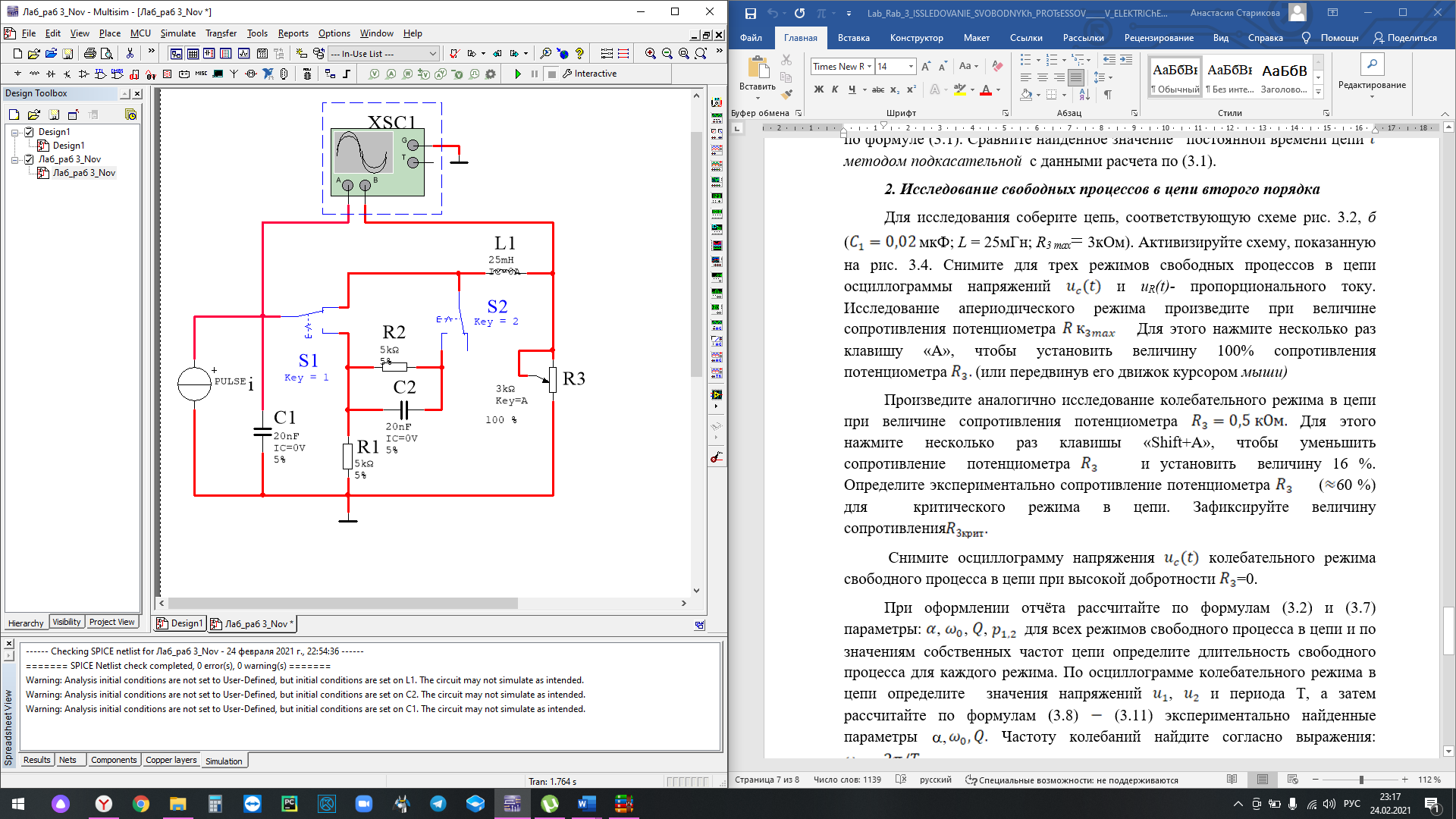
Апериодический режим:
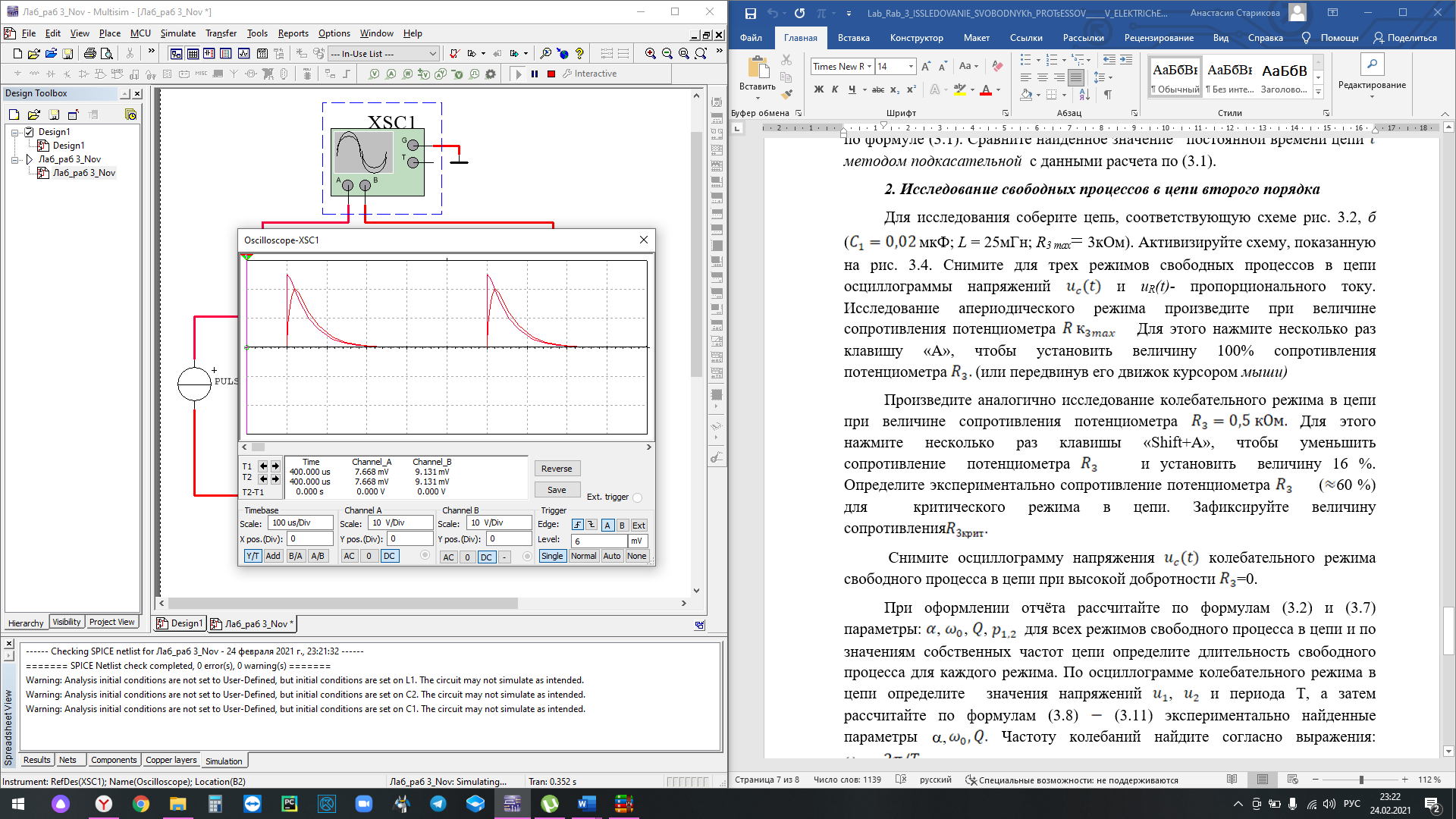
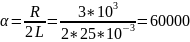
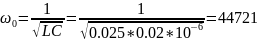
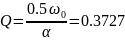
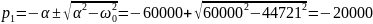
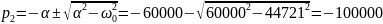
Длительность свободного процесса апериодического режима:
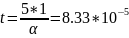
Колебательный режим:
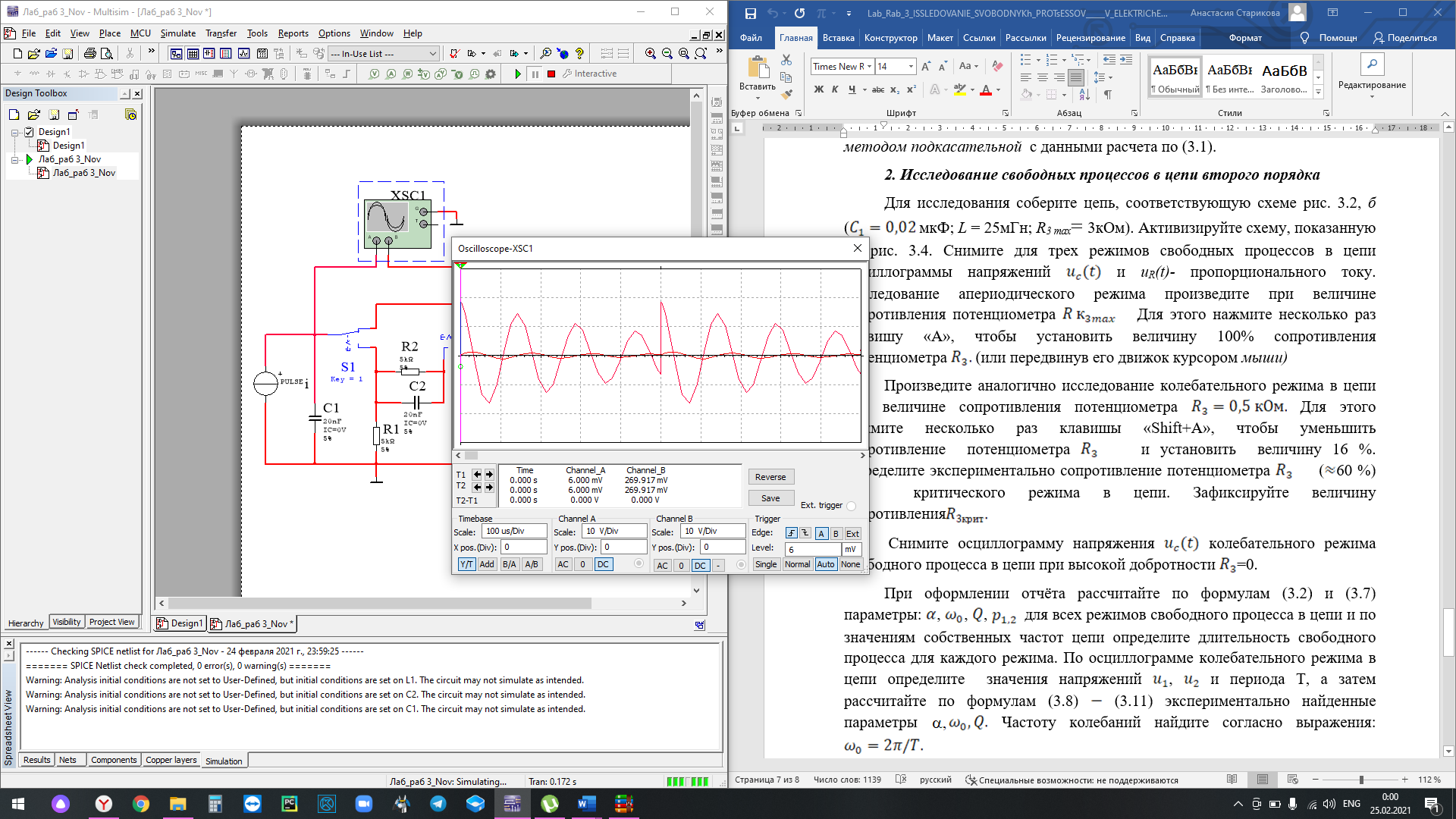
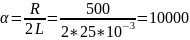
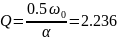
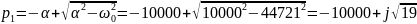
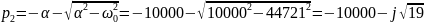
Длительность свободного процесса апериодического режима:
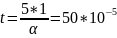
= V
= V
