ПЗ 5

ление

наложены ограничения типа

неравенства. Постановка задачи

с ограничением на управления в общем случае имеет вид:

1)

Уравнения движения объекта управления

= ( 1

2

̇= ( , , ),

= 1, 2, … , ,

где

… )

= ( 1

2

… ) – вектор управляющих переменных.

2)

Ограничения на управление

,

– допустимое множество значений управления.

где Часто ограничение на управления имеет вид неравенства:

3)

Граничные условия

≤ .

= ,

= 1, 2, … , .

( 0) = 0;

или в более общем случае

, = 0,

= 1, 2, … , .

( 0), , 0

4)

Критерий оптимальности

= 0 ( 0), , 0, + 0( , , ) .

0

вместо условия стационарности записывается принцип максимума.

Алгоритм решения задачи с помощью принципа максимума Понтря-

гина включает следующие действия:

1)

Составить гамильтониан

= ,

где

0 = −1

=0

.

2)

Составить уравнения Эйлера–Лагранжа

̇

= 1, 2, … , .

= − ,

3)

Записать принцип максимума

= (

,

,

, ),

max (

, ,

, )

из которого выразить управляющие переменные

(

) и под-

ставить в уравнения движения. Получится

система дифференциальных

= 1, 2, … ,

уравнений:

̇= ( , , ),

= 1, 2, … , .

мых

При анализе условия максимума может получиться, что управляющие

должны принимать значения на границе области допусти-

переменные

значений. При этом возможны скачкообразные изменения величины

| | ≤

−

.

Например, если область допустимых значений задана неравенством

, то

может менять значение с

на

. Такие моменты времени

будут называться точками переключения.

1

Точки переключения делят весь процесс от начальной точки

до ко-

нечной

на интервалы. Например, в случае одной точки переключения0

Задание

При наличии ограничения на управление

требуется перевести

= 0

заданное время

.

объект на максимальное перемещение 1

за

| | ≤

Начальное время 0

Уравнения движения, граничные условия

.

( )

( )

и конечное время

( ),

заданы в табл. 4 по вариантам.

.

Постройте графики

1

2

и график функции управления

Таблица 1 Исходные данные для расчета

1

Уравнения

,

1

1

̇1 = 2

− 2

Вариант

движения

Граничные условия

2

̇2 =

+ 2

1

( 0)

= 2

( 0)

= 0,

2

= 0

0,5

2

̇1 = 2

1

( 0)

= 2

( 0)

= 0

2

= 0

3

̇2 = − 1

+

1

( 0)

= 0, 2( 0) = 4

,

2

= 0

1,5

1

̇1 = 2

− 1

4

̇2 = −1

+

1

( 0)

= 2( 0)

= 2

,

2

= −2

2

2

̇1 = 2

+

5

̇2 = 1

+

1

( 0)

= −2, 2( 0) = 2

,

2

= −10

2,5

2

̇1 = −2

+

6

̇2 = 1

+

,

3

1

̇1 = 2

− 4

1

( 0)

2

( 0)

( 2)

7

̇2 =

+ 5

=

= 0,

= 1

2,2

2

̇1 = 2

1

( 0)

= 2

( 0)

= 0

2

= 0

8

̇2 = − 1

+ 2

1

( 0)

= 0, 2( 0) = 2

,

2

= 0

0,8

1

̇1 = 2

− 3

9

̇2 = 1

+

1

( 0)

= 2( 0)

= 2

,

2

= −2

2,8

1

̇1 = 2

+

10

̇2 = −1

+

1

( 0)

= −1, 2( 0) = 1

,

2

= −4

3,2

2

̇1 = −2

+

11

̇2 = 1

+ 2

1

( 0)

= 2( 0)

= 10

,

2 = 0

1,2

1

̇1 = 2

+ 5

12

̇2 = −1

+

,

1,6

2

̇1 = −2

+

1

( 0) = −1, 2( 0) = 1

2

= 0

̇2 = 1

+ 3

Исходные данные:

̇1 = 2;

:2, = 1)..

Ограничение( =

1)

Уравнения движения:

2)̇2 =

(0) = 0

= 0

= 10 с

4)

(0) =

3)

Граничные

условия:

| | ≤ 5

1

2

,

2

,

.

1

равен:

Критерий оптимальности в случае максимального перемещения

Решение= −1 : → .

1)

Гамильтониан:

= 1 1

+ 2

2 = 1 2

+ 2 .

=

=0

3)

=

= −

+

Решение данной системы уравнений с точностью до постоянных ин-

тегрирования:

1

1

,

2

1

2

.

Условие принципа максимума:

+ max(

).

max|

= max(

+

2

) =

2

|≤5

| |≤5

1

2

1

2

| |≤5

принимает

значение

5 или

–5 в

зависимости =от5sign(

2

)

Из условия принципа максимума следует, что

. То есть

знак= − +

знака

функции

2

1

2

. Так как функция

2

линейная, то она может изменить

только один раз и может быть только одна точка переключения. Обо-

5, при0 ≤ ≤ 1,

или

−5, при 0 ≤ ≤ 1

,

значим момент ереключения 1

. Возможно два варианта:

( ) =

1

( ) =

1

Далее

−5, при

< ≤

5, при

< ≤ .

необходимо полностью выполнить решение для обеих гипотез

и выбрать ту из них, для которой ответ получится оптимальным.

( ) =

5, при 01≤ ≤ 1,

Для начала рассмотрим первую гипотезу:

−5, при

< ≤ .

(0) = (0) = 0

условий в начальный момент времени

1

С

учетом

граничных

2

решение данной системы дифференциальных уравне-

ний будет следующим:

11

= 5 2,

21 = 5 .

2

1 < ≤

,

= −5

̇1 = 2;

б)

Второй участок

.

̇2 = −5.

С учетом граничного условия в конечный момент времени

2

иметь одну

решение данной системы дифференциальных уравнений будет

(10) = 0

Для

= + (50 −

5 ),

= 50 −5 .

произвольную постоянную:

22

12

1

определения постоянной

и времени переключения

запишем

11( 1) = 12( 1),

условия неразрывности:

21( 1) = 22( 1);

25

112

= + 1

(150 −5 1),

5

= 50 −5 .

1 = 5

= −125

Решив данную систему уравнений, получим:

c,

.

5) Таким образом, оптимальные управляющая переменная и пере-

5, при 0 ≤ ≤ 5 с,

менные состояния будут равны:

( )

= −5, при 5 < ≤ 10 с;

1

5

2, при 0 ≤

≤ 5 с,

2

2

( ) = 5

+ (50 −

5 ), при 5 < ≤ 10 с;

2

2

5 , при 0 ≤ ≤ 5 с,

( ) = 50 −

5 , при 5 < ≤ 10 с.

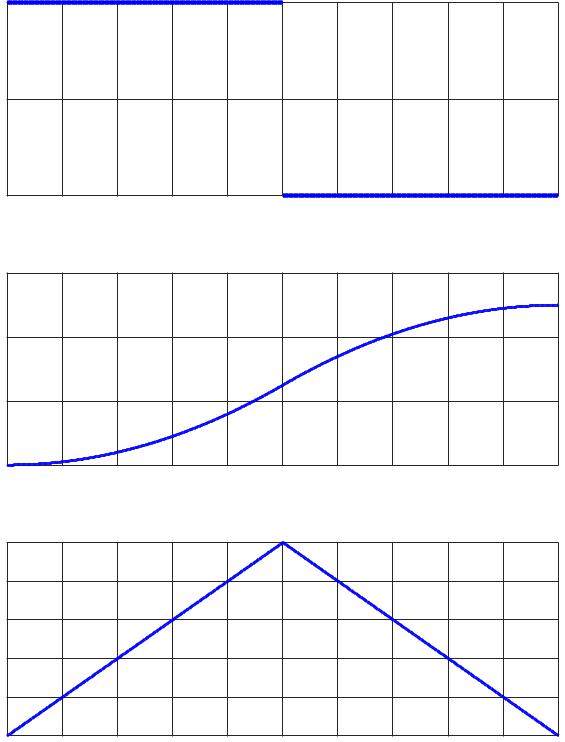
1( ), 2

( )

( )

и переменных состояния

Графики функции управления

представлены на рис. 1.