5 семестр (вечерка) / Лаболаторные работы / Лабараторная работа №3, вторая. Исследование свободных процессов в электрических цепях / Лабараторная работа №3, вторая. Исследование свободных процессов в электрических

Федеральное государственное автономное образовательное учреждение высшего образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)»

Кафедра теоретических основ электротехники

ОТЧЕТ

по лабораторной работе № 3

«Исследование свободных процессов в электрических цепях»

Выполнил : Попов Алексей Павлович

Группа № 9802

Преподаватель: Езеров Кирилл Сергеевич

Оценка лабораторного занятия
Вопросы	Подготовка к лабораторной работе	Отчет по лабораторной работе	Коллоквиум	Комплексная оценка

Санкт-Петербург, 2021

ЛАБОРАТОРНАЯ РАБОТА № 3

Исследование свободных процессов в электрических цепях

Работа № 3. Исследование свободных процессов в электрических цепях

Цель работы: изучение связи между видом свободного процесса в электрической цепи и расположением ее собственных частот (корней характеристического уравнения) на комплексной плоскости; экспериментальное определение собственных частот и добротности RLC-контура по осциллограммам.

Схема установки

Схема установки исследования свободных процессов в электрических цепях представлена на рисунке 1.

Р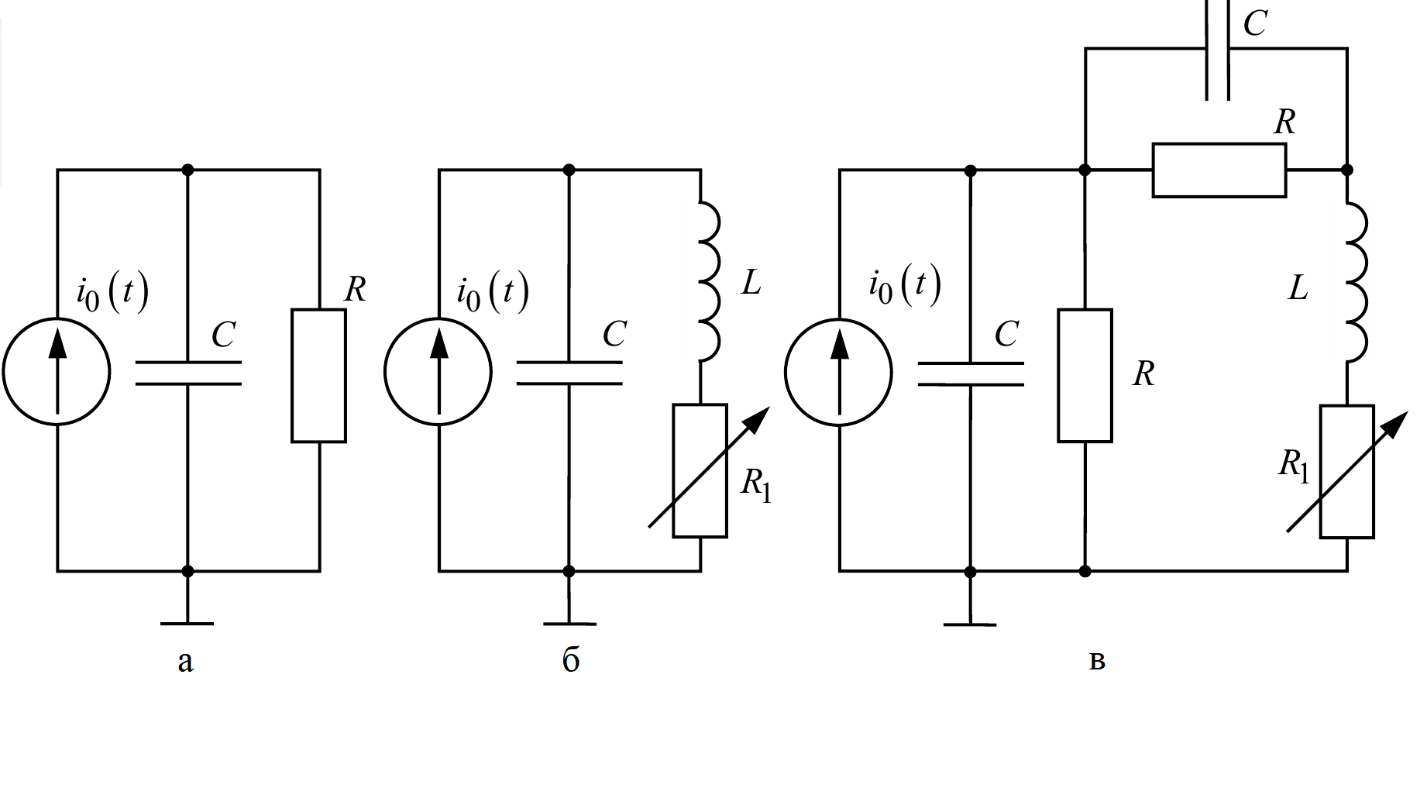 ис. 1. Схема установки исследования свободных процессов в электрических цепях: а – первого порядка, б – второго порядка, в – третьего порядка.

Основные расчетные формулы.

1. Формула для расчета собственной частоты p₁ (Гц) у цепи первого порядка: p₁ = 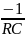, где R – сопротивление резистора (Ом), C – емкость конденсатора (Ф).

Собственная частота p₁ по осциллограмме:

p₁= -α = 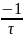, где α – постоянная затухания, для осциллограммы: α=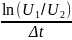 , 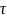– постоянная времени. И U₁ – напряжение по осциллограмме в момент времени t₁, U₂ - напряжение по осциллограмме в момент времени t₂. Δt = t₂-t₁

2. Формула для расчета собственной частоты p_1,2 (Гц) у цепи второго порядка при колебательном процессе: p_1,2 = -α ± 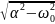*j, где

α = R₁/(2L), 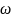₀ = 1/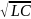 . L – индуктивность катушки (Гн).

Частота ω = 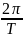, где T – период.

Собственная частота p_1,2 по осциллограмме должная удовлетворять условию Δt=T!

3. Формула для расчета собственной частоты p_1,2 = p₁ = p₂ по осциллограмме для критического режима:

p_1,2=-α = 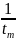, где

t_m – момент наступления максимума.

4. Формула для расчета экспериментальной добротности цепи второго порядка Q:

Q =

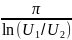
5. Формула для расчета теоретической добротности Q цепи второго порядка: Q=

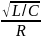
ПРОТОКОЛ НАБЛЮДЕНИЙ

Лабораторная работа №3

Исследование свободных процессов в электрических цепях

Осциллограммы зафиксированы на фотографиях.

Экспериментальный макет:

Для схемы а: C = 0,02 мкФ, R = 5 кОм.

Для схемы б: C = 0,02 мкФ, L = 25 мГн. Сопротивление критического режима R­­­_к = 1,3 кОм.

Выполнил Попов А.П.

Факультет электроники

Группа № 9802

“____” __________ _____

Преподаватель: ______________

Обработка результатов эксперимента

3.2.1. Исследование свободных процессов в цепи первого порядка

Теоретическая собственная частота цепи:

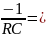
p₁ = 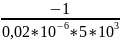= -10 000 с^-1 = -10⁴ с^-1

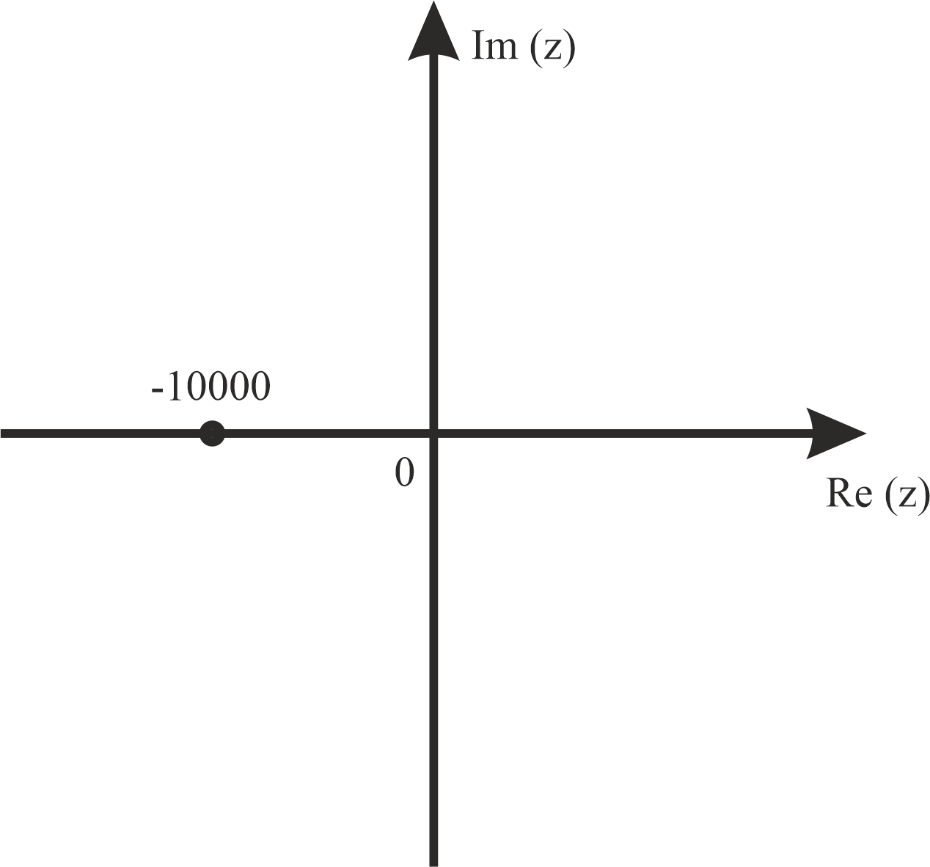
Рис.1 Диаграмма расположения собственной частоты цепи первого порядка.

Собственная частота цепи по осциллограмме:

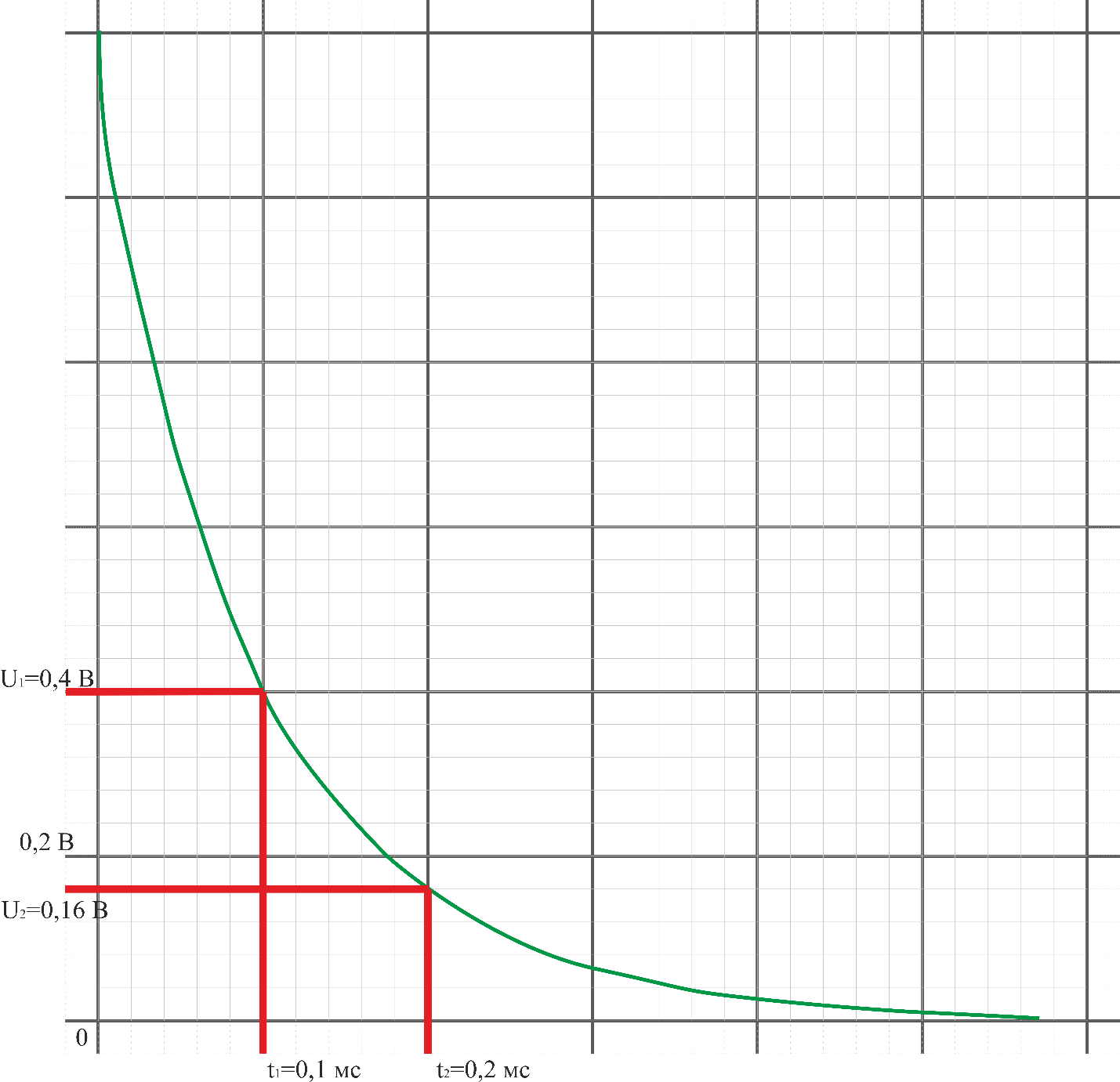
График 1. Осциллограмма свободного процесса в цепи первого порядка

p₁= -α = ; α = = 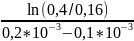≈-9162,90731с^-1.

p₁≈-9,1629 *10³ с^-1.

3.2.2. Исследование свободных процессов в цепи второго порядка

Теоретическая собственная частота цепи при R₁ = 0,5 кОм (колебательный процесс):

p_1,2 = -α ± *j;

α = R₁/(2L) = 0,5*10³/(2*25*10^-3)=10000.

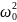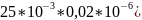= 1/LC=1/( =2 000 000 000.

p_1,2 ≈ -(10⁴)±4,36*10⁴*j с^-1;

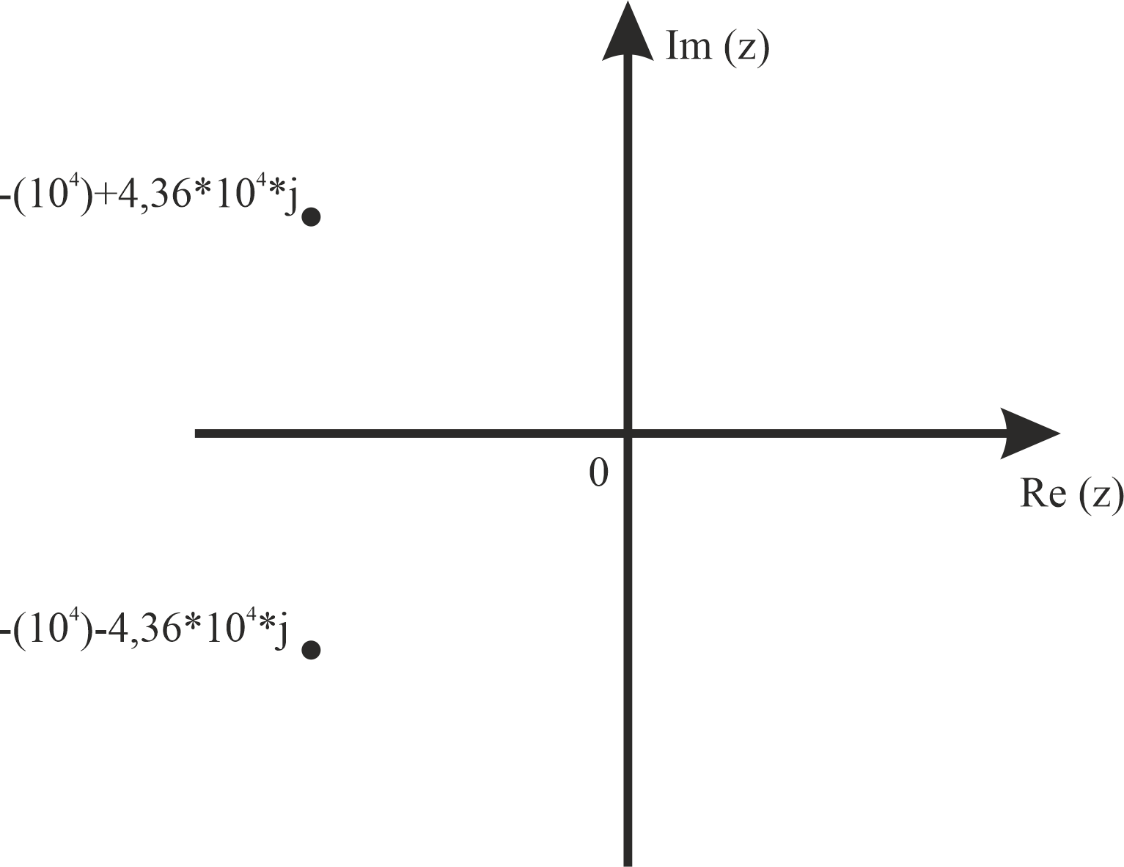
Рис. 2. Диаграмма расположения собственной частоты в цепи второго порядка. Колебательный режим

Собственная частота цепи по осциллограмме (T=0,00011с):

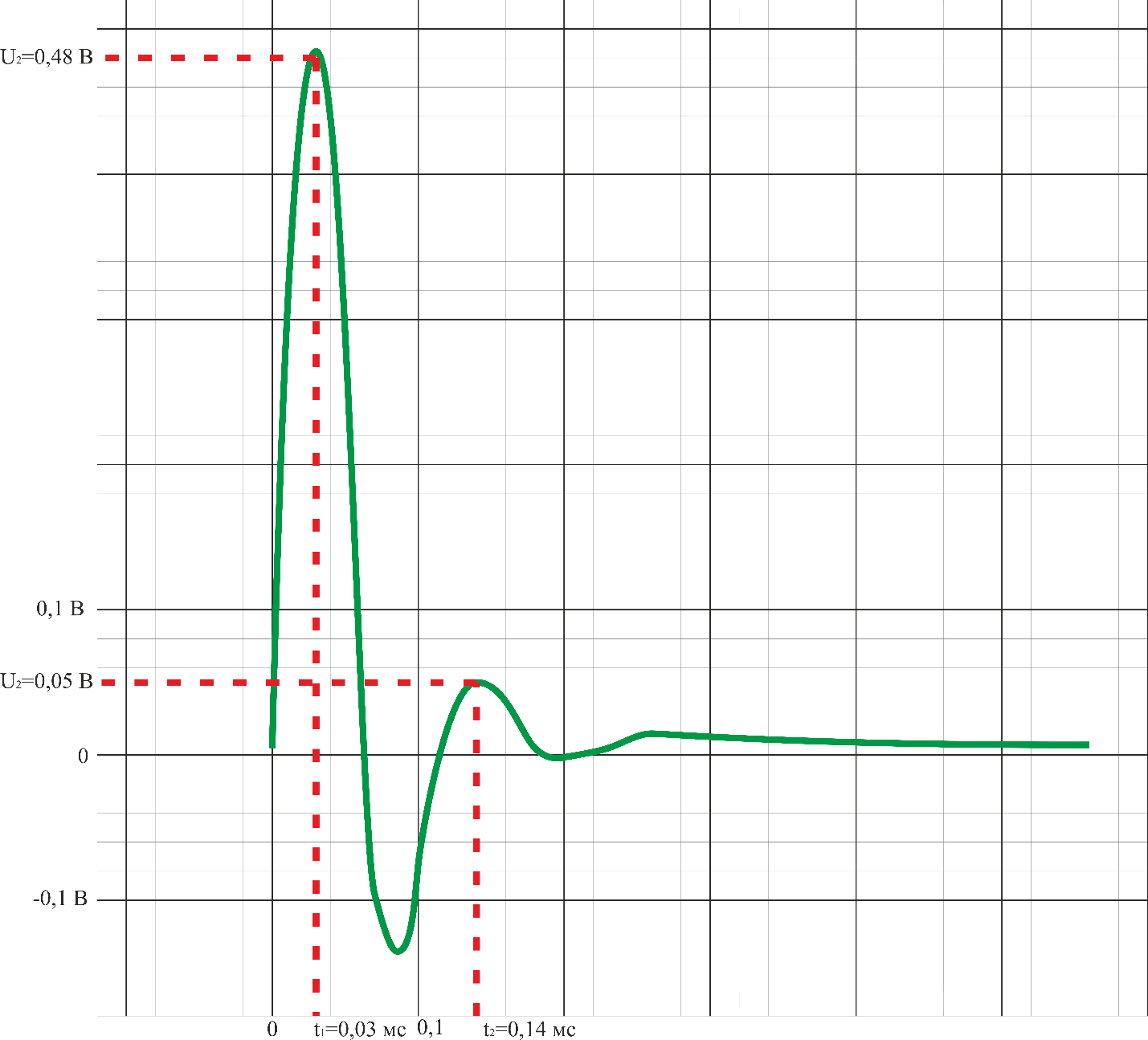
График 2. Осциллограмма колебательного процесса в цепи второго порядка

p_1,2=-α ± jω= ; α = = 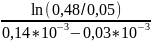≈20561,4827 с^-1.

ω = ≈ 57119,8664 с^-1.

p_1,2 ≈ -2,06*10⁴ ± 5,71*10⁴*j с^-1.

Теоретическая собственная частота цепи при R₁ = 3 кОм (апериодический режим, вопрос 5):

p_1,2 = -α ± ;

α = R₁/(2L) = 3*10³/(2*25*10^-3)=60000.

= 1/LC=1/( =2 000 000 000

p_1,2 ≈ -(6*10⁴)±3,64*10⁴ с^-1.

Рис. 3. Диаграмма расположения собственной частоты в цепи второго порядка. Апериодический режим

Собственная частота цепи по осциллограмме:

p_1,2=-α ± jω= ; α = = 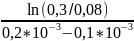≈ -13217,5584 с^-1.

ω = ≈ 1102,3132 с^-1.

p_1,2 ≈ -1,32*10⁴ ± 1,10*10⁴ с^-1.

Теоретические выкладки для апериодического режима выполняются в обоих случаях, но в связи износом исследуемой схемы, найденные теоретически и определенные экспериментально значения не совпадают.

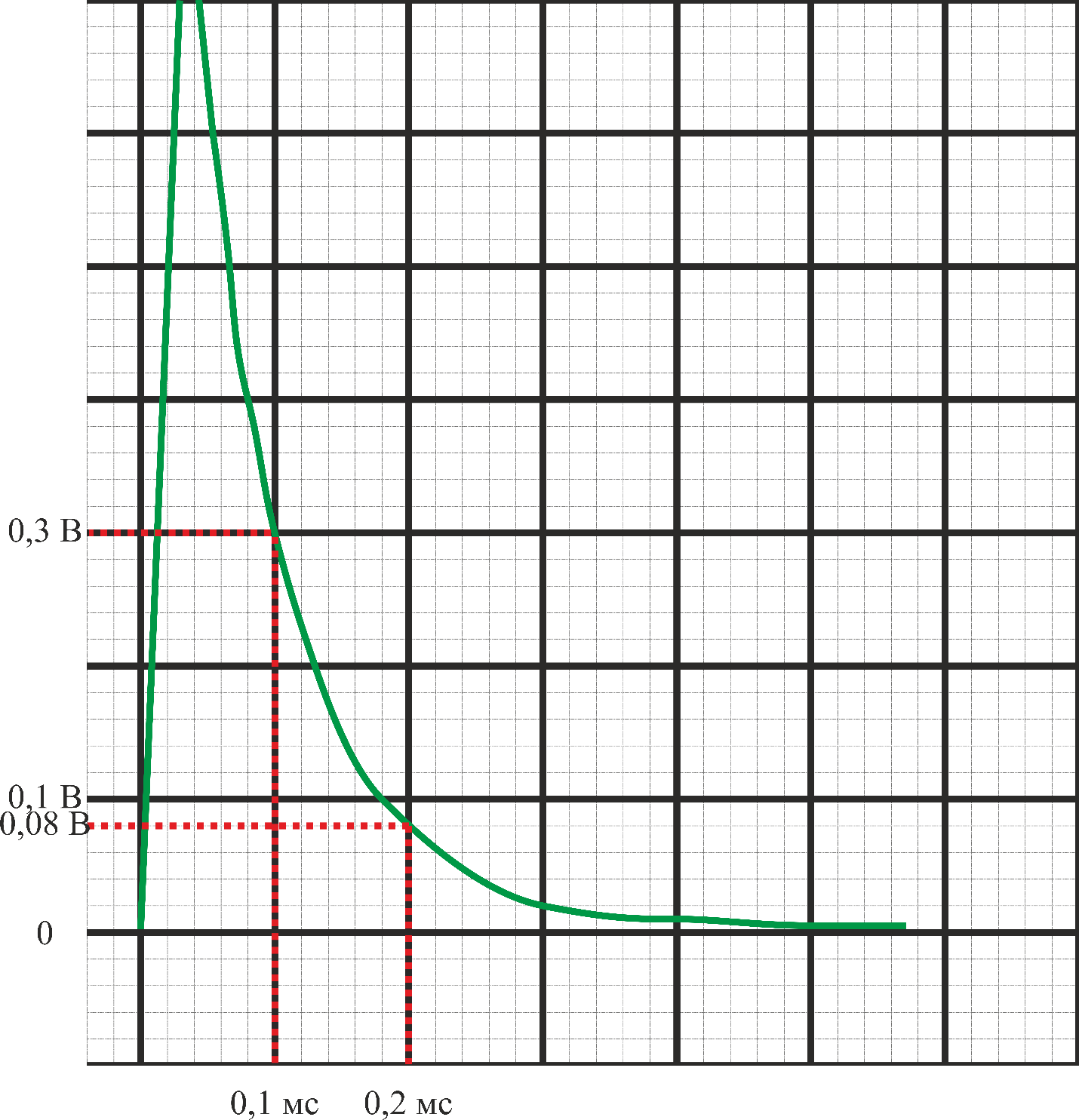
График 3. Осциллограмма апериодического режима

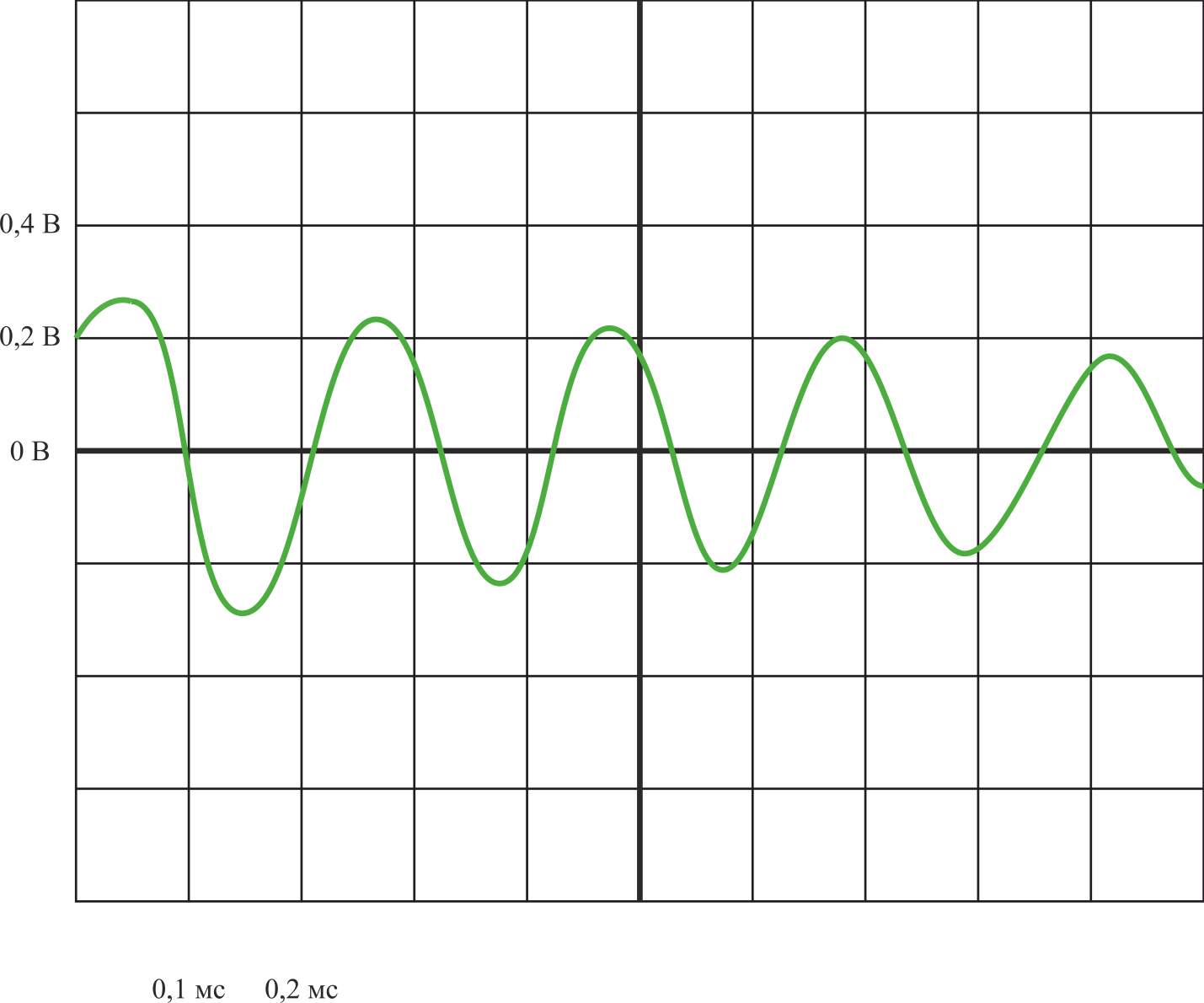
График 5. Осциллограмма конденсатора при R = 0

Теоретическая собственная частота цепи при R₁=R_кр=1,3 кОм (установленный по осциллограмме критический режим):

p_1,2 = -α ± ;

α = R₁/(2L) = 1,3*10³/(2*25*10^-3)=26000.

= 1/LC=1/( =2 000 000 000

p_1,2 ≈ -(2,6*10⁴)±3,64*10⁴ с^-1;

Для установки действительного критического режима правая часть выражения должна быть равна нулю, что возможно только при R₁≈2 236,0679 Ом. Найденный экспериментально критический режим отличается от теоретического на большую величину. На диаграмме будет представлено расположение собственной частоты при α = 2236,0679/(2*25*10^-3) ≈ 4,47*10⁴.

p_1,2 ≈ -4,47*10⁴

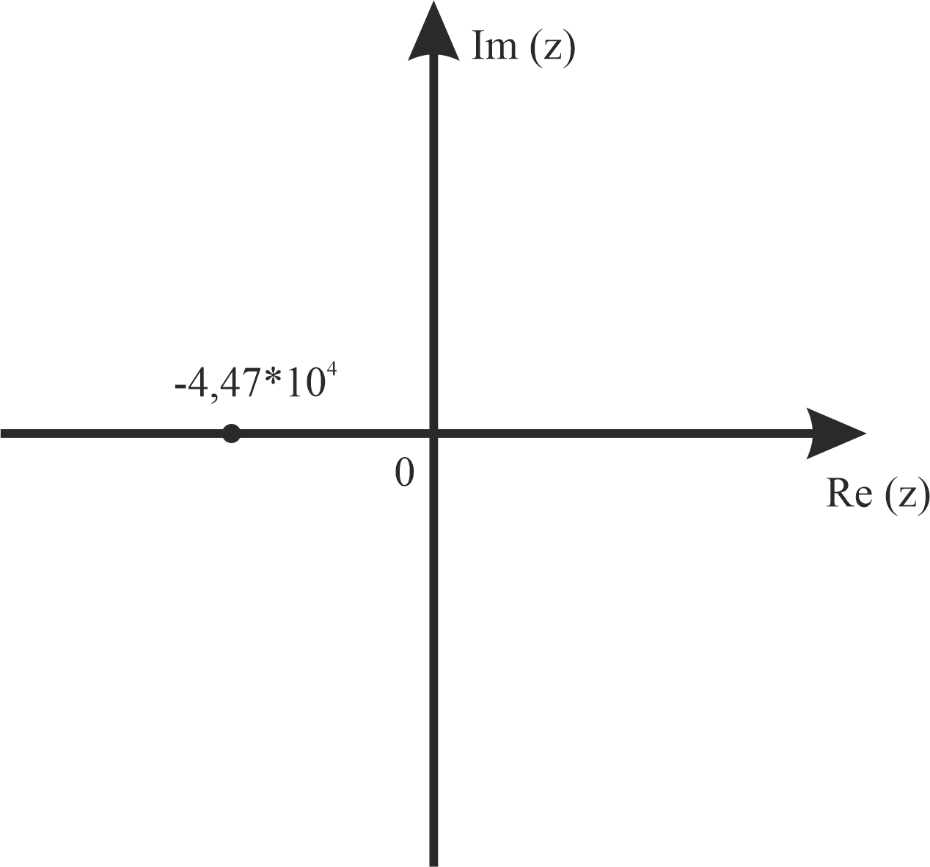
Рис. 3. Диаграмма расположения собственной частоты в цепи второго порядка. Критический режим

Собственная частота цепи по осциллограмме (t_m=0,022*10^-3с):

p_1,2=-α = = -45 454,54(54) ≈ -4,5*10⁴ с^-1.

График 6. Осциллограмма критического режима

Собственная частота цепи по осциллограмме различается от действительной теоретической на относительно малую величину, что говорит о неверных значениях сопротивления на переменном резисторе.

Добротность контура при R₁ = 0,5 кОм.

Q= =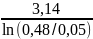 =1,3890…≈1,39

Добротность контура при R₁ = 0 Ом.

Q= =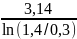 =0,6731…≈0,67

Расчет теоретического значения собственной частоты контура для цепи третьего порядка:

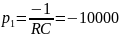
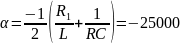
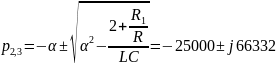
Рис. 4. Диаграмма расположения собственной частоты в цепи третьего порядка.

Контрольные вопросы.

1. U_c = Ae^-10000t.

2. С большой погрешностью, но соответствуют.

3. U(t) =

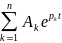
4. Найденные собственные частоты сильно отличаются от выполненного теоретического расчета. Что может быть вызвано износом RLC-компонентов или исследуемой схемы.

6. Теоретическая добротность контура при R₁ = 0.5 кОм:

Q= =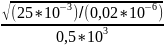 =0,2236… ≈ 2,24

Теоретические добротности процессов колебательного режима при R₁ = 0.5 кОм не совпадают с экспериментальными в связи с износом исследуемой схемы, но соответствуют протекающим процессам. Для колебательного процесса: Q>0.5.

Вывод

Проведено связи между видом свободного процесса в электрической цепи и расположением ее собственных частот (корней характеристического уравнения) на комплексной плоскости. Составлены диаграммы расположения собственных частот цепи на комплексной плоскости, обработаны осциллограммы свободных процессов в цепях. Большинство теоретических выкладок далеки от значений, найденных экспериментально. Так как в формулах расчета теоретических значений переменными являются значения индуктивности, емкости и сопротивления исследуемых элементов, можно судить что различия в значениях собственной частоты вызваны отличием действительного значения характеристик этих элементов от используемых при экспериментальных исследованиях. Так как практически все исследуемые процессы соответствуют теоретическим, но расходится только по значениям частот.