Указания по обработке результатов и содержанию отчета
1.По результатам измерений построить график зависимости тока диода от напряжения смещения (вольтамперную характеристику). Для каждой пары значений ток – напряжение указать на графике доверительные интервалы.
2.Из графика найти значения U1, U2 и I1. Оценить доверительную по-
грешность этих результатов.
3. По полученным в предыдущем пункте результатам оценить положение уровня Ферми, максимума плотности распределения электронов в зоне проводимости по отношению к дну зоны проводимости EC, а также вероятность туннелирования электронов через р–n-переход. Экспериментальные результаты сравнить с результатами предварительных расчетов.
4. Сформулировать выводы по работе.
Таблица 1
N = |
..., P = 95 %, u |
P,N |
= ... |
|
|
|
|
|
№ |
|
1 |
2 |
… |
N – 1 |
N |
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
x |
= |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
R |
x |
= x |
N |
−x |
= |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
U |
xi |
= x |
+1 |
– x |
|
|
|
|
– |
U |
x |
= u |
P,N |
R |
x |
= |
|
i |
i |
|
|
|
|
|
|
|
|
|
|
Если U xi U x , то результатов, содержащих грубые погрешности, в выборке нет.
Таблица 2
Обработка данных прямых измерений выборочным методом
|
|
|
N = ..., P = 95 %, t |
P,N |
= ..., |
P,N |
= ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
x |
− x |
2 |
|
x = t |
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = |
x |
|
|
|
|
|
|
|
|
R |
|
= x |
|
− x |
|
N |
i |
|
S |
x |
= |
N |
N −1 |
|
|
|
|
|
P,N |
|
x |
|
x |
|
max |
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продолжение табл. 2
Данные прямых и косвенных измерений.
Таблица 3
N = |
..., P = 95 %, u |
P,N |
= ... |
|
|
|
|
|
|
№ |
|
|
|
1 |
2 |
… |
N – 1 |
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
= |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yi |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
fi = f (xi , yi , ... ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fi = f (xi , yi , ... ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fi |
|
|
|
|
|
|
|
|
R |
f |
= f |
N |
|
− f |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
U |
fi |
= f |
i+1 |
− f |
i |
|
|
|
|
|
– |
U |
f |
= u |
P,N |
R |
f |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U f , то результатов, содержащих грубые погрешности, в выборке функции нет.
Таблица 4
Обработка данных косвенных измерений выборочным методом.
N = ..., P = 95 %, tP,N = ..., P,N = ... ,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fi |
|
|
|
fi − f |
f = t |
|
S |
|
|
R |
|
= f |
|
− f |
|
Формула |
|
f = |
|
|
|
|
|
P,N |
|
|
f |
max |
min |
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
N |
S f |
= |
N N −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значения коэффициентов Стьюдента |
tP |
рительной погрешности по выборке объема сти P = 95 % .
для расчета случайной дове-
при доверительной вероятно-
№ |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
100 |
t |
12.7 |
4.3 |
3.2 |
2.8 |
2.6 |
2.5 |
2.4 |
2.3 |
2.3 |
2.0 |
P,N |
для расчета случайной доверительной погрешно-
сти по размаху выборки
ятности Р = 95 %:
объема N и доверительной веро-
№ |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1.30 |
0.72 |
0.51 |
0.40 |
0.33 |
0.29 |
0.25 |
0.23 |
0.21 |
0.19 |
P,N |
для проверки результатов наблюдений на наличие
грубых погрешностей в упорядоченной выборке объема N для доверительной вероятности Р = 95 %:
№ |
3 |
4 |
5 |
7 |
10 |
15 |
20 |
30 |
100 |
uP,N |
0.94 |
0.76 |
0.64 |
0.51 |
0.41 |
0.34 |
0.30 |
0.26 |
0.20 |
для проверки элементов выборки на наличие гру-
бых погрешностей по СКО x вероятности Р = 95 %:
в выборке объёма N при доверительной
№ |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
vP,N |
1.15 |
1.46 |
1.67 |
1.82 |
1.94 |
2.03 |
2.11 |
2.18 |
2.23 |
2.29 |
Производные элементарных функций:
Функция |
Производная |
x |
n |
nx |
n−1 |
|
|
eax |
aeax |
a |
x |
a |
x |
ln a |
|
|
ln x |
1 / x |
|
|
sin x |
cos x |
|
|
cos x |
−sin x |
|
|
|
|
|
|
|
|
|
|
Функция
tgx
ctgx
(u + v)
f = f (u (x))
Производная
1 cos2 x
cos2 x
−1 sin |
2 |
|
x |
|
|
|
|
u + v |
|
|
|
|
|
|
|
’ |
|
u v + uv |
|
|
|
(u v + uv ) |
|
v |
2 |
|
|
fx = fuux
Список литературы
1.Савельев И. В. Курс общей физики: В 3 т. Т. 2. Электричество и магнетизм. Волны. Оптика. СПб.: Лань, 2006.
2.Ландсберг Г. С. Оптика. М.: Наука, 1976.
3.Калитеевский Н. И. Волновая оптика. СПб.: Лань, 2010.
4.Морозов В. В., Соботковский Б. Е., Шейнман И. Л. Методы обработки результатов физического эксперимента: учеб. пособие. СПб.: Изд-во СПбГЭТУ
«ЛЭТИ», 2004.
5.Савельев И. В. Курс общей физики в 3 т. Т. 3. Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц. СПб.: Лань, 2007.
6.Барщевский Б. У. Квантово-оптические явления. М.: Высш. шк., 1982.
7.Вертц Дж., Болтон Дж. Теория и практические приложения метода ЭПР. М.: Мир, 1975.
8.Лундин А. Г., Федин Э. И. Ядерный магнитный резонанс. М.: Наука,
1980.
Богачев Юрий Викторович Вяткин Вадим Михайлович Кузьмина Наталья Николаевна Лоскутников Виктор Серафимович Морозов Вениамин Васильевич Шишкина Марина Николаевна
Оптика и атомная физика
Лабораторный практикум
Компьютерная верстка Е. С. Николаевой
Редактор
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
Подписано в печать ??.??.19. Формат 60×84 1/16. Бумага офсетная. Печать цифровая. Печ. л. 7,75.
Гарнитура «Times New Roman». Тираж ?? экз. Заказ .
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
Издательство СПбГЭТУ «ЛЭТИ» 197376, С.-Петербург, ул. Проф. Попова, 5
127


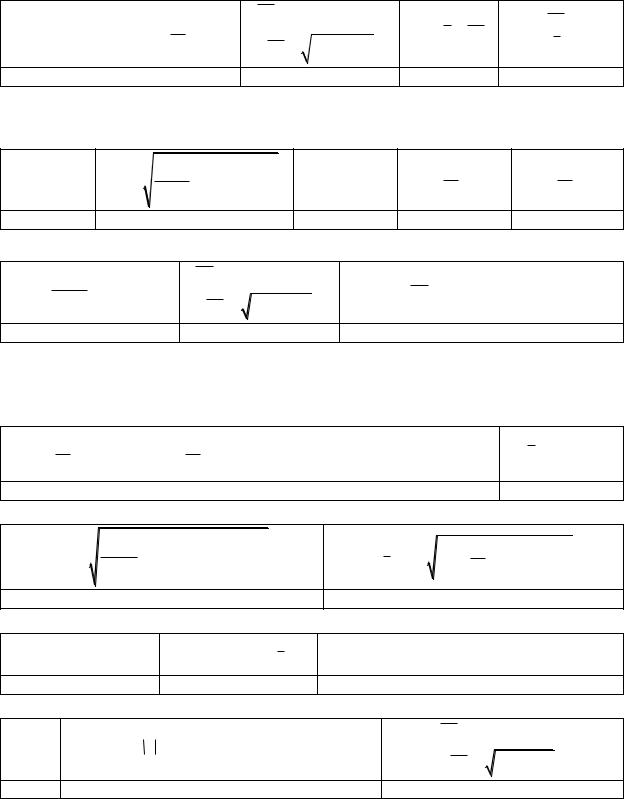


 cos
cos