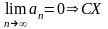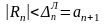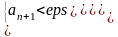Третий семестр (вечерка) / Практика / 4. ТР 2.5 по теме РЯДЫ
.docx
ТР 2.5 по теме «РЯДЫ»
Часть-1. «Числовые ряды». Максимум –8(12) баллов; Зачет > 4 баллов Задание. Для положительных числовых рядов S3 и (S1 и/или S2)
1.1 Выбрать «подходящий» признак сходимости, доказать сходимость ряда и получить оценку суммы остатка ряда. 2 балла 1.2 Определить и найти оценку суммы ряда с заданной точностью ε . 2 балла
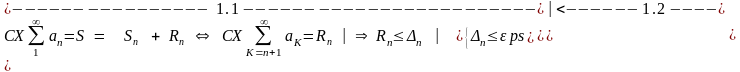
1.1 Признак |
аn=a(n) |
1.1 CX/PX |
1.1 Rn < ∆n |
1.2
|
Интегральный
|
(np) |
|
|
|
Даламбера |
(n!) |
|
|
|
Коши |
|
|
|
|
Лейбница
Знакочередующийся
ряд |
|
|
|
|
=================================================================================
ПРИМЕРы ИССЛЕДОВАНИЯ ЧИСЛОВОГО РЯДА.
Пример 1
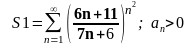
1.1
Для исследования числового ряда
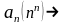 выберем признак Коши:
(а) «
Положительный числовой ряд
выберем признак Коши:
(а) «
Положительный числовой ряд
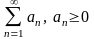 сходится, если
сходится, если
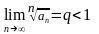 »
(b)
« Для любого q0
∊(q;1)
имеет место оценка суммы остатка
ряда:
»
(b)
« Для любого q0
∊(q;1)
имеет место оценка суммы остатка
ряда:
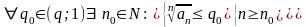
q =
q =
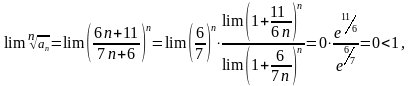
РЯД СХОДИТСЯ → S = Sn + Rn, Rn – сумма остатка ряда.
Для оценки суммы остатка ряда выберем q0 ∊(q;1) ( например, q0= 0.4) и решим неравенство:
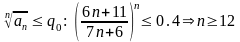
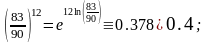
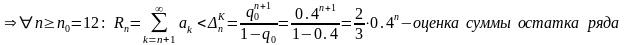
1.2
Для получения оценки суммы остатка
ряда с точностью εps
= 0.001 решим неравенство
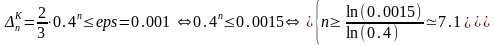
Таким
образом,
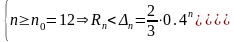
Определим оценку суммы ряда с погрешностью eps = 0.001 как интервал S∊(S12;S12+Δ12)
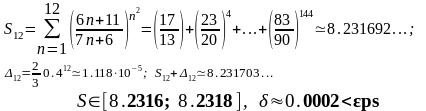
==========================================================================
Пример 2
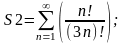
1.1
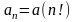
выберем признак Даламбера:
(a)
« Положительный числовой ряд
сходится, если
выберем признак Даламбера:
(a)
« Положительный числовой ряд
сходится, если
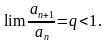 »
(b)
« Для любого q0
∊(q;1)
имеет место оценка суммы остатка
ряда:
»
(b)
« Для любого q0
∊(q;1)
имеет место оценка суммы остатка
ряда:
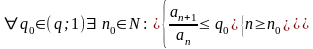
q =
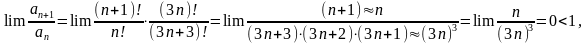
РЯД СХОДИТСЯ →
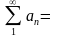 S = Sn
+ Rn,
Rn
– сумма остатка ряда.
S = Sn
+ Rn,
Rn
– сумма остатка ряда.
Для оценки суммы остатка ряда выберем q0 ∊(q;1) ( например,q0=0.5) и решим неравенство:
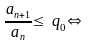
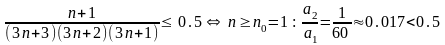
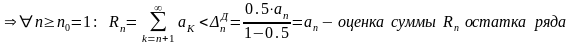 Для получения оценки суммы остатка
ряда с точностью εps
= 0.001 решим неравенство
Для получения оценки суммы остатка
ряда с точностью εps
= 0.001 решим неравенство
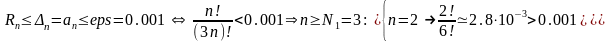
Таким образом,
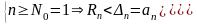
1.2 Определим оценку суммы ряда с погрешностью eps = 0.001 как интервал
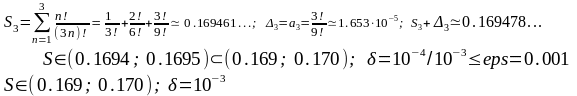
Пример 3
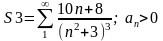
1.1 Так
как
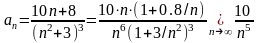 ,
ряд сходится
,
ряд сходится
по интегральному признаку:
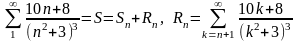
и по интегральному признаку оценка суммы остатка ряда имеет вид:
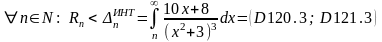
Для упрощения вычислений преувеличим
оценку
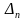 , увеличив числитель дроби:
, увеличив числитель дроби:
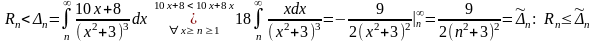
Для получения оценки с точностью
eps=0.001 решим неравенство
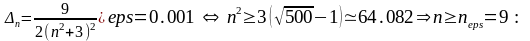
1.2 Определим оценку суммы ряда с погрешностью eps = 0.001 как интервал
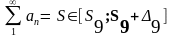
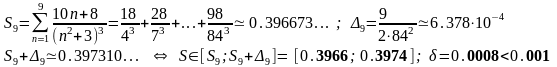
--------------------------------------------------------------------------------------------------------------------------------
Результаты.
1.
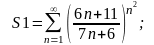 Пр.
Коши→q0= 0.4
Пр.
Коши→q0= 0.4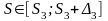 =
=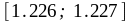
2.
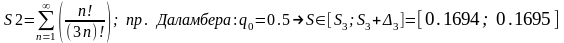
3.
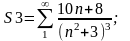 Интегральный
пр.
Интегральный
пр.
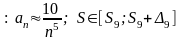 =
=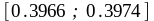

 →
S∊(*;**)
→
S∊(*;**)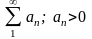
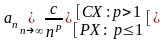
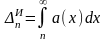
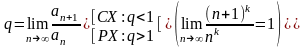

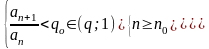
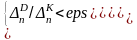
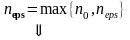
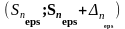
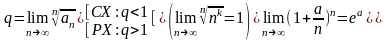
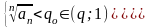
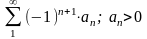
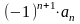 an>0
an>0