Третий семестр (вечерка) / Лекции / 7. Тригонометрическая система функций и тригонометрический ряд Фурье

Тригонометрическая система функций и тригонометрический ряд Фурье,

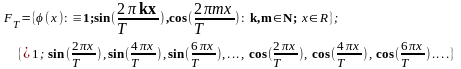(1)

Свойства функций множества F:

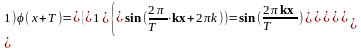
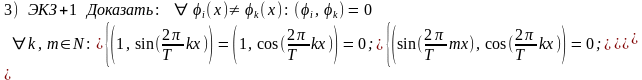
Тригонометрическим рядом по тригонометрической системе 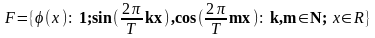называется функциональный ряд вида

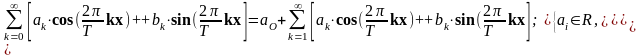(2)

Следствия. 1) Частичные суммы ряда являются тригонометрическими многочленами:

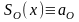
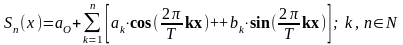
2) Если ряд (2) сходится, его сумма S(x) определяет периодическую функцию с периодом «Т».

--------------------------------------------------------------------------------------------------------------------------------------

Представление функции на отрезке тригонометрическим рядом Фурье.

Пусть функция f(x) интегрируема (кусочно-непрерывна) на [a;a+Т] и имеет место равенство

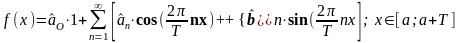(3)

Умножим последовательно обе части равенства (3) на φ(x)∊F и проинтегрируем от а до а+Т:

-----------------------------------------------------------------------------------------------------------------------------------------

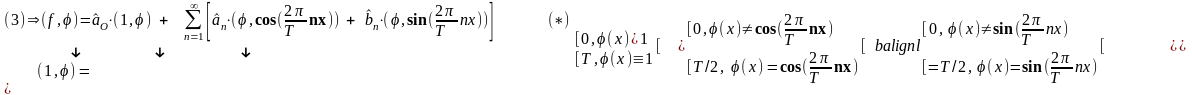
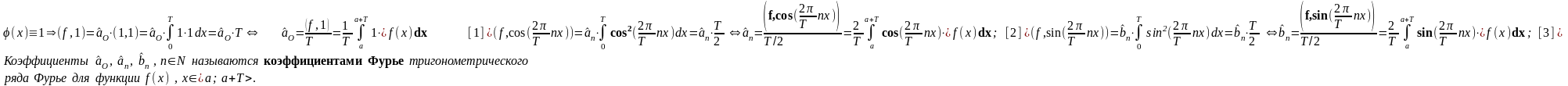Теорема Дирихле (Поточечная сходимость тригонометрического ряда Фурье).

«Если функция f(x) кусочно-непрерывна и ограничена на [a; a+Т], то тригонометрический ряд Фурье 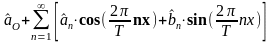с коэффициентами [1-3] (1) сходится на промежутке [a; a+T] к функции f(x) «в среднем»:

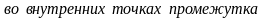- его сумма 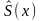равна полусумме односторонних пределов функции f(x) в точке

-

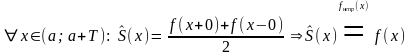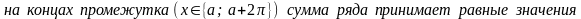
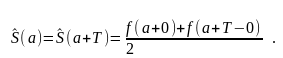
(2) сходится на всей числовой оси 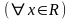и определяет в R периодическую функцию ( сумму ряда) с периодом «T»:

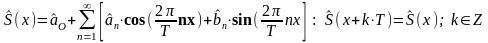
(3) Частичная сумма ряда 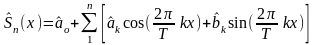определяет тригонометрический многочлен наилучшего среднеквадратического приближения функции f(x) на промежутке [a; a+T] :

Среднеквадратическое отклонение (СКО) этого многочлена от функции f(x) на [a; a+T]

СКО=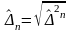 определяется рекуррентными соотношениями:

=====================================================================

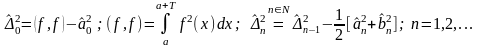
ПРИМЕР

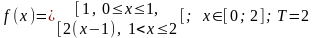
Тригонометрический ряд Фурье 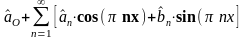с коэффициентами

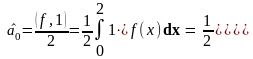
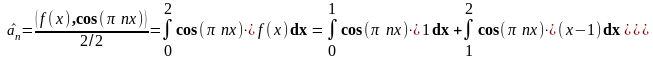
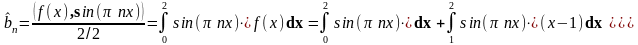
По теореме Дирихле :

Тригонометрический ряд Фурье

(1) сходится на промежутке [0; 2] к функции f(x) «в среднем»: 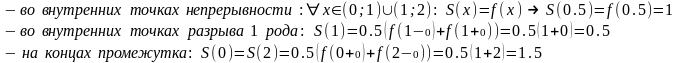(2) ⇒ S(-3)=S(-3+2∙2)=S(1)=0.5; S(14)=S(0+7∙2)=S(0)=1.5; S(2,5=0.5+2)=S(0.5)=f(0.5)=1;

График суммы ряда y=S(x):

ЭКЗ +1 для функции G(x)=x² на [0;1]

1) Записать тригонометрический ряд Фурье, определить коэффициенты Фурье.

2) Изобразить по т. Дирихле график суммы ряда Фурье y=S(x), x∊[-1;3] и вычислить S(0), S(0.5), S(1), S(- 3.2).