
Третий семестр (вечерка) / Лекции / 6. Глава числовые ряды 3-4
.docx
§2 Свойства и алгоритм исследования числового ряда.
Числовой ряд
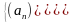
Из определения (1) и представления числового ряда в виде
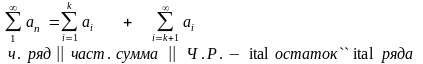
следует СВОЙСТВО: « числовой ряд и остаток ряда сходятся и расходятся ОДНОВРЕМЕННО !!». (2)
АЛГОРИТМ исследования числового ряда : [I] →[II].
[I] Установить
сходимость или расходимость ряда:
-
либо по определению (1),
- либо используя
«признак СХ/РХ числового ряда».
1.1
Необходимый (но НЕ достаточный)
признак сходимости ряда:
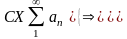
Достаточный признак
расходимости:
(3)
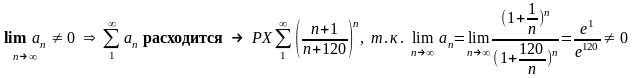
1.2 Признак «сравнения» положительных рядов.
Из МА: «Монотонно
возрастающая и ограниченная СВЕРХУ
функция имеет предел»: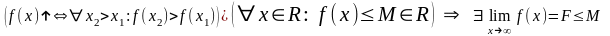 (**)
(**)
Пусть
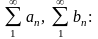 an>bn>0
an>bn>0
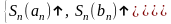
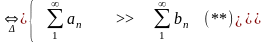 Пусть
Пусть
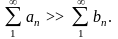 Из определений (1) и (**) следует
Из определений (1) и (**) следует
Теорема (Признак «сравнения»
положительных рядов).
1)
«Если ряд
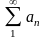 сходится
сходится сходится ряд
сходится ряд
 и его сумма
ограничена СВЕРХУ:
S(bn)
< S(an).
и его сумма
ограничена СВЕРХУ:
S(bn)
< S(an).
2) «Если ряд
 расходится,
расходится и ряд
расходится,
расходится и ряд

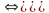 [I]
→[II]
Для сходящегося ряда
[I]
→[II]
Для сходящегося ряда
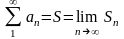 найти
«оценку суммы ряда
найти
«оценку суммы ряда
с заданной погрешностью εps>0»
⇔ интервал
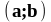 :
:

Оценку суммы сходящегося ряда в виде интервала получают на основании определения (1) и свойства (2):
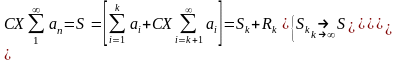
Например, если положительный ряд
сходится

и найдена оценка
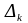 суммы
его остатка
суммы
его остатка
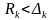 ,
оценка суммы ряда имеет вид:
,
оценка суммы ряда имеет вид:
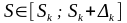 ,
при этом
,
при этом
- все вычисления выполняются «в полной разрядной сетке»,
- левый конец интервала
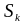 округляется
«по недостатку»,
округляется
«по недостатку»,
- правый конец интервала
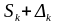 округляется
«по избытку»:
округляется
«по избытку»:
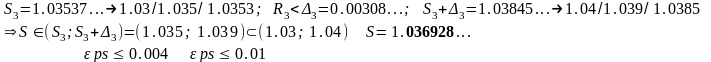
§3 Признаки Даламбера и Коши сходимости положительного ряда.
Рассмотрим для положительного числового
ряда
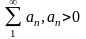 два
предела при n→∞:
- предел
отношения последующего члена ряда к
предыдущему
два
предела при n→∞:
- предел
отношения последующего члена ряда к
предыдущему
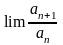 и
- предел арифметического корня
lim(
и
- предел арифметического корня
lim(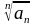 ).
).
Теоремы(признаки Даламбера и Коши).
«Если для положительного ряда
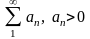 существует
при n→∞ предел
существует
при n→∞ предел
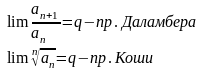 ТО ч. ряд
ТО ч. ряд
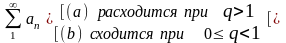
Док-во теорем основано на определении предела функции

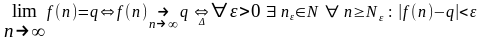 ,
,
на достаточном признаке расходимости
ряда (lim(an)≠0
⇨ РХ
)
и на признаке
«сравнения»
положительных рядов
(а)
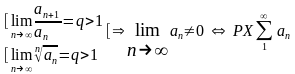
 (b)
Пусть
(b)
Пусть
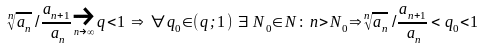
 ⇔n
≥ N0
⇔n
≥ N0
q q0
ПРИЗНАК Даламбера ↓↓ || || Признак Коши ↓↓
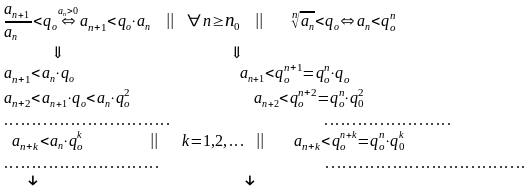
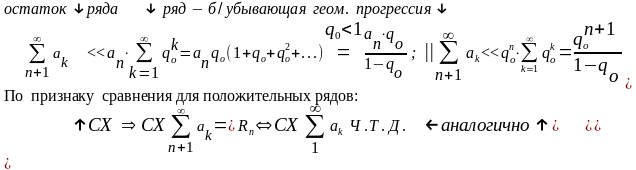
Таким образом,
если
 положительный
ряд
сходится
и для
любого qo∊(q;1)
имеют место
ОЦЕНКИ
суммы Rn
остатка ряда и
суммы ряда S:
положительный
ряд
сходится
и для
любого qo∊(q;1)
имеют место
ОЦЕНКИ
суммы Rn
остатка ряда и
суммы ряда S:
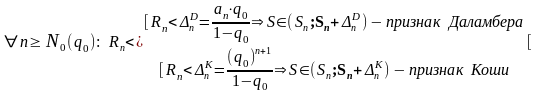
Замечания.
1.
Признак
Даламбера предпочтителен для рядов,
общий член которых
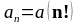 содержит
факториалы.
содержит
факториалы.
2.Признак
Коши предпочтителен для рядов, общий
член которых содержит показательные
функции
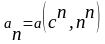 .
3. Признаки
Даламбера
и
Коши «не
работают» для рядов со степенной
зависимостью
.
3. Признаки
Даламбера
и
Коши «не
работают» для рядов со степенной
зависимостью
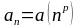 ,
для которых
,
для которых
q=1:
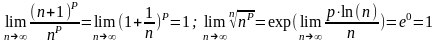
Примеры.
1)


2)

3)
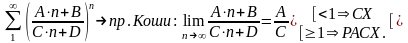
4)
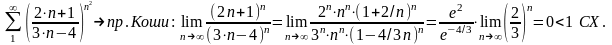
§4 Интегральный признак сходимости. Интегральная оценка суммы ряда.
Рассмотрим
положительную числовую последовательность
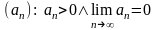 ,
положительную числовую функцию a(x):
a(x=n∊N)=an,
x∊[1;∞)
и соответствующие им
числовой ряд
и
несобственный интеграл
,
положительную числовую функцию a(x):
a(x=n∊N)=an,
x∊[1;∞)
и соответствующие им
числовой ряд
и
несобственный интеграл
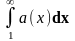 .
.
Теорема (интегральный признак сходимости/расходимости положительного ряда).
«Положительный
числовой ряд
:
(1)
сходится и расходится одновременно
с
несобственным интегралом
,
(2)
для сходящегося ряда
 имеют
место
- «интегральная оценка» суммы
остатка ряда
имеют
место
- «интегральная оценка» суммы
остатка ряда
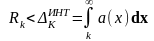 и
- «интегральная
оценка» суммы ряда
и
- «интегральная
оценка» суммы ряда
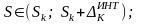
Док-во теоремы (+1) следует из сравнения на промежутках [1;n] и [n;∞) площадей криволинейной трапеции SKT (0≤ у ≤ а(х)), вписанной SВП и описанной SОП ступенчатых фигур, образованных прямоугольниками высотой h=aК и шириной ∆k = 1, k∊N:
[1;n]:
SОП
=
a1+a2+..+an-1
= Sn-1
>SKT
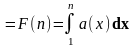 >
SВП
=
a2+a3+..an
=
Sn
-
a1,
(1)
[n;∞):
SKT
>
SВП
=
a2+a3+..an
=
Sn
-
a1,
(1)
[n;∞):
SKT
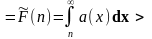 SВП
SВП
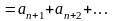 (2)
(2)
a(x)

a1
an-1


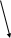

a2
an
an+1


x
n
1
2
3
n-1
n+1

