
Третий семестр (вечерка) / Лекции / 4. Операторный метод анализа электрической цепи (ТОЭ)
.docx[I] Операторный метод анализа электрической цепи (ТОЭ):
E = сonst– «электродвижущая сила»(ЭДС) - напряжение источника тока; i(t) – ток в цепи; UR(t), UC(t), UL(t) – напряжения в цепи на резисторе «R», на конденсаторе «С» и на катушке индуктивности «L»
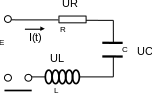
UR(t)
=i(t)∙R;
UC(t)
=UC(0)+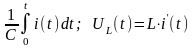
Закон Ома для замкнутой R,C,L – цепи с Э.Д.С.= E=const : E=UR+UC+UL
(1) Пусть в начальный момент t=0: UC(0)=0; i(0)=0 В этом случае ток в цепи i(t) определяется уравнением:
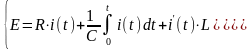 (1)
(1)
(2)
Полагая, что i(t)
– оригинал, после
преобразования
Лапласа:
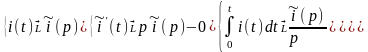
получим
алгебраическое
уравнение для изображения тока в цепи
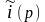
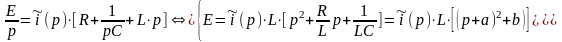 (2)
(2)
(3) Решение уравнения (2) определяется параметром “b” электрической цепи :
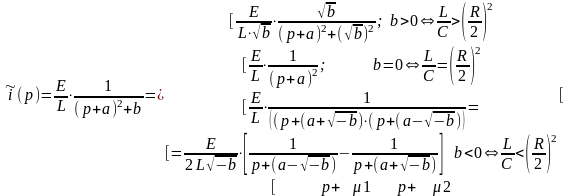 (3)
(3)
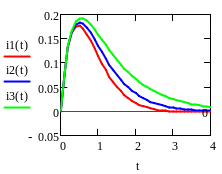
(4) Обратное преобразование Лапласа восстанавливает решение дифференциального уравнения (1) – ЗАКОН ИЗМЕНЕНИЯ ТОКА В ЦЕПИ в зависимости от соотношений между параметрами R,L,C цепи:
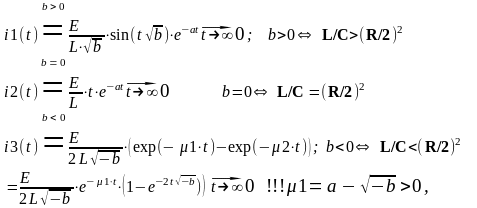 (4)
(4)
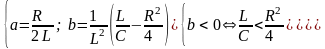
Например,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
[II]
Переходный процесс в RL-
эл. цепи: E
= i(t)∙R
+ I’(t)∙L
∧i(0)=0
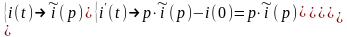
 E=U=const
E=U=const
Переходный процесс в RL-цепочке↑
------------------------------------------------------------------------------------------------------------------------------
RL - эл. цепь с нулевыми начальными усуловиямиi(t)=(E/R) (1-exp(-Rt/L)); i'(tii’(t)=(E/L)exp(-Rt/L); UR=iR=E (1-exp(-Rt/L); UL=i'L=Eexp(-Rt/L)
![]()
![]()
![]()
![]()
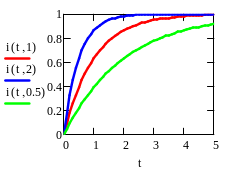
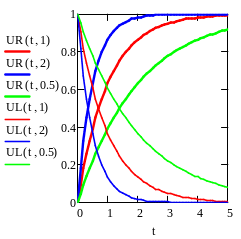
UR(t)+UL(t)=const
[III] Законы Кирхгофа: 1) Алгебраическая сумма токов в любом «узле» цепи равна нулю. 2) В любом замкнутом контуре цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжения на всех резистивных элементах этого контура.


