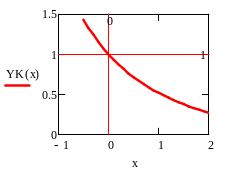
Третий семестр (вечерка) / Лекции / 3. Параграф 8. НЛДУ-2 с постоянными коэффициентами. Метод «вариации постоянных»
..docx
§8 НЛДУ-2 с постоянными коэффициентами. Метод «вариации постоянных».
ИЗВЕСТНО:
(1)
Алгоритм
метода «вариации постоянной» для НЛДУ-1:
y’(x)+a(x)y(x)=g(x)
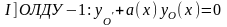 -ДУРП
yO(x,C)
= C∙φO(x)
– общее
решение ОЛДУ
II]
Общее решение НЛДУ-1 находится методом
«вариации постоянной».
-ДУРП
yO(x,C)
= C∙φO(x)
– общее
решение ОЛДУ
II]
Общее решение НЛДУ-1 находится методом
«вариации постоянной».
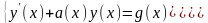
(2)
Общее решение ОЛДУ-2
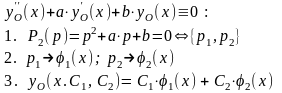 =============================================================================
=============================================================================
Рассмотрим НЛДУ-2 с постоянными коэффициентами
y’’(x)+a∙y’+b∙y=f(x) – НЛДУ-2 (1)
Рассмотрим метод «вариации постоянных» нахождения общего решения НЛДУ-2.
АЛГОРИТМ метода «вариации постоянных» нахождения общего решения НЛДУ-2.
[I]
По корням
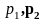 характеристического
полинома ЛДУ-2
(1.)
находятся
частные
решения
характеристического
полинома ЛДУ-2
(1.)
находятся
частные
решения
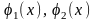 ОЛДУ (2.)
и
его
общее
решение
ОЛДУ (2.)
и
его
общее
решение
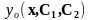 : 1.→2.→
3.
: 1.→2.→
3.
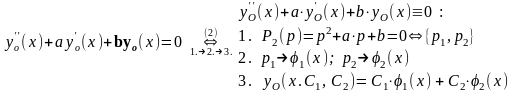 (2)
(2)
[II Решение НЛДУ-2 (1) ищется в виде
y(x)=
C1(x)∙φ1(x)+
C2(x)∙φ2(x)
(3)
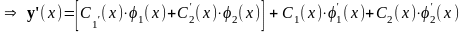
Поскольку искомая функция y(x) «связана» одним уравнением (1), а выражается через две функции (3), наложим на эти дифференцируемые функции дополнительное условие
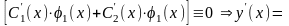
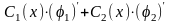 (4)
(4)
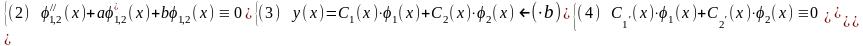
После подстановки (3) в НЛДУ (1) с учётом (2) и (4)
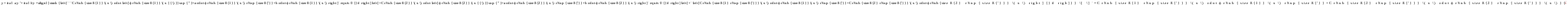
для функций С1'(х) и С2'(х) получим Систему Линейных Алгебра Уравнений (СЛАУ):
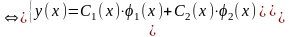
Таким образом, общее решение НЛДУ-2 :
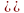
ПРИМЕР.
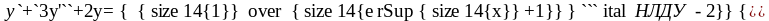
 [II]
Общее
решение НЛДУ-2
[II]
Общее
решение НЛДУ-2
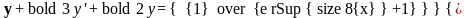 10.342
10.342
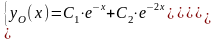
Решение
СЛАУ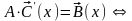
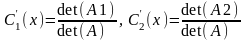
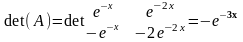
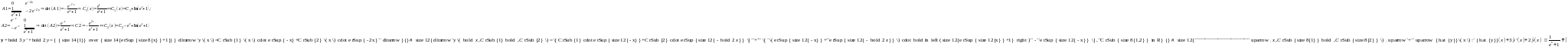 Замечания.
1)
Общее
решение НЛДУ представляет аддитивную
сумму общего решения
Замечания.
1)
Общее
решение НЛДУ представляет аддитивную
сумму общего решения
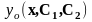 соответствующего
ОЛДУ и частного решения
соответствующего
ОЛДУ и частного решения
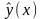 НЛДУ
.
2) Решение задачи Коши
НЛДУ
.
2) Решение задачи Коши
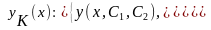
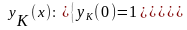
y"(x) + 3y'(x) +2y(x) = 1/(ex+1) p2 +3p +2=(p-1)(p-2)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
---------------------------------- --------------------------------------------------------------------------
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()