
Третий семестр (вечерка) / Лекции / 2. Дифференциальные уравнения 1. ИДЗ 2, формулировка
.docx
ДУ-1: 1) F[x,y(x),y’(x)/dy(x)]=0
∧
x∊Dx
∧
y∊Dy
→2) Множество решений →3)Решение задачи
Коши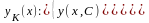
[I] ДУ-1 с
разделёнными переменными
f(y)dy
= g(x)dx
∧
x∊Dg
∧
y∊
Df
→ 2)
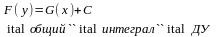 →3)
→3)
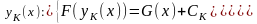
[II] ДУ с Разделяющимися Переменными (ДУРП).
M1`(x)N1(y)dy=
M2`(x)N2(y))dx
∧x∊Dx∧y∊Dy
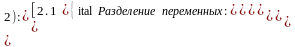
[III] Неоднородные Линейные ДУ-1(относительно y(x) и y’(x)/dy(x)):
(1) y’(x)+b(x)y(x)=f(x) ⇨dy(x)+b(x)∙y(x)dx= f(x)dx
2) 2.1 ОЛДУ-1:
yо’(x)+b(x)yо(x)=0
ДУРП
yо(x,C)=C∙φo(x):
φo’(x)+b(x)∙φo(x)=0
2.2 НЛДУ-1(метод
«вариации постоянной»).
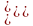
3)
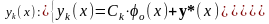
[IV]
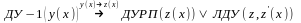
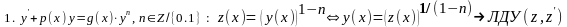
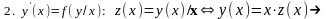 ДУРП(z(x))
ДУРП(z(x))
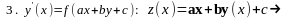 ДУРП(z(x))
ДУРП(z(x))
ИДЗ-2 по теме «Дифференциальные уравнения первого порядка» ДУ-1. Задание. Для каждого из ДУ 1) и 2)
1.1 указать тип ДУ и найти множество его решений ;
1.2 найти решение задачи Коши с заданным условием y(x0)=y0 ДУ-3 привести к ДУРП или ЛДУ подходящей заменой функции.
