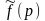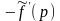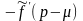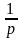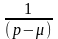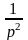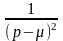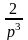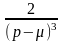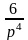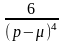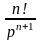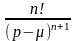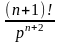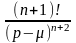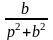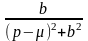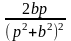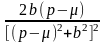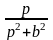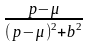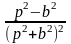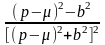Третий семестр (вечерка) / Лекции / 1. Таблица операционных соответствий и операционное исчисление
.docx
Таблица
операционных соответствий
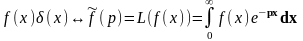
|
f(x)[δ(x)] 1 |
L[f(x)]= 2
=
|
L[eμx∙f(x)] 3 p→p-μ |
L[x∙f(x)]= 4
= |
L[eμx∙x∙f(x)]= 5
= |
1 |
1 |
|
|
|
|
2 |
x |
|
|
|
|
3 |
x2 |
|
|
|
|
4 |
xn |
|
|
|
|
5 |
eμx |
|
|
|
|
6 |
sin(bx) |
|
|
|
|
7 |
cos(bx) |
|
|
|
|
СВОЙСТВА ОПЕРАЦИОННЫХ СООТВЕТСТВИЙ (теоремы операционного исчисления)
1.
Линейность:
L[c1f1(x)
+ c1f1(x)]
↔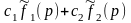
2.
Т.
смещения: f(x)∙eμx
∙δ(x)
↔
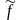 (p-μ)
(p-μ)
3.
Т.
запаздывания:
f(x-
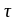 )∙
)∙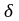 (x-
)
(x-
)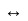
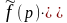 e
e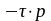
4.
Дифференцирование
оригинала:
(f(x))’
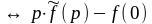 5.
Дифференцирование
изображения:
(x)∙f(x)
5.
Дифференцирование
изображения:
(x)∙f(x)
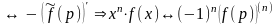
6.
Свертка
оригиналов:
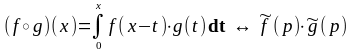
7.
Интегрирование
оригинала:
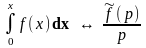
В Таблице изображения оригиналов представляют правильные рациональные дроби (ПРД).
Алгоритм восстановления оригинала по его дробно-рациональному изображению: а) разложение ПРД на простейшие; б) приведение слагаемых разложения к «табличному виду» c учётом т.смещения и т. запаздывания и в) восстановление оригинала по ТОС.
ИДЗ-1 по теме «Операционное Исчисление».
Вар. |
1) |
2) |
3) f(x) |
4) f(x) |
«Задание».
1) Найти оригинал f(x) по его дробно-рациональному изображению . 2) Найти оригинал f(x) по его изображению , используя ТОС и теоремы смещения и запаздывания.
3) Изобразить график y=f(x), записать аналитический вид функции-оригинала f(x) и найти его изображение.
4)
Вычислить несобственный интеграл
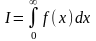 ,
определив
его как значение изображения оригинала
g(x)
в
точке :
,
определив
его как значение изображения оригинала
g(x)
в
точке :
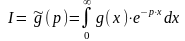 .
.