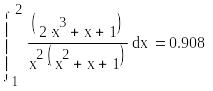Второй семестр (вечерка) / Практика / 9. Правильная рациаональная дробь и полиномы
.doc
[I]
Полином степени n:
(0)
![]() (1)
(1)
Два
полинома тождественно равны (![]() ,
если равны их коэффициенты при одинаковых
степенях х.
Например,
,
если равны их коэффициенты при одинаковых
степенях х.
Например,
![]()
(1)
В
С:![]() -
полином степени n
имеет
ровно n
корней,
среди которых могут быть равные (кратные).
-
полином степени n
имеет
ровно n
корней,
среди которых могут быть равные (кратные).
(2)
![]() (2)
представляется
в виде произведения, в котором корню
(2)
представляется
в виде произведения, в котором корню
![]() кратности r
соответствует множитель (x-a)r.
кратности r
соответствует множитель (x-a)r.
(3)
Следствие. (Теорема Виета)
 (3)
(3)
Целые
корни
![]() полинома
полинома
![]() с
целыми
коэффициентами
с
целыми
коэффициентами
![]() являются
делителями
коэффициента с0
(«угадывание»
целых корней полинома):
являются
делителями
коэффициента с0
(«угадывание»
целых корней полинома):
![]()
(4)
В R:
корни
полинома
с вещественными коэффициентами
![]() -
либо вещественные числа
-
либо вещественные числа
![]() ,
либо
попарно-сопряженные
комплексные корни:
,
либо
попарно-сопряженные
комплексные корни:
![]() (4)
(4)
В представлении (2)
-
однократному вещественному корню
![]() соответствует множитель
(x-a);
соответствует множитель
(x-a);
-
к-кратному вещественному
корню
![]() множитель
(x-b)k
;
множитель
(x-b)k
;
- паре комплексно сопряженных корней x1,2=α ± j∙β кратности k ≥ 1 соответствует множитель – квадратный трехчлен с отрицательным дискриминантом
![]()
![]()
[II] Рациональная
дробь
(РД)
![]()
Правильная ПРД: n<m; неправильная НРД:
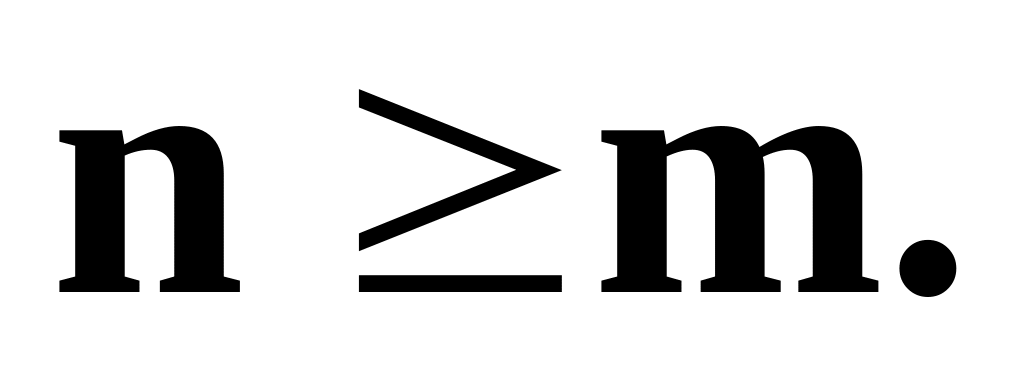
(5) Неправильная рациональная дробь делением полинома числителя на полином знаменателя («уголком») приводится к сумме полинома («частное») и соответствующей правильной рациональной дроби:
 (5)
(5)

(6) ПРД представляется в виде суммы «простейших РД» вида
![]() ;
;
В
разложении правильной рациональной
дроби
 на простейшие
- множителю (x-a)
(однократному
корню)
знаменателя Qm(x)
соответствует слагаемое
на простейшие
- множителю (x-a)
(однократному
корню)
знаменателя Qm(x)
соответствует слагаемое
![]() ;
;
- множителю(x-b)r (r-кратному корню), r>1 знаменателя Qm(x) соответствуют “r” слагаемых
![]() ;
;
-
множителю (x2+px+q),
D<0
знаменателя
Qm(x)
соответствует слагаемое
![]() ;
;
- множителю (x2+px+q)r , r>1, D<0 знаменателя Qm(x) соответствуют “r” слагаемых
![]()
Алгоритм
нахождения коэффициентов разложения
ПРД на простейшие:
(a)
по знаменателю Qm(x)
ПРД
![]() записывается
разложение на простейшие
с
неопределёнными коэффициентами
А,Bk,Mk,Nk;
записывается
разложение на простейшие
с
неопределёнными коэффициентами
А,Bk,Mk,Nk;
(b)
сумма простейших приводится к общему
знаменателю
![]() ;
;
(c)
коэффициенты разложения находятся из
условия равенства коэффициентов
полиномов Pn(x)
и
![]() при
одинаковых степенях “xk”,
k=0,1.2,…,n
решается
СЛАУ (n+1
уравнений с n+1
неизвестными).
при
одинаковых степенях “xk”,
k=0,1.2,…,n
решается
СЛАУ (n+1
уравнений с n+1
неизвестными).
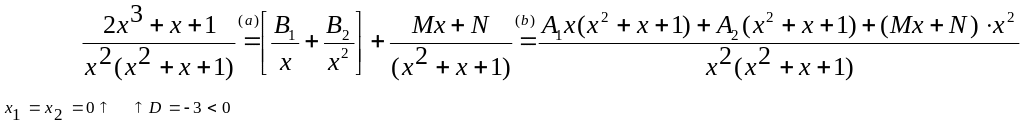

Замечание. Коэффициент
А, соответствующий
множителю (х-а),
и коэффициент
Вr
,
соответствующий множителю (х-b)r
знаменателя
Qm(x),
можно
вычислить до решения СЛАУ по формулам:
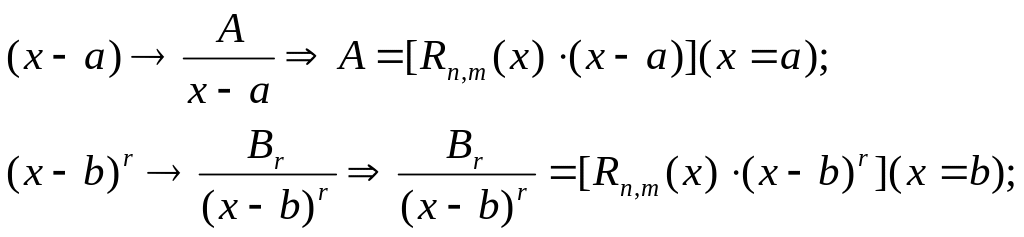
==========================================================================
Типовой расчёт ТР-2.3 по теме «Интегрирование рациональныхдробей».
Задание.
1.
Выделить
целую
часть НРД,
разложить
на
простейшие соответствующую ПРД,
найти
неопределённый
интеграл
![]()
2.
Разложить
РД
на простейшие и
найти
неопределённый
интеграл
![]()
3.
Разложить
РД
на простейшие,
найти
неопределённый
интеграл
![]() и
и
вычислить
определённый
интеграл
![]() по
формуле Ньютона-Лейбница:
по
формуле Ньютона-Лейбница:
![]()
![]()