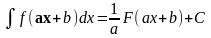Второй семестр (вечерка) / Практика / 8. Практика по неопределенному интегралу
.docx
[I] ТАБЛИЦА ПЕРВООБРАЗНЫХ, НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.
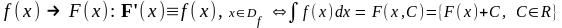
f(x) |
|
f(x) |
|
1. xa a¹-1 1,
x,
|
xa+1/(a+1); x,x2/2,
|
8. 1/sin(x) |
ln(ïtg(x/2)ï) |
2. 1/x |
ln(|x|); x∊R\{0} |
9. 1/cos(x) |
ln(ïtg(x/2+p/4)ï) |
3. ax ; a>0 ex |
ax/ln(a) ex |
10.
|
|
4. sin(x) |
- cos(x) |
11.
|
|
5. cos(x) |
sin(x) |
12.
|
|
6. 1/cos2(x) |
tg(x) |
13.
|
|
7. 1/sin2(x) |
-ctg(x) |
14.f(t)
→F(t)
⇒
|
|
[II] Г.Б. Двайт «ТАБЛИЦА ИНТЕГРАЛОВ и другие математические формулы», М. ,Наука, 1977
[III] Приведение к «табличному виду»: Метод «замены переменной»:
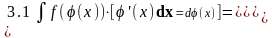
[IV]
Приведение к «табличному виду»: Метод
«интегрирования по-частям»:
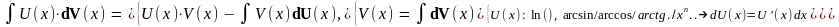
ОТТ - Основные Тригонометрические Тождества:
0) sin2(x)+ cos2(x)=1; d(sin(x))=cos(x)dx; d(cos(x)= -sin(x)dx;
1) 1+tg2(x)=1/cos2(x); d(tg(x)=dx/cos2(x); 1+ctg2(x)=1/sin2(x); d(ctg(x)= - dx/sin2(x);
2) sin2(x)=0.5( 1- cos(2x) ); cos2(x)=0.5( 1+cos(2x))
3) 2sin(x)cos(x)=sin(2x); cos(2x) = cos2(x)-sin2(x) = 2cos2(x)-1 = 1-2sin2(x)
ПРАКТИКА: «Таблица первообразных. Неопределённый интеграл».
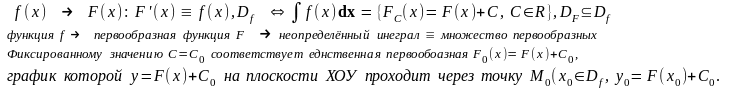 ЭКЗ.
Для заданной функции f(x) найти : 1)
множество первообразных FС (x); 2)
первообразную F0(x), удовлетворяющую
началь-
ному условию: F0(x0∊DF)=y0.
ЭКЗ.
Для заданной функции f(x) найти : 1)
множество первообразных FС (x); 2)
первообразную F0(x), удовлетворяющую
началь-
ному условию: F0(x0∊DF)=y0.
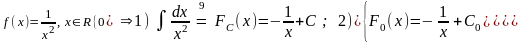
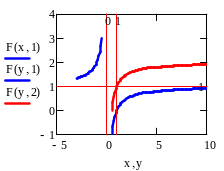
M0(1,1)⇒∃!
F0(x)=2-1/x;
x>0;
FС
(x)=C - 1/x ; C∊R;
x<0 ∧
x>0
1. «
Табличное интегрирование» :
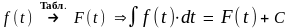
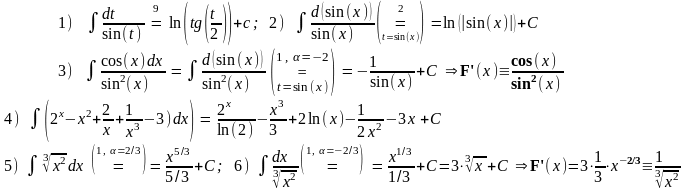
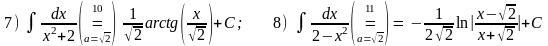
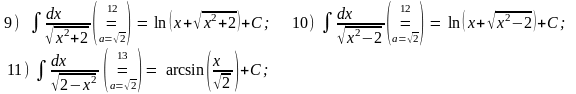
2.
«Расширение» таблиц:
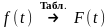 ⇒
⇒
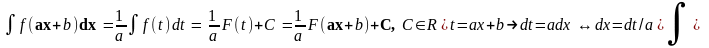
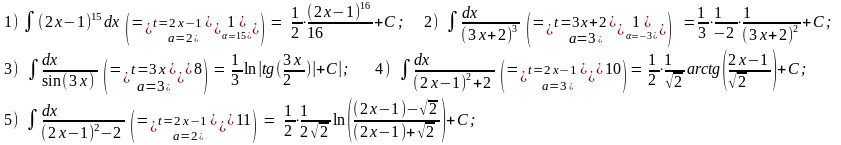
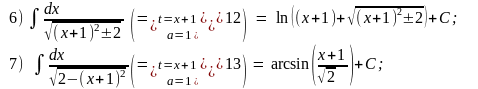
Выделение полного квадрата в квадратном трёхчлене: x2+bx+c= (x+b/2)2- b2/4 +c
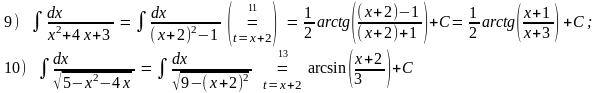
3. Приведение к табличному виду: метод «замены переменной».
3.1
«Подведение под знак
дифференциала»:
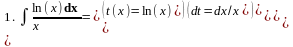
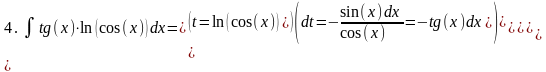
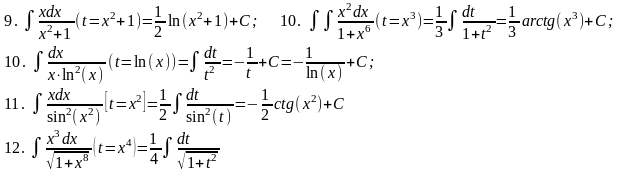
3.2 Приведение к табличному виду: «Метод подстановки»:
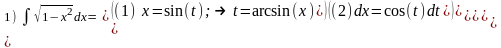
4.
Приведение
к табличному виду: метод
«интегрирования по частям».
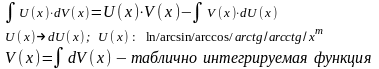
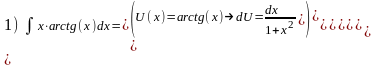
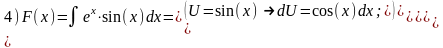
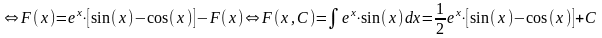
КР-3 по теме «Первообразная и неопределённый интеграл».
Задание. Для каждого примера:
1)
Найти неопределённый интеграл
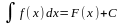 ,
используя методы «замены переменной»,
«интегрирования по частям», таблицу
первообразных и тригонометрические
тождества.
2) Доказать тождество
F’(x)≡f(x).
,
используя методы «замены переменной»,
«интегрирования по частям», таблицу
первообразных и тригонометрические
тождества.
2) Доказать тождество
F’(x)≡f(x).

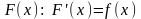
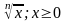
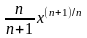
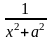
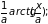 a≠
0
a≠
0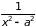
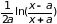 ;
a≠
0
«двухэтажный
логарифм»
;
a≠
0
«двухэтажный
логарифм»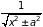
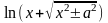 ;a≠0
«длинный
логарифм»
;a≠0
«длинный
логарифм»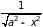
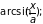 a≠
0
a≠
0