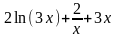Второй семестр (вечерка) / Практика / 3. Типовой расчет 2 часть 1 (2)
.docx
ТР-2.2 «Исследование функции и построение её графика».
[Часть I]. Функция
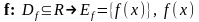 :
1.1 Найти область определения
:
1.1 Найти область определения
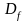 .
Установить четность / периодичность
функции.
1.2 Указать интервалы
непрерывности и точки разрыва
функции.
(1.3) Найти корни и интервалы
знакопостоянства функции.
1.4 Найти
прямолинейные асимптоты графика функции.
.
Установить четность / периодичность
функции.
1.2 Указать интервалы
непрерывности и точки разрыва
функции.
(1.3) Найти корни и интервалы
знакопостоянства функции.
1.4 Найти
прямолинейные асимптоты графика функции.
1.1 Известно, что:

Указать и изобразить на Числовой Прямой область определения заданной функции:
f(x) |
Df |
|
x(x-3)(x+3)>0
|
|
|
|
график симметричен относительно прямой х=-1. |
|
x>0 |
1.2 Известно, что:
1) “Элементарные функции, их сумма, произведение, отношение и композиция непрерывны во внутренних точках области определения:

 2) В точке разрыва х=ар не
выполняется хотя бы одно из условий
1,2,3 непрерывности:
2) В точке разрыва х=ар не
выполняется хотя бы одно из условий
1,2,3 непрерывности:
 Точками
разрыва элементарных функций могут
быть «граничные точки» области
определения.
Точками
разрыва элементарных функций могут
быть «граничные точки» области
определения.
 f
непрерывна на (-∞;-1)U(-1;+∞);
АЛЕВ(-1)=АПР(-1)
= (0-∞)= - ∞ ∧ х=-1∉Df
⇒ хр=-1
точка разрыва 2 рода:
f
непрерывна на (-∞;-1)U(-1;+∞);
АЛЕВ(-1)=АПР(-1)
= (0-∞)= - ∞ ∧ х=-1∉Df
⇒ хр=-1
точка разрыва 2 рода:

1.3 Известно, что:
«Интервалами знакопостоянства (f(x)>0; f(x)<0) являются интервалы между «соседними»
«критическими точками» - корнями f(x)=0 и/или точками разрыва функции. «Знак» функции (+/-) на интервале определяется «знаком f(x*)» в любой точке x* интервала.
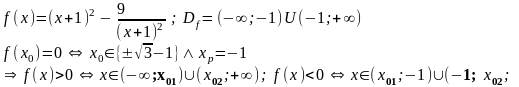
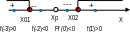
1.4 Известно, что:
1) «Если
 прямая хАС=а называется
«вертикальной асимптотой»
графика функции СЛЕВА/СПРАВА.
прямая хАС=а называется
«вертикальной асимптотой»
графика функции СЛЕВА/СПРАВА.
2) «Если
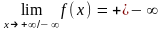 и
существуют конечные пределы
и
существуют конечные пределы
 ,
прямая
yAC
= kx+b
называется «прямолинейной
асимптотой» графика функции на
+/-∞.
,
прямая
yAC
= kx+b
называется «прямолинейной
асимптотой» графика функции на
+/-∞.
 является
левой и правой вертикальной асимптотой
графика y=f(x).
является
левой и правой вертикальной асимптотой
графика y=f(x).
 «прямолинейных
асимптот» на +/-∞ график не имеет.
«прямолинейных
асимптот» на +/-∞ график не имеет.
Результаты ТР-2.2; часть I.
Вар. 28: f(x)=
1.1 f: Df= ; График y=f(x) симметричен относительно прямой х=-1.
1.2 f непрерывна
на (-∞;-1)U(-1;+∞); хр=-1
точка разрыва 2 рода:
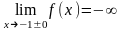
1.3

1.4 График y=f(x)
имеет вертикальную асимптоту хАС = -1;


SOS!!!
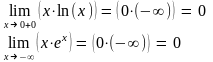


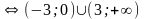

 ;
f(-x)=f(x)
– чётная
;
f(-x)=f(x)
– чётная
 ;
;