
Первый семестр / Лекции ФЭЛ вечерка МУС К.Ф. / Множества и комплексные числа / Глава I-1
.pdf
1
Глава I “ МНОЖЕСТВА”.
§1 Символика и операции.
Понятие множества (синонимы- совокупность, система, набор …) является исходным (аксиома-
тическим) понятием.
Запись A={a:F(a)} –множество «A» элементов «a», удовлетворяющих «условию принадлежности F(a) ». Для числовых множеств F(a):перечисление элементов, формула , уравнение, неравенство, их системы. Множество может быть пустым (не содержит ни одного элемента), конечным и бесконечным, упорядоченным и неупорядоченным.
Пустое множество обозначают символом .
Пусть A={a:F(a)}. Символы " "/" "обозначают принадлежность/непринадлежность
элемента множеству: F(B) b A - «bпринадлежит(является элементом) A»; F(C) C A - «c не принадлежит(не является элементом) множества A». Элементами множества в курсе могут быть
числа, векторы, матрицы, функции, множества.
Например,
1)Множество A={1,2,{3,4}}≠ содержит 3 элемента: 1 A, 2 A,{3,4} A, HO 3 4 A .
2)B={bn=b1∙qn-1; q 0 n=1,2,…} – бесконечное множество членов геометрической прогрессии со знаменателем q.
3)X={x: x2+x-2=0)} = {1,-2} – множество решений уравнения.
X={x: x2+1=0} = ≤
Известно, что для чисел определены отношения равенства «=» и сравнения – строгие «</>» и нестрогие «≤ / ≥» неравенства: 2<3 и 2 3 (2 не больше 3 или 3 не меньше 2) и
операции сложения «+», вычитания «-», умножения «х» и деления.
Пусть заданы множества A={a}, B={b}, С={c}. Определим для множеств:
1) отношения:
- равенство «=»: A=B A A : A B B B : B A - множества состоят из одинаковых |
|||||||||||||
- включения « »: А B A A : A B «А содержится в В (А является подмножеством В) |
|||||||||||||
Следствия |
|
|
|
|
|
|
|
|
|
|
. 2) Конечное множество с n |
||
. 1) |
Очевидно, что A {a}: A A A |
|
|
|
|||||||||
элементами имеет 2n подмножеств. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Например, множество A={1,2,{3,4} } имеет 23 =8 подмножеств: |
|||||||||||
2) операции: |
, A, {1}, {2},{{3,4)}, {1,2}, {1,{3,4}}, {2,{3,4}} A |
||||||||||||
|
|
|
хотя |
|
|
|
|
|
|
|
|
||
- объединение(“сумма”) множеств « »: |
|
С=A |
|
|
B C C : C A C B |
- состоит только из |
|||||||
тех элементов, которые принадлежат |
|
|
бы одному из множеств. |
||||||||||
|
|
||||||||||||
- пересечение(“произведение”) множеств « »: |
|
С=A |
|
B C C : C A C B |
- состоит |
||||||||
только из тех элементов, которые принадлежат |
обоим множествам. |
||||||||||||
|
|
|
|
|
|
||||||||
- разность множеств «\»: С=A \ B C C : C A C B - состоит только из тех
элементов A, которые не принадлежат В.
2
МНОЖЕСТВO A={a: F(a)} F(α) ==> α A; F((α) ) ==> α A
A={a}, B={b}, C={c} |
|
|
|
|
Включение “ : A |
B a A: a B |
b B: b A |
|
|
Объединение множеств “U : C=A |
B c C: c A |
c B |
||
Пересечение множеств “ |
: C=A |
B c C: c A |
c B |
|
Разность множеств |
\ : |
C=A \ B c C: c A |
c B |
|
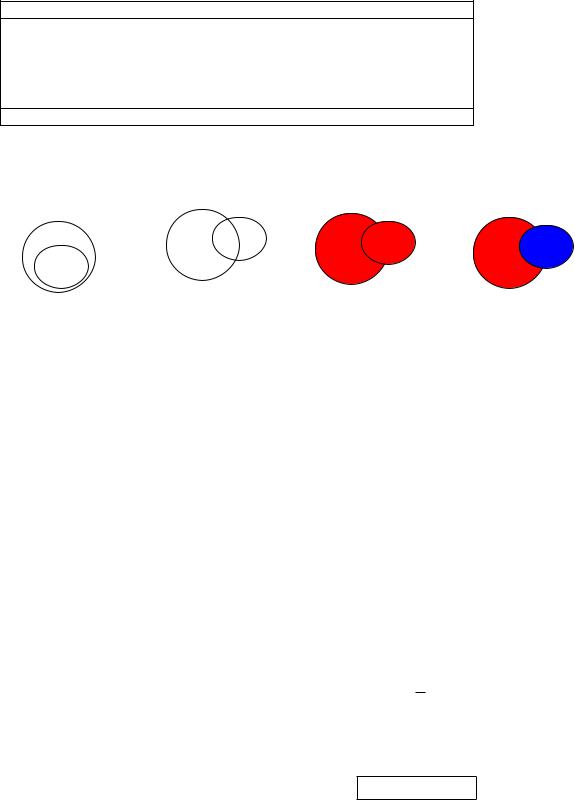
Иллюстрация «кругами Эйлера»: каждая точка круга – элемент множества.
|
A |
B |
A |
B |
|
B |
A |
C |
|
A |
|||
|
|
|
||||
B |
|
|
|
|
|
|
B A || |
C=A B |
|| |
C=A B |
|
|| |
C=A/B |
B B : B A |
|| C C : C A C B |
|| C C : C A C B || C C : C A C B |
||||
|
|
|
|
|
|
|
3) Множество A={a} называется замкнутым относительно операции (*), если результат операции для любых элементов множества принадлежит множеству
a, b A : (*)A A A(*)B A
Известно, что числовые множества:
|
|
|
|
|
|
|
|
|
|
N={1,2.3,…,n,n+1,…} |
– множество натуральных чисел замкнуто отн. “+” и “X”, HO не “-”.“ |
|
|||||||
|
|
||||||||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||
Z={0,±1, ±2,…., ±n, ±n+1,…} |
- множество целых чисел замкнуто отн. “+”,“x” и ”-“, HO не “ |
||||||||
|
|||||||||
|
|
|
|||||||
|
|
|
|
|
|
|
|||
Q ={ |
M |
: M Z } |
- множество рациональных чисел замкнуто отн. |
“+”, ”-“ , “x”, “ ” |
|
|
|||
|
|
|
|||||||
|
N |
N N |
|
|
|
|
|||
x Q : х- бесконечная периодическая десятичная дробь:. 2 0.666.. 0.(6) 0.667 (3 в.з.ц)
3
Иррациональные числа – числа, определяемые бесконечной непериодической десятичной дробью.
R = Q U {Ирр.} - множество вещественных чисел N Z Q R
Замечание. Во множестве вещественных (действительных) чисел R:
[1] определены:
|
|
|
|
|
|
|
|
a |
0 |
|
- модуль числа “|a|”: a R ! |
|
a |
|
0 : |
|
a |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
a |
0 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A,
;
A

|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- “арифметический корень натуральной степени N |
|
|
”. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
" Арифметическим корнем натуральной степени |
n N из |
неотрицательного числа a 0 |
||||||||||||||||||||||||||||||||||||
называетсянеотрицательное число N |
|
|
0 , степень " n" которого равна этому числу" |
|||||||||||||||||||||||||||||||||||
A |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
a 0 n N |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a 0 n N ! |
N |
A |
0 : ( |
N |
A ) |
n |
a |
N |
|
n |
a 0 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
A : 2. |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
n a a |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
m |
|
|
|
|
|
|
|
1 |
|
a 0 |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
a n N A ; a n (N A )m ; a n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
N A |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a x |
|
|
|
|
|
|
|
|
|
(a x ) y |
|
|
|
|
|
|
|
|
||||||
a x y a x a y ; a x y |
|
|
|
; a x y |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
y |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
(a y ) x |
|
|
|
|
|
|
|
|
||||
ЭКЗ-1 Записать определение |X+3| и найти решения уравнения |x+3|= 2x-5
ЭКЗ-2 Записать определение (х+3)1\2 и найти решения уравнения (х+3)1\2 = 2x-5 [2] Во множестве R квадратное уравнение ax2+bx+c=0 a 0 в зависимости от
дискриминанта D=b2-4∙a∙c имеет либо одно, либо два решения, либо решений не имеет.
|
|
D 0 |
|
b |
|
|
||
|
|
|
|
{ |
|
}; |
|
|
|
|
|
|
|
||||
|
|
|
|
|
2a |
|
|
|
|
|
|
b |
|
|
|||
a, b, c, x R a 0 : X {x : ax |
2 |
D 0 |
D |
|||||
|
bx c 0 a 0} |
|
{ |
2a |
}; |
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
D 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[3] В R не определены: деление на ноль и корень натуральной степени из отрицательного числа
[4] Вещественное число X R отображается точкой М(х) с координатой “x” на числовой прямой (ЧП): X R M(x).
[5] В R определены подмножества – “интервалы”:
[a,b] = {x: A≤X≤B} R – закрытый; (a,b) = {x: A<X<B} – открытый; [a,b), (a,b] – полуоткрытые
ЭКЗ-3 По «знаковой картинке f(x) на ЧП» записать множества≤ : X1= {X: F(X)=0 } =?; X2={X: F(X)>0}; X3= {X: F(X) 0}
-3 |
-2 |
|
-1 |
|
|
|
|
|
|
5 |
|
|
|
1 |
2 |
3 |
4 |
|
X |
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
