
Первый семестр / Лекции ФЭЛ вечерка МУС К.Ф. / ЛВП / Задачи на L и P
.pdf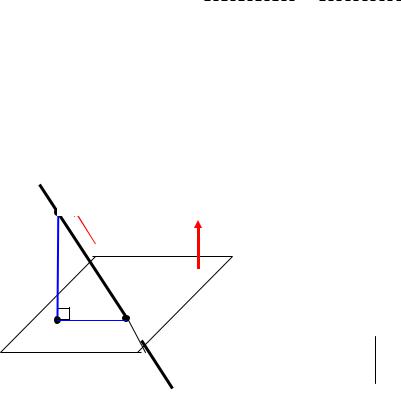
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 t |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
x 1 |
|
|
|
|||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
1 |
) |
|
2 |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
2 |
|
|
|
|||||||||
L1(A(1,2,3); SL1 |
y |
L2(B(1,0, 3); SL 2 |
|
2 |
|
|
|
y |
|
|
|
||||||||||||||||||||||||
|
|
|
2 |
|
|
3 2t |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
3 |
|
|
||||||
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
L1 |
s |
L2 |
|
|
|
|
||||||||||||
(1) |
Угол между прямыми: |
L1, L2 (s |
|
|
, s |
|
|
) |
ARCCOS |
|
|
|
|
|
|
|
ARCCOS( |
|
) 1000 |
||||||||||||||||
L1 |
L2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|| sL1 |
|| || sL2 |
|| |
|
|
6 |
|
|||||||||
(3) |
Точка пересечения двух прямых: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x 1 t 1 |
|
t |
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
tC 2 |
|
|
|
|||||||||
C L1 L2 |
|
|
|
|
|
1 1 |
|
|
0 |
|
|
|
|
1 0 |
|
|
|
! C( 1,4, 1) |
|||||||||||||||||
y 2 t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
2 |
||||||||||||
|
|
|
|
|
|
|
1 |
|
2 |
|
|
2 |
|
|
|
|
0 |
|
0 |
|
|
|
|
0 |
|
|
|
|
|
||||||
|
|
|
z 3 2t |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
2 1 |
|
6 |
|
|
|
0 |
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
======================================================================
Пусть |
в |
R3 |
заданы |
|
точки |
A(1;1;2); |
B(1;2;1);C(2;1;1);D(1;2;3) |
|
|
|
|
AB(0,1,-1); AC(1,0,-1); DA(0,1,1) |
|||
|
|
LN(D;SN=nP) |
|
|
|
|
|
L( A; SL ) |
|
S |
|
|
|
|
|
|
D |
L |
|
nP |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
P( A; nP ) |
|
|
А |
|
Е |
A L P; |
E LN P |
|
|
|
|
|
|
|
|
|
H || |
D |
E || |
ПРnP |
|
D |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[1] Плоскость/прямая через три/две заданные точки.
|
ABxAC} коорд. уравнение плоскости. |
A, B, C P P(M0 {A, B, C};nP |
A, B L L(M0 {A, B}; SL |
AB} параметрическое уравнение прямой. |
||||||
|
i |
j |
k |
|
1 |
|
|
|
|
|
|||||
nP = AB x AC=DET |
0 |
1 |
1 |
|
1 |
|
|
|
1 |
0 |
1 |
|
1 |
|
|
P(A; n =[1;1;1]t): 1(x-1)+1(y-1)+1(z-2)=0 x+y+z=4 |
|||||||
|
|
|
|
|
|
|
|
|
|
x 1 0t |
|
|
|
||
L(A; SL=AB=[0;1;-1]T): |
y 1 t |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
z 2 t |
|
|
|
||
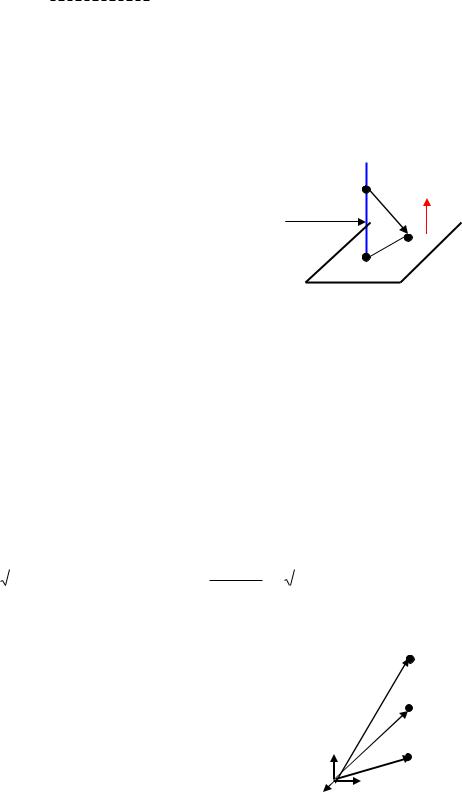
[2] Прямая L как линия пересечения двух плоскостей P1, P2.
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Ур е P1( x, y, z), |
|
||||||
L(M |
|
P2 |
1. |
M |
0 |
: |
|
е P2( x, y, z) |
|
||||||
0 ; sL ) P1 |
|
|
|
|
Ур |
|
|||||||||
|
|
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
s |
n |
2 |
s |
n |
1 |
x n |
2 |
||
|
|
|
|
|
|
|
L |
|
L |
|
|
||||
|
|
|
[1, 1,1]T } P2 : x z 2 |
n2 [1,0,1]T |
|||||||||||
P1(B(1,2,1), , n1 |
|||||||||||||||
x |
1 ( y 2) ( z 1) 0 |
|
|||||||
1. |
z 2 |
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
i |
j |
k |
|
|
|
|
|
1 |
|
|
|
|||
2. SL |
[n1 x n |
2] |
1 |
1 |
|||||
|
|
|
|
|
1 |
0 |
1 |
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
x z |
|
|||
0 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
|
0 |
|
M 0 ( 1,2,1) |
1 |
0 |
1 |
2 |
|
0 |
1 |
0 |
|
2 |
y 2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x |
y |
z |
|
|
|
|
|
|
|
|
z R |
|
||
|
1 |
|
|
|
|
|
x 1 t |
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
|
|
L( M 0 ; SL ) : y 2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
z 1 t; t R |
|
|||||
|
|
|
|
|
|
|
|
||||||||
[3]. Проекция E точки D(1,2,3) на плоскость P(A(1;1;2); nP=[1;1;1]t).
|
|
|
|
|
L(D,sL=nP) |
1. LN P D LN LN ( D; S N nP ) |
|
|
|||
D |
|||||
Алгоритм : |
E LN P |
|
|
|
nP |
|
H=|DE| |
||||
2. |
|
|
|
||
Р
А
Е
P(A(1,1,2); nP =[1;1;1]t) x+y+z=4; D(1;2;3)
|
x 1 t, |
|
t |
|
t, |
1. LN(D;SL=nP= [1,1,1] ) |
y 2 |
|
|
|
t |
|
z 3 |
|
|
P : x y z 4, |
6 3t 4, |
||
|
|
1 t, |
|
t, |
2. E LN P : |
L : x |
x 1 |
||
|
|
|
|
|
|
y 2 t, |
y 2 t, |
||
|
|
t |
|
t |
|
z 3 |
z 3 |
||
tE |
2 / 3, |
|
|
|
|
|
|
|
||
xE |
1 |
/ 3, |
E( |
1 |
|
4 |
|
7 |
|
|
|
4 / 3, |
|
, |
|
, |
|
) |
|||
3 |
3 |
3 |
||||||||
yE |
|
|
|
|
||||||
|
7 |
/ 3 |
|
|
|
|
|
|
|
|
zE |
|
|
|
|
|
|
|
|||
[4].Расстояние Н от заданной точки D до заданной плоскости P.
|
|
|
|
|
|
|
1 |
|
4 |
|
7 |
|
|
|
|
1. |
||||
E LN |
P E( |
|
|
, |
|
|
, |
|
|
) |
|
|||||||||
3 |
3 |
3 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
|||||||
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
4 |
|
2 |
|
|
2 |
3 |
|
|
2. |
|||||||
|
|
|
|
|
|
|||||||||||||||
H | D E( |
|
, |
|
, |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|||
3 |
3 |
3 |
|
|
3 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
A P |
|
|
|
|
|
|
|
|
|
|
|
||
D |
A(0,1,1); nP (1,1,1) |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
D A nP |
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
H | ПР |
D A | |
|
|
|
|
|
|
3 |
|||||
nP |
|
|
|
|
|| nP |
|| |
|
|
|
|
|
||
[5]. Точка C, симметричная заданной точке D относительно заданной плоскости P. |
|
D |
|||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rD |
|
|
|
|
|
T |
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
rE |
|
|
[1,4,7] ; |
rD |
[1,2,3] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E P |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
T |
|
1 |
|
2 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
rC |
rD 2D E |
rD |
2 rE |
rD |
2 rE |
rD |
|
|
[ 1;2;5] |
C( |
|
; |
|
; |
|
) |
|
|
|
||||
3 |
3 |
3 |
3 |
rE |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rC |
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
