Готовые билеты / Формула Бернулли билет 17

1. Формула Бернулли.

где Cnk — число сочетаний, q = 1 − p.

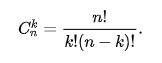
2. Дисперсия.

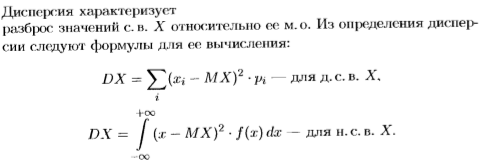
3. Плотность распределения многомерной с.в.

Плотность распределения многомерной с.в. – это такой закон распределения, выраженный функцией f(x,y), которая получена путем взятия смешанной второй (в зависимости от «меры») производной (по у и по х) от функции распределения F(x,y).

4. Доверительный интервал для параметра распределения Пуассона.

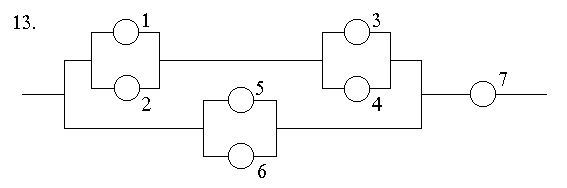
5. Вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи равны соответственно 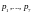. Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока.

X – вероятность успешной работы цепи

X = X1 * X2

X2 = p7

X1 = (p1+p2-p1*p2) * (p3+p4-p3*p4) + (p5+p6-p5*p6) - (p1+p2-p1*p2)*(p3+p4-p3*p4)*(p5+p6-p5*p6)

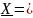1 - ((p1+p2-p1*p2) * (p3+p4-p3*p4) + (p5+p6-p5*p6) - (p1+p2-p1*p2)*(p3+p4-p3*p4)*(p5+p6-p5*p6)) * p7

6. Непрерывная случайная величина 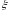задана своей плотностью распределения вероятностей:

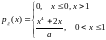
Найти значение постоянной a, функцию распределения, M и .

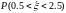Чтобы найти постоянную a, найдем фунцию распределения F:

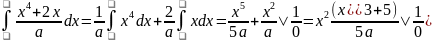
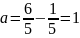
Таким образом, плотность распределения вероятностей:

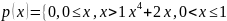
Функция распределения:

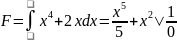
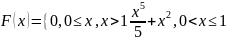
Находим мат ожидание:

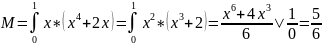
Ищем вероятность попадания в интервал:

P(0,5< <2,5) = F(x)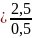 = F(x) 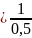+ F(x) 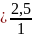= F(x) + 0 = =

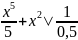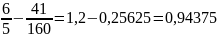
7. Случайная величина X распределена по нормальному закону с параметрами m=2, σ=3. Найти плотность распределения и математическое ожидание случайной величины .

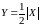Закон нормального распределения:

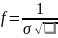
В нашем же случае:

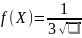
Функция монотонна (↑)

X = φ(y) = 2y

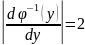
Теперь можем выразить плотность распределения с.в. Y через плотность распределения Х:

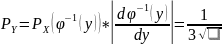
Теперь найдем математическое ожидание:

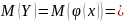2

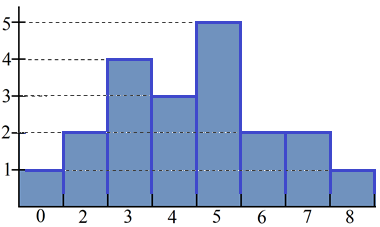
8. Дана выборка: 5 2 0 3 5 3 6 5 7 5 5 3 4 2 4 6 4 3 8 7.

Построить вариационный ряд, выполнить группировку данных, построить статистический ряд и эмпирическую функцию распределения, найти размах выборки, интервал варьирования, выборочную моду, выборочную медиану, выборочные верхнюю и нижнюю квартили, выборочное среднее, выборочную дисперсию и несмещенную дисперсию. Построить гистограмму.

Упорядоченный (Вариационный) ряд: 02233334445555566778

Статистический ряд:

xi	0	2	3	4	5	6	7	8
ni	1	2	4	3	5	2	2	1
pi*	0,05	0,1	0,2	0,15	0,25	0,1	0,1	0,05

Эмпирическая функция распределения:

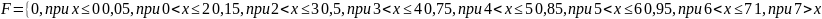
Размах выборки:

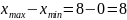
Интервал варьирования:

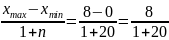
Выборочная мода: 5

Выборочная медиана:

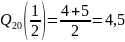
Выборочный верхний квартиль:

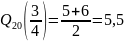
Выборочный нижний квартиль:

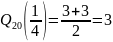
xi	0	2	3	4	5	6	7	8
ni	1	2	4	3	5	2	2	1
pi*	0,05	0,1	0,2	0,15	0,25	0,1	0,1	0,05

Выборочное среднее:

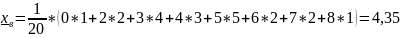
Выборочная дисперсия:

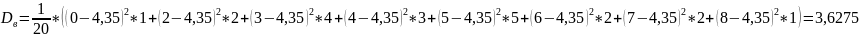
Несмещенная дисперсия:

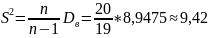
Гистограмма: