ЛАБА31
.docxФедеральное агентство связи
Ордена трудового красного знамени федеральное государственное
бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра «Теория электрических цепей»
Лабораторная работа №31
«Исследование входных частотных характеристик в RL-цепи»
Выполнила: студентка группы БСТ2001
Курило А.А.
Проверил: доц. кафедры ТЭЦ
Микиртичан А. Г.
1 Цель работы
С помощью программы Micro-Cap исследовать входные амплитудно-частотные (АЧХ) и фазочастотные (ФЧХ) характеристики RL-цепи. Сравнить АЧХ и ФЧХ, полученные с помощью программы Micro-Cap, с аналогичными характеристиками, полученными расчётным путём.
2 Задание для лабораторной работы
Изучить основные положения ТЭЦ о частотных характеристиках электрических цепей. Выполнить предварительный расчет, письменно ответить на вопросы для самопроверки.
3 Предварительный расчет
3.1 Формулы
Z(BX) = U(BX)/I = Z(ω)e^(jφ(z)*(ω))=Z(2πf) e^(jφ(z)*(2πf) ), где
U(BX) – комплексное входное напряжение;
I = U(BX)/Z(BX) – комплексный входной ток;
U(R) = R*I – комплексное напряжение на резисторе;
j = √-1 – мнимая единица;
ω = 2πf – угловая частота;
f – частота;
U(L) = jωL*I – комплексное напряжение на катушке;
|Z(BX) | = Z(2πf) – модуль комплексного входного сопротивления (АЧХ);
arg(Z(BX)) = φ(z)*(2πf) – аргумент (фаза) комплексного входного сопротивления (ФЧХ).
Z(BX) = Re(Z(BX))+jIm(Z(BX)) = R1+jX(L) = √(R1^2+X(L)^2)*
*e^(-jarctg(X(L)/R1)) = R1 √(1+(f/f(гр))^2)*e^(-jarctg(f/f(гр)));
Re(Z(BX)) = R1 – резистивное входное сопротивление,
Im(Z(BX)) = X(L) – реактивное входное сопротивление,
X(L) = ωL – индуктивное сопротивление катушки L1
F(гр) = R1/(2πL1) – Граничная частота RL-цепи.
3.3 Результаты предварительно расчета
Таблица 1 – Результаты полученные путем предварительного расчета
f, кГц |
f/fгр |
|
|
|
I,A |
|
|
2 |
5,65 |
565,49 |
574,26 |
79,9 |
0,00174 |
174,1 |
984,72 |
4 |
11,3 |
1130.9 |
1135.4 |
84,9 |
0,00088 |
88.07 |
996,11 |
6 |
17,0 |
1696,5 |
1699,4 |
86,6 |
0,00059 |
58,84 |
998,27 |
8 |
22,6 |
2261,9 |
2264.2 |
87,5 |
0,00044 |
44,17 |
999,02 |
10 |
28,3 |
2827,4 |
2829,2 |
87,9 |
0,00035 |
35,35 |
999,38 |
12 |
33,9 |
3392,9 |
3394.4 |
88,3 |
0,00029 |
29,46 |
999,57 |
14 |
39,6 |
3958.4 |
3959,7 |
88,6 |
0,00025 |
25,25 |
999,68 |
4 Компьютерные расчеты
4.2 Схема
Собрать схему с источником синусоидального напряжения, резистором и катушкой.
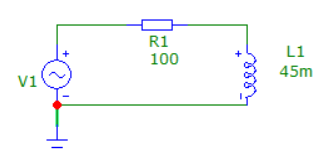 Рисунок
1 – Cхемa RL‐цепи.
Рисунок
1 – Cхемa RL‐цепи.
4.2 Исследование частотных характеристик RL‐цепи
На рисунке 2 изображен график зависимости модуля входного сопротивления от частоты
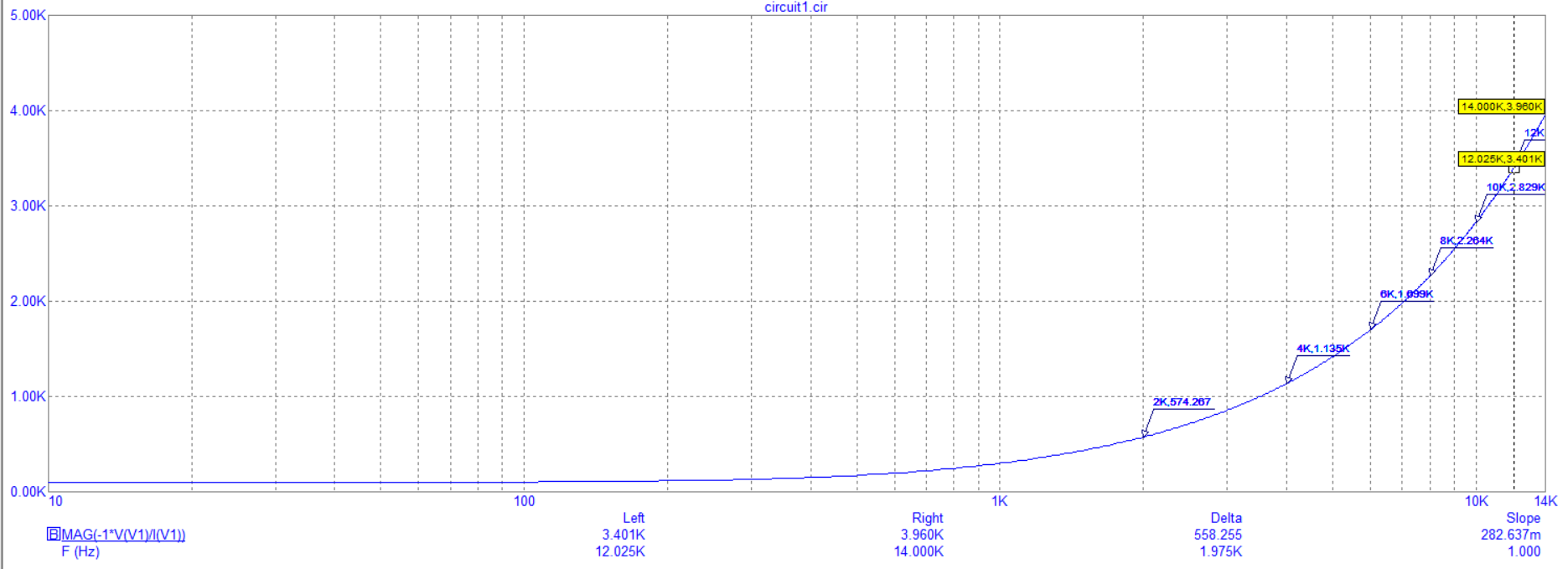 Рисунок
2 – График зависимости модуля входного
сопротивления от частоты
Рисунок
2 – График зависимости модуля входного
сопротивления от частоты
На рисунке 3 изображен график зависимости фазы входного сопротивления от частоты
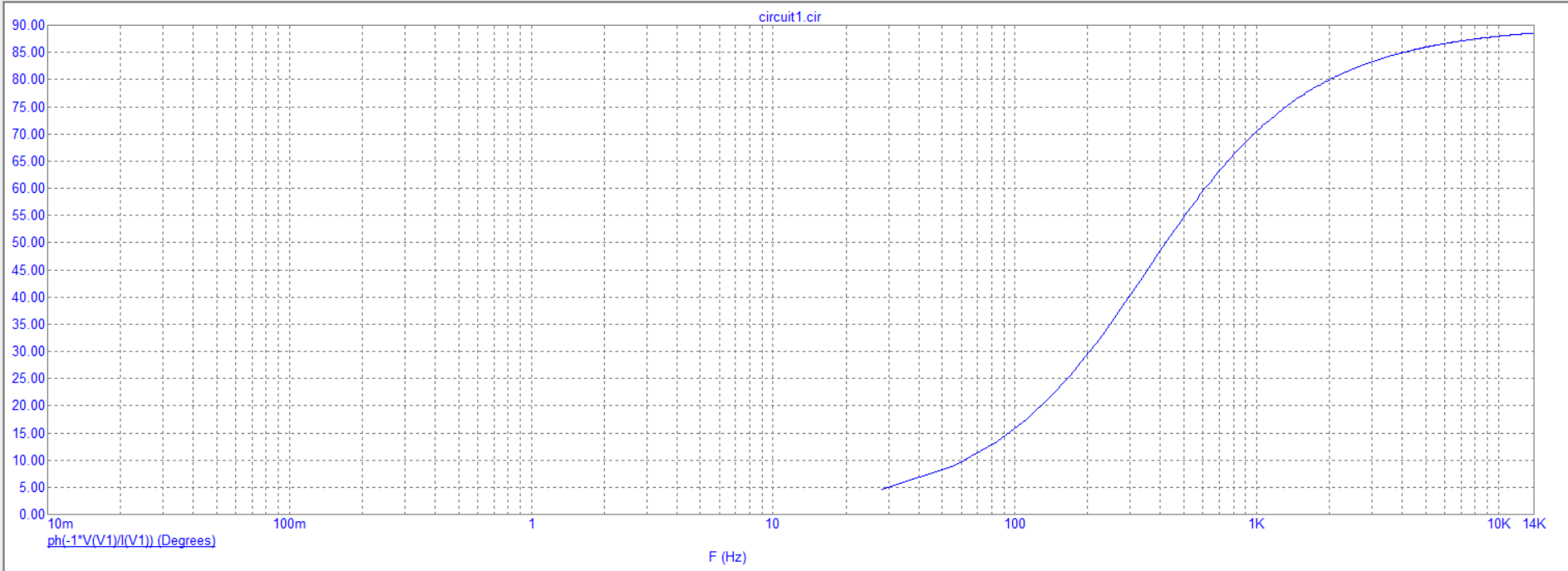 Рисунок
3 – График зависимости фазы входного
сопротивления от частоты
Рисунок
3 – График зависимости фазы входного
сопротивления от частоты
На рисунке 4 показан график зависимости модуля тока от частоты.
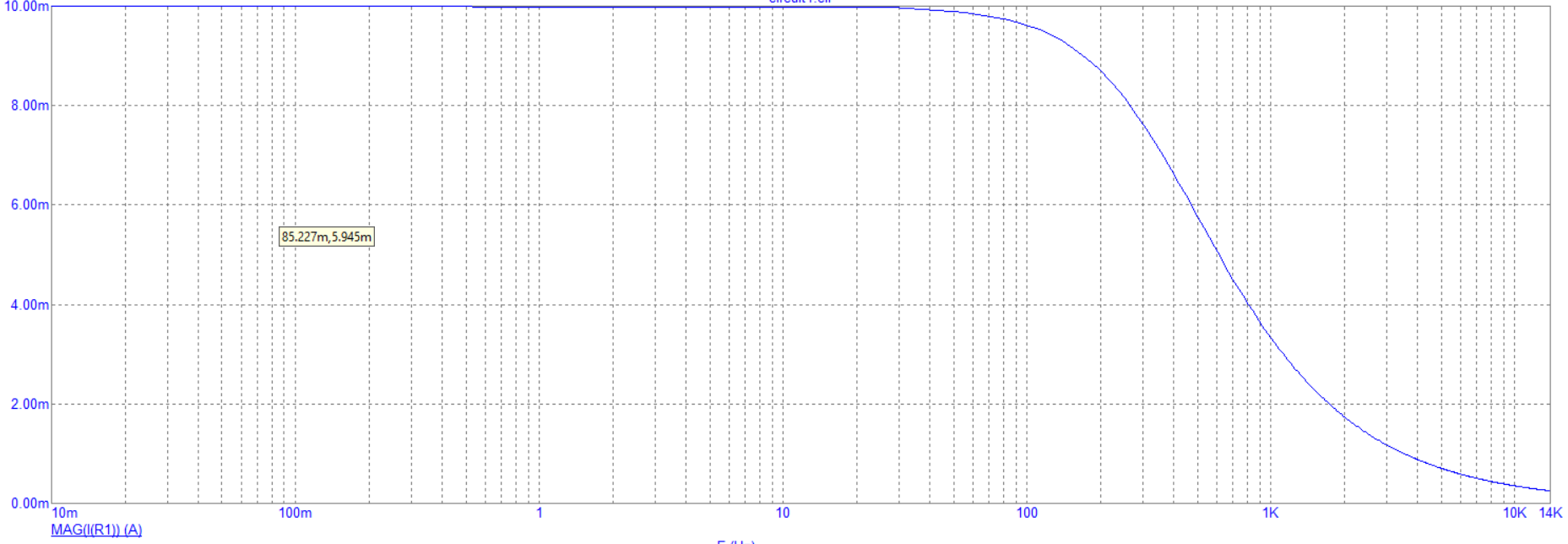 Рисунок
4 – График зависимости модуля тока от
частоты
Рисунок
4 – График зависимости модуля тока от
частоты
На рисунке 5 изображен график зависимости модуля напряжения на резисторе от частоты.
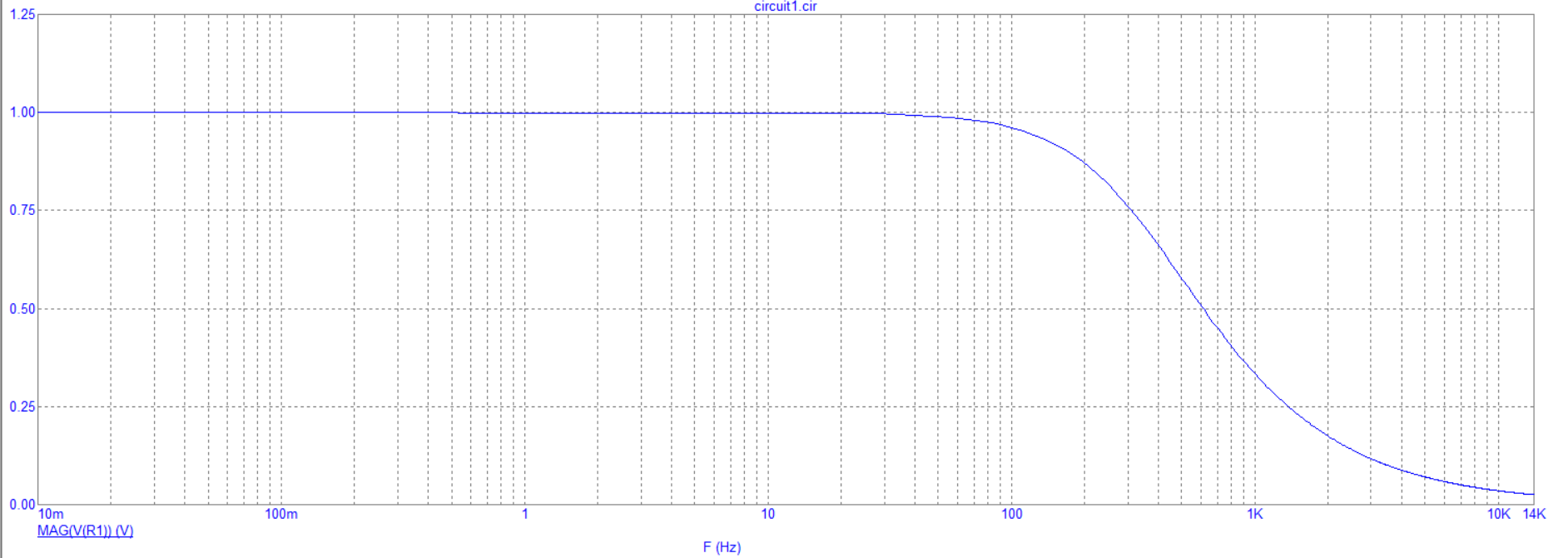 Рисунок
5 - График зависимости модуля напряжения
на резисторе от частоты
Рисунок
5 - График зависимости модуля напряжения
на резисторе от частоты
На рисунке 6 изображен график зависимости резистивного сопротивления от частоты.
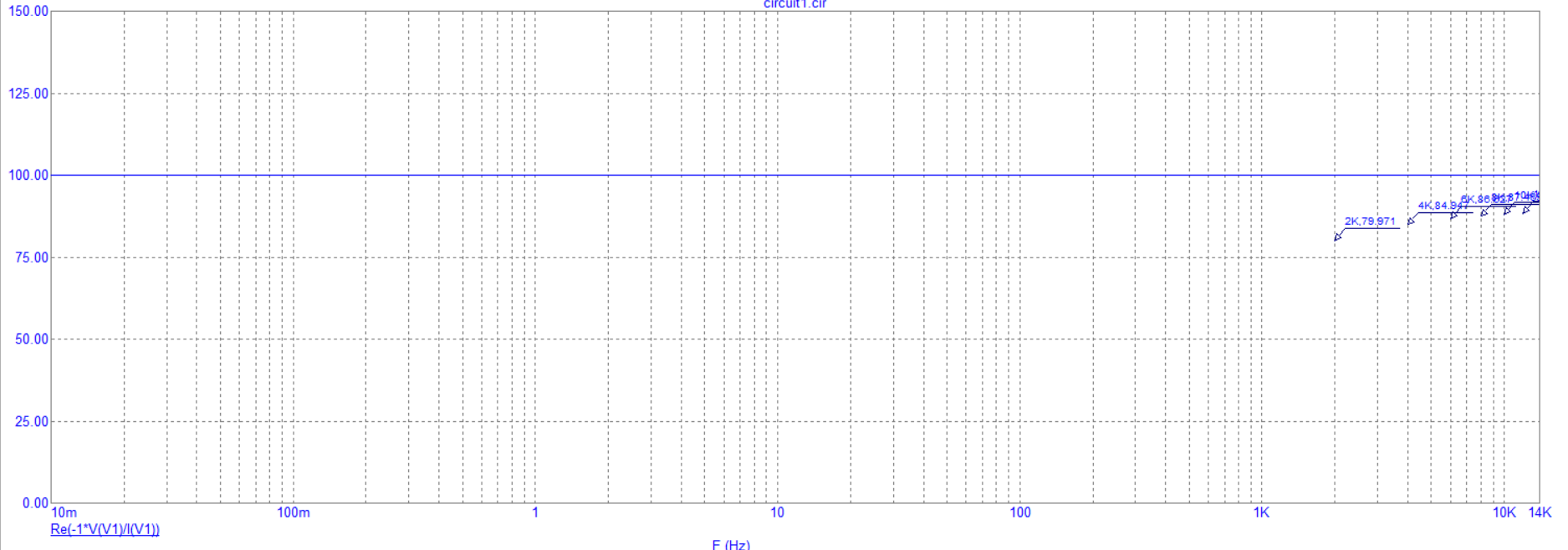 Рисунок
6 - График зависимости резистивного
сопротивления от частоты
Рисунок
6 - График зависимости резистивного
сопротивления от частоты
На рисунке 7 показан график зависимости индуктивного сопротивления от частоты.
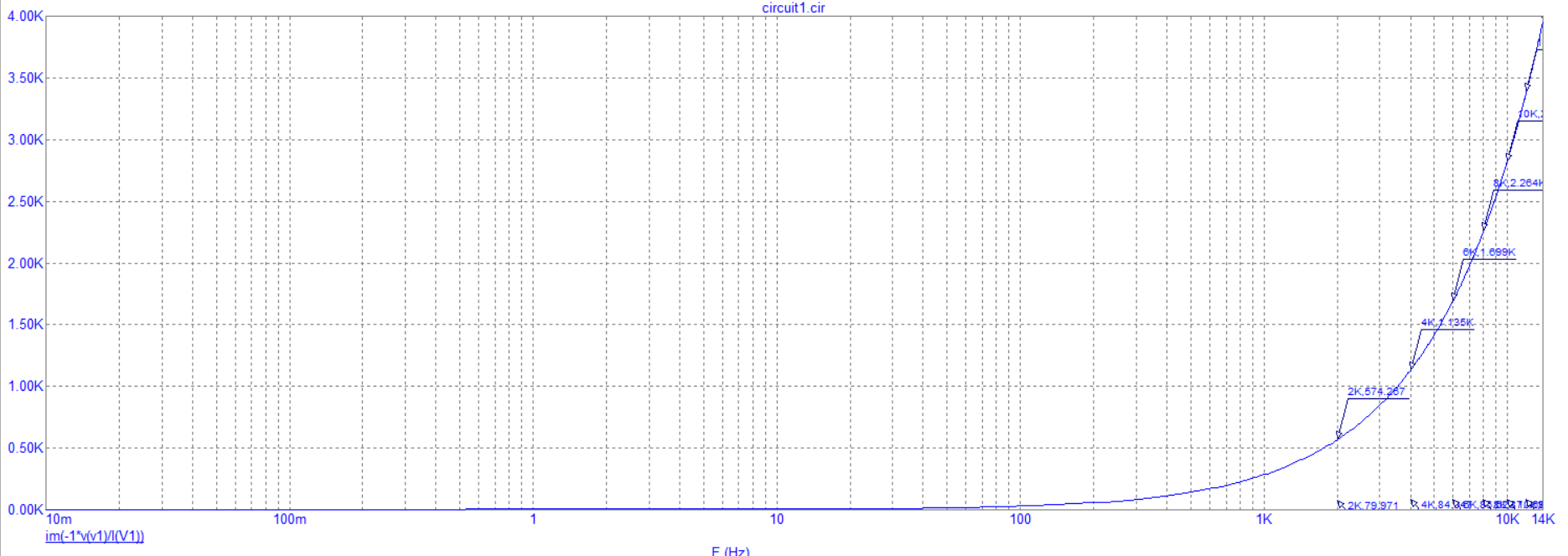 Рисунок
7 - График зависимости индуктивного
сопротивления от частоты
Рисунок
7 - График зависимости индуктивного
сопротивления от частоты
На рисунке 8 показан график зависимости модуля напряжения на катушке от частоты.
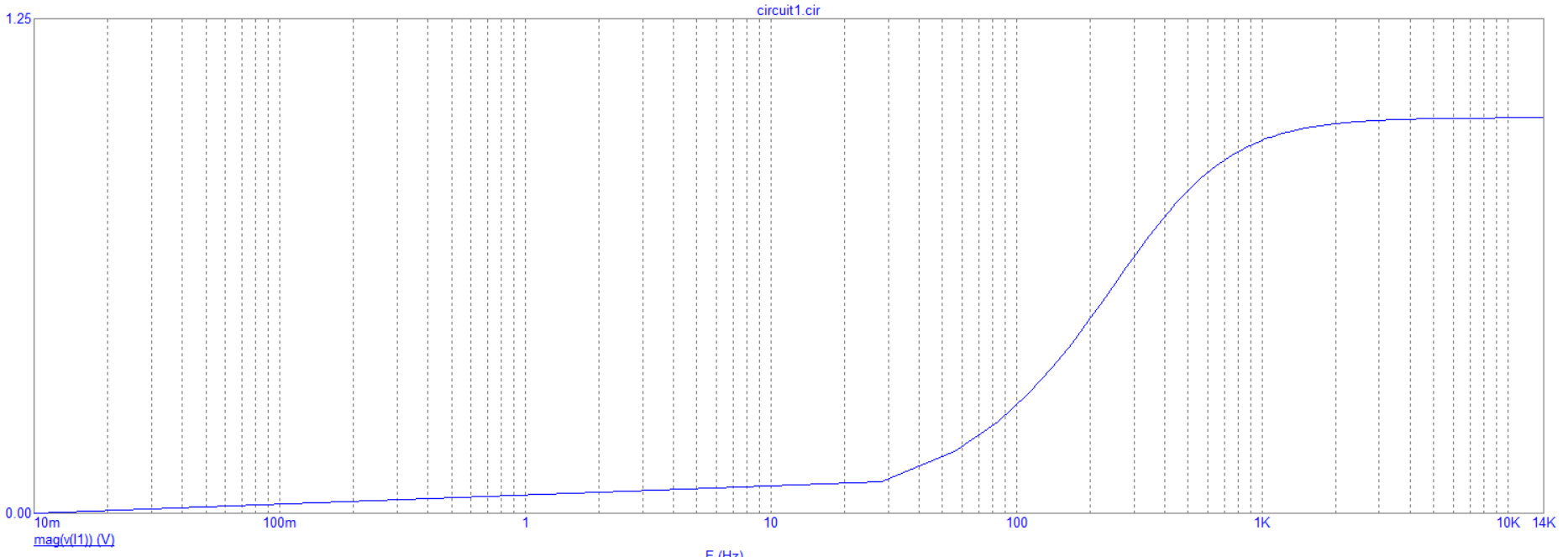 Рисунок
8 - График зависимости модуля напряжения
на катушке от частоты
Рисунок
8 - График зависимости модуля напряжения
на катушке от частоты
4.3 Результаты компьютерных расчетов
Таблица 1 – Результаты компьютерных расчетов
f, кГц |
f/fгр |
|
|
,град. |
I,A |
|
|
2 |
5,65 |
565,4 |
574,2 |
79,9 |
0,00174 |
174,1 |
984,72 |
4 |
11,3 |
1130 |
1135 |
84,9 |
0,00088 |
89 |
996,11 |
6 |
16,9 |
1696,4 |
1699,6 |
86,6 |
0,00058 |
58,8 |
998,27 |
8 |
22,6 |
2261,9 |
2264 |
87,4 |
0,00044 |
44,1 |
999,02 |
10 |
28,2 |
2827,4 |
2829,3 |
87,9 |
0,00035 |
35,3 |
999,37 |
12 |
33,9 |
3392,9 |
3394 |
88,3 |
0,00029 |
29,4 |
999,56 |
14 |
39,5 |
3956 |
3960,1 |
88,5 |
0,00025 |
25,2 |
999,69 |
Вопросы для самопроверки
1) Какая частота называется граничной для RL – цепи?
Ответ. Граничная частота RL – цепи – частота, на которой действительная и мнимая часть комплексного входного сопротивления равны.
2)Каково значение модуля входного сопротивления RL – цепи на граничной частоте?
Решение.
На граничной частоте:
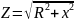
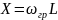
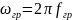
Ответ. |Zвх|=R√2 = 4241,28 Ом
3)Каково значение аргумента входного сопротивления RL - цепи на граничной частоте?
Решение.
На граничной частоте:
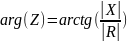
arg|Zвх|= |φвх|
Ответ. arg|Zвх|= 44,98°
4)К чему стремится модуль тока RL – цепи при увеличении частоты?
Решение.
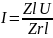
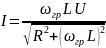

Ответ. С ростом
частоты входное напряжение цепи
возрастает, а модуль тока уменьшается,
следовательно
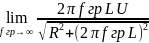 =
U
=
U
5) Чему равен модуль входного сопротивления RL – цепи при частоте, равной нулю?
Решение.
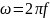
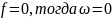
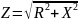
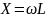
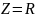
Ответ. Z = 3000 Ом
Москва 2021

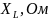
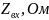
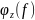 ,град.
,град.