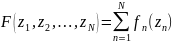- •(37) Графический метод решения задачи лп. (Гребенникова стр 120-122)
- •(39) Динамическое программирование. Постановка задачи. Принцип оптимальности.
- •(42) Постановка задачи оптимизации высот подвеса антенн ррл.
- •(43) Алгоритм динамического программирования при решении задачи оптимизации высот подвеса антенн ррл
где
 –
матрица Гессе (вторых производных). Если
матрица Гессе целевой функции вычисленная
в точке
–
матрица Гессе (вторых производных). Если
матрица Гессе целевой функции вычисленная
в точке
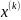 ,
является положительно определённой,
то точка
минимума функции
,
является положительно определённой,
то точка
минимума функции
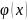 единственна и может быть найдена из
условия, что её градиент равен нулевому
вектору:
единственна и может быть найдена из
условия, что её градиент равен нулевому
вектору:
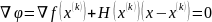 ,
следовательно,
,
следовательно,
 .
Алгоритм оптимизации, в котором
направление поиска определяется из
этого соотношения, называется методом
Ньютона, а направление
.
Алгоритм оптимизации, в котором
направление поиска определяется из
этого соотношения, называется методом
Ньютона, а направление
 – ньютоновским направлением, составляет
с вектором градиента тупой угол.
– ньютоновским направлением, составляет
с вектором градиента тупой угол.
(35) Метод многомерной оптимизации Гаусса-Зейделя.
Ответ представлен в пункте 32.
(36) Общая постановка задачи линейного программирования. Канонический вид.
Линейное программирование – математическая дисциплина, посвящённая теории и методам решения задач об экстремумах линейных функций на множествах, задаваемых системами линейных неравенств и равенств.
Основной задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции
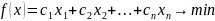
при выполнении условий (ограничений)
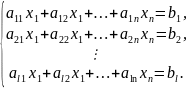
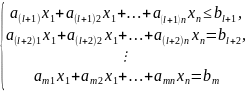
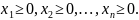
где
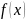 – линейная функция, a,
с – известные постоянные величины, х -
неизвестные величины, подлежащие
оптимизации, b
– значения соответствующих ограничений,
определяющие область допустимых
значений,
l
–
ограничения в виде равенств, (m
– l)
– ограничения в виде неравенств, n
– число неизвестных переменных.
– линейная функция, a,
с – известные постоянные величины, х -
неизвестные величины, подлежащие
оптимизации, b
– значения соответствующих ограничений,
определяющие область допустимых
значений,
l
–
ограничения в виде равенств, (m
– l)
– ограничения в виде неравенств, n
– число неизвестных переменных.
Данные ситуации имеют место быть:
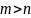
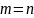
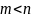
Если в исходной постановке задача максимизации, то необходимо домножить на (-1).
Если
в условии задачи линейного программирования
не содержатся ограничения-неравенства
то есть в
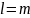 ,
то она называется задачей линейного
программирования в каноническом виде.
,
то она называется задачей линейного
программирования в каноническом виде.
Всегда задачу линейного программирования можно привести к каноническому виду:
Для этого в ограничения в виде неравенств нужно ввести дополнительные переменные
(37) Графический метод решения задачи лп. (Гребенникова стр 120-122)
Если задача линейного программирования содержит только две переменные и в ее условии нет ограничений-равенств, то такую задачу можно исследовать и решить графически.
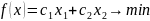
При ограничениях
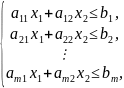
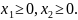
На
плоскости (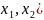 любое
из данных неравенств определяет
полуплоскость, лежащую по одну из сторон
от прямой
любое
из данных неравенств определяет
полуплоскость, лежащую по одну из сторон
от прямой
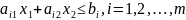 .
Для того чтобы определить расположение
этой полуплоскости относительно
граничной прямой, можно подставить
координаты какой-либо точки (при
.
Для того чтобы определить расположение
этой полуплоскости относительно
граничной прямой, можно подставить
координаты какой-либо точки (при
 проще всего взято начало координат) в
соответствующее неравенство и проверить
его выполнение.
проще всего взято начало координат) в
соответствующее неравенство и проверить
его выполнение.
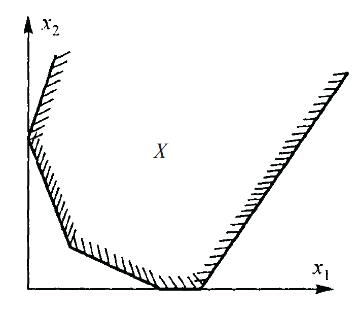 Таким
образом, допустимое множество X задачи
является пересечением первого квадранта
Таким
образом, допустимое множество X задачи
является пересечением первого квадранта
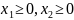 и полуплоскостей, соответствующих
неравенствам. Поэтому множество X
представляет собой либо:
и полуплоскостей, соответствующих
неравенствам. Поэтому множество X
представляет собой либо:
1) пустое множество, тогда задача не имеет решений
2) многоугольник
3) неограниченное многоугольное множество
В
случае пустого множества рассмотрим
семейство линий уровня функции
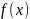
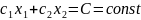
Которые
являются параллельными прямыми.
Антиградиент
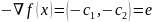 перпендикулярен прямым и указывает
направление убывания функции
.
Если перемещать параллельно самой себе
произвольную прямую, проходящую через
допустимое множество
перпендикулярен прямым и указывает
направление убывания функции
.
Если перемещать параллельно самой себе
произвольную прямую, проходящую через
допустимое множество
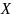 , в направлении e убывания функции
до тех пор, пока эта прямая будет иметь
хотя бы одну общую точку с множеством
X
, то в своем крайнем положении указанная
прямая пройдет через точку множества
,
в которой целевая функция f
(x)
принимает минимальное значение.
, в направлении e убывания функции
до тех пор, пока эта прямая будет иметь
хотя бы одну общую точку с множеством
X
, то в своем крайнем положении указанная
прямая пройдет через точку множества
,
в которой целевая функция f
(x)
принимает минимальное значение.
(38) Симплекс-метод решения задачи ЛП. (Гребенникова стр 131-135)
Рассматривается задача линейного программирования в каноническом виде при ограничениях, определяющих допустимое множество Х:
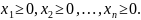
Пускай
ранг матрицы
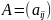 системы ограничений равенств задачи
линейного программирования в каноническом
виде равен рангу расширенной матрицы
системы ограничений равенств задачи
линейного программирования в каноническом
виде равен рангу расширенной матрицы
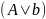 этой системы. Иначе система несовместна
(система линейных уравнений называется
совместной, если она имеет по крайней
мере одно частное решение (т. е. ее общее
решение не пусто)) и не имеет решений.
этой системы. Иначе система несовместна
(система линейных уравнений называется
совместной, если она имеет по крайней
мере одно частное решение (т. е. ее общее
решение не пусто)) и не имеет решений.
Выберем произвольный базисный минор матрицы A, порядка r. Этот минор соответствует первым r столбцам и строкам матрицы А.
Разрешим
систему относительно базисных переменных
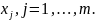 Для этого с помощью эквивалентных
преобразований приведем систему к виду:
Для этого с помощью эквивалентных
преобразований приведем систему к виду:
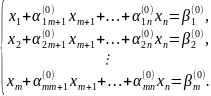
Отсюда решение системы запишем в виде
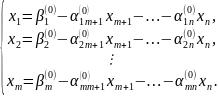
Положим
значения свободных переменных
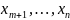 равными нулю:
равными нулю:
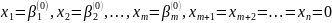
Или
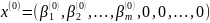
Получили базисное решение системы.
(39) Динамическое программирование. Постановка задачи. Принцип оптимальности.
Динамическое программирование — это подход к решению задач, который основывается на том, что исходная задача разбивается на более мелкие подзадачи, которые проще решить.
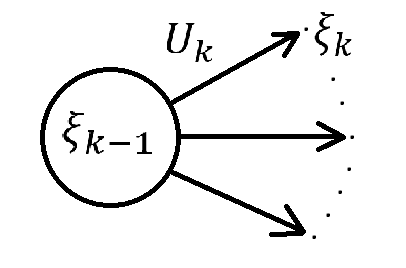
Пусть имеется объект, способный развиваться во времени, переходя от одного состояния к другому. Такой объект в задачах динамического программирования называется динамической системой. Множество всех состояний, которые может принимать эта система, развиваясь во времени, называется пространством состояний или фазовым пространством или множеством траекторий системы.
 Если
система состояний динамической системы
происходит в дискретные моменты времени,
то такая система называется динамической
системой с дискретным временем.
Именно такие системы и рассматриваются
в динамическом программировании.
Если
система состояний динамической системы
происходит в дискретные моменты времени,
то такая система называется динамической
системой с дискретным временем.
Именно такие системы и рассматриваются
в динамическом программировании.
Моменты
времени,
в которые происходит смена состояний
динамической системы будем обозначать
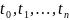 .
.
Предположим, что развитие во времени динамической системы происходит следующим образом:
В
начальный момент времени
 система находится в состоянии
система находится в состоянии
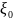 .
Переход из момента времени
.
Переход из момента времени
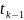 из состояния
из состояния
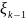 в состояние
в состояние
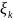 в момент времени
в момент времени
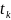 осуществляется за счёт некоторого
выбранного управления,
которое будем обозначать как
осуществляется за счёт некоторого
выбранного управления,
которое будем обозначать как
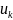 .
То есть, если система находится в
состоянии
,
то она может перейти в различные состояния
при разных управляющих воздействиях
.
То есть, если система находится в
состоянии
,
то она может перейти в различные состояния
при разных управляющих воздействиях
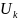 .
.
К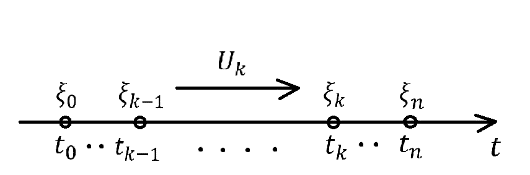 онкретное
значение состояния
зависит от предыдущего состояния и от
выбранного на данном шаге управления.
онкретное
значение состояния
зависит от предыдущего состояния и от
выбранного на данном шаге управления.
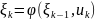
Предполагается, что на каждом шаге имеется свой набор различных управлений
После некоторого количества n-шагов развитие системы прекращается/система выключается
Набор
состояний от
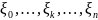 ,
через которые проходит динамическая
система, называется траекторией/фазовой
траекторией/траекторией движения.
В зависимости от количества уравнений
на каждом шаге возможно движение по
различным траекториям. В некоторых
случаях количество траекторий стремится
к бесконечности.
,
через которые проходит динамическая
система, называется траекторией/фазовой
траекторией/траекторией движения.
В зависимости от количества уравнений
на каждом шаге возможно движение по
различным траекториям. В некоторых
случаях количество траекторий стремится
к бесконечности.
Динамические системы, развивающиеся таким образом называются управляемыми.
При рассмотрении управляемых динамических систем (УДС) принято считать, что начальное состояние у всех возможных траекторий одинаковое.
Пусть
имеется УДС. Выбор той или иной траектории
определяется некоторым показателем
качества S,
зависящим от управлений на каждом шаге
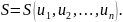
Физический смысл: доход (стоит задача максимизации -> max)
затраты (стоит задача их минимизации -> min).
При
решении задач ДП предполагается
выполнение условия: суммарный доход
равен сумме доходов на каждом шаге
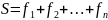 ,
где
,
где
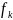 – доход на k-ом
шаге
– доход на k-ом
шаге
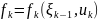 при изменении системы от
при изменении системы от
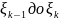 .
Тогда доход зависит от состояния, в
котором была система в начале и от
выбранного на данном шаге управления
.
Тогда доход зависит от состояния, в
котором была система в начале и от
выбранного на данном шаге управления
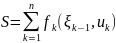
Такое представление показателя качества называется аддитивной целевой функцией ДП.
Задача ДП ставится следующим образом:
1) Имеется управляемая динамическая система, что означает:
1.1) выделено конечное число шагов n;
1.2) на каждом шаге указаны все возможные состояния , через которые может пройти динамическая система, фиксировано;
1.3) на каждом шаге заданы возможные управления, при чём указана функция, позволяющая по предыдущим состоянию и управлению определить в зависимости от управления в каком состоянии окажется система.
2)
Указана аддитивно-целевая функция на
каждом шаге. Решить задачу динамического
программирования означает найти набор
управлений
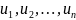 таким образом, чтобы оптимизировать
аддитивно-целевую функцию
.
таким образом, чтобы оптимизировать
аддитивно-целевую функцию
.
Каждой траектории динамической системы отвечает определенное значение целевой функции. Траектория, которой отвечает максимальное (минимальное) значение целевой функции, называется оптимальной траекторией.
Основная задача ДП найти оптимальную траекторию. Это называется альтернативной задачей ДП. Иногда ставится не одна альтернативная задача, а много.
Когда ставится выбор не одной оптимальной, а нескольких близких к оптимальной траектории, из этих нескольких отобранных траекторий наилучшая выбирается либо другими методами оптимизации, либо методом экспертных оценок.
Пусть к началу k-ого шага ДС находится в состоянии . Оставшийся путь система может пройти по различным траекториям, в зависимости от выбранного управления.
Каждой
траектории будет соответствовать свой
доход на участке от k-1
до n-ого
шага. Обозначим этот доход как
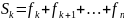 .
.
Обозначим
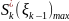 суммарный доход, начиная с первого до
последнего. Назовём его условным
максимальным доходом.
Условным, потому что зависит от
.
суммарный доход, начиная с первого до
последнего. Назовём его условным
максимальным доходом.
Условным, потому что зависит от
.
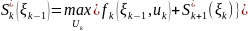
где максимум берётся по всем возможным управлениям на k-м шаге,
определяется выбранным на каждом шаге управлением .
Из выражения доказан принцип оптимальности ДП или принцип оптимальности Белмана. Теорема звучит так: при построении оптимальной траектории нужно выбирать управление на каждом шаге так, чтобы доход на этом шаге плюс максимальный доход на последующих шагах был наибольшим.
(40) Алгоритм решения задачи ДП. (Романовская 11 стр)
Исходя из принципа оптимальности Белмана можем сформулировать алгоритм оптимизации программы ДП в общем виде:
1 этап. (Движение от конца к началу). Начиная с конца последовательно находим условное оптимальное уравнение для всех возможных наборов условно оптимальных уравнений, условно оптимальных доходов и затрат.
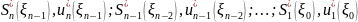
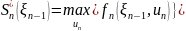
2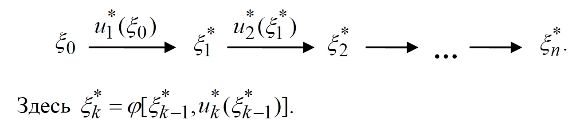 этап. (движение от начала к концу).
Двигаясь от начала, существенно используя
закрепленность начального состояния,
строим безусловную оптимальную
траекторию.
этап. (движение от начала к концу).
Двигаясь от начала, существенно используя
закрепленность начального состояния,
строим безусловную оптимальную
траекторию.
Ограничения:
- заранее знать все возможные состояния
- целевая функция аддитивная
(41) Общая характеристика задач оптимизации РРЛ.
Наиболее важными частными задачами оптимизации построения радиорелейных линий, а также местных и технологических сетей фиксированной радиосвязи являются следующие:
оптимизация выбора мест расположения радиорелейных станций на трассах РРЛ с линейной топологией;
оптимизация трасс местных и технологических РРЛ с кольцевой топологией;
оптимизация высот подвеса антенн на многоинтервальной РРЛ;
оптимизация мощностей передатчиков на интервалах РРЛ с линейной топологией и двухчастотными планами распределения частот радиоканалов;
оптимизация характеристик ответвлений от существующих РРЛ при повторном использовании частот;
оптимизация мощностей передатчиков на интервалах местных и технологических сетей радиосвязи со звездообразной топологией.
Обобщённая математическая модель задачи оптимизации цифровой системы радиосвязи имеет вид:
Найти
такое решение
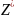 ,
для которого целевая функция
,
для которого целевая функция
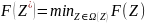
При условиях
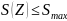
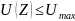
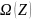 – множество
возможных вариантов решения;
– множество
возможных вариантов решения;
 – значение
целевой функции, соответствующее Z;
– значение
целевой функции, соответствующее Z;
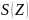 – значение
показателя качества по ошибкам,
соответствующее Z;
– значение
показателя качества по ошибкам,
соответствующее Z;
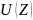 – значение
показателя неготовности, соответствующее
Z;
– значение
показателя неготовности, соответствующее
Z;
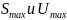 –
соответственно
максимально допустимые значения
показателей качества по ошибкам и
неготовности, определяемые в соответствии
с рекомендациями Международного союза
электросвязи.
–
соответственно
максимально допустимые значения
показателей качества по ошибкам и
неготовности, определяемые в соответствии
с рекомендациями Международного союза
электросвязи.
Каждый
из возможных вариантов построения
системы радиосвязи представляет собой
упорядоченную последовательность
элементов
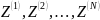 ,
характеризующих возможные способы
построения соответствующих подсистем,
входящих в состав рассматриваемой
системы:
,
характеризующих возможные способы
построения соответствующих подсистем,
входящих в состав рассматриваемой
системы:
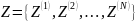
N – общее число звеньев системы
При
этом
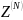 представляет собой такую же упорядоченную
последовательность элементов и
принадлежит к множеству возможных
вариантов построения n-го
звена.
представляет собой такую же упорядоченную
последовательность элементов и
принадлежит к множеству возможных
вариантов построения n-го
звена.
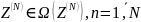
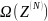 – множество
возможных вариантов построения n-го
звена
– множество
возможных вариантов построения n-го
звена
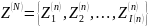
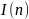 – число
параметров n-го
звена, измеряемых в процессе оптимизации
системы радиосвязи (измеряемых параметров)
– число
параметров n-го
звена, измеряемых в процессе оптимизации
системы радиосвязи (измеряемых параметров)
При
этом
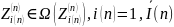 ,
где
,
где
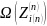 - множество возможных вариантов
- множество возможных вариантов
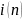 -го
измеряемого параметра n-го
звена.
-го
измеряемого параметра n-го
звена.
В случае многовариантной оптимизации нужно найти k – решений Z:
найти
такие
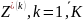 ,
для которых
,
для которых
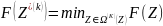
При условиях:
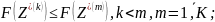
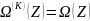
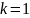
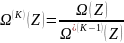
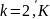
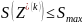
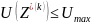
В общем виде сепарабельная функция может быть записана в виде:
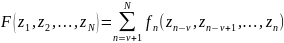
*Сепарабельность функции — в случае функции нескольких переменных (аргументов) возможность разделения влияния аргументов на общий результат.
Где
 – измеряемые параметры
– измеряемые параметры
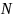 – число
измеряемых параметров
– число
измеряемых параметров
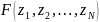 – сепарабельная
функция N
измеряемых параметров
– сепарабельная
функция N
измеряемых параметров
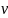 – степень
уменьшения сепарабельности,
– степень
уменьшения сепарабельности,
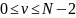
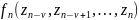 – функция
произвольного вида, зависящая от (
– функция
произвольного вида, зависящая от (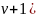 измеряемых параметров.
измеряемых параметров.
В
случае
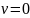 функция считается полностью сепарабельной
функция считается полностью сепарабельной