От характеристической функции большей мерности можно получить характеристическую функцию меньшей размерности, приравняв лишние аргументы нулю

Числовые характеристики: (Тихонов Харисов стр 34)

- совместные начальные моменты определяются как мат ожидания соответствующих произведений

Момент , относящийся к n различным случайным величинам , называется n-мерным начальным моментом -го порядка.

Совместные моменты можно определить, как коэффициенты разложения в кратный степенной ряд МакЛорена совместной характеристической функции

- центральные моменты

- многомерные кумулянты 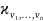(кумулянты - это коэффициенты в разложении логарифма характеристической функции случайной величины в ряд МакЛорена)

где

1. (18) Случайные процессы. Классификация. (Тихонов Харисов стр 54-57)

Случайный процесс описывает случайное изменение некоторой физической величины во времени. Описывается вероятностными законами. случайный процесс (СП) как функция изменения во времени. Аргументом СП является время.

Первый способ классификации:

В зависимости от того, скалярный или векторный сам процесс, его аргумент, можно ввести следующую классификацию:

1) скалярный случайный процесс случайный процесс, область значений которого есть множество в пространстве действительных чисел;

2) векторный случайный процесс случайный процесс, область значений которого есть множество в соответствующем координатном пространстве;

3) скалярное случайное поле случайный процесс, область значений которого есть множество из действительных чисел в соответствующем координатном пространстве;

4) векторное случайное поле случайный процесс, представимый в виде компонент, являющихся скалярными полями

Второй способ классификации.

В зависимости от того, непрерывное или дискретное множество, можно различать следующие основные виды случайных процессов:

1) дискретная случайная последовательность (дискретное время) – СП, у которого область определения – дискретные множества. В данном случае время t пробегает дискретный ряд значений, а случайная величина может принимать только дискретное множество значений. Множества значений могут быть как конечными, так и бесконечными

2) случайная последовательность – СП, у которого область значений - непрерывное множество, а область определения (время) - дискретное. Т.е. случайная величина может принимать бесконечное число значений.

3) дискретный случайный процесс (с непрерывным временем) – СП, у которого область значений – дискретное множество, а область определения - непрерывное множество. Т.е. может принимать только дискретные значения, а время t – континуум значений.

4) непрерывнозначный случайный процесс – СП, область значений и область определения которого – непрерывные множества. – континуум значений и аргумент t изменяется также непрерывно. При чём процесс может иметь разрывы первого рода (скачки).

Если скачки отсутствуют, то процесс называется непрерывным.

5 ) случайный точечный процесс (поток) представляет собой последовательность точек, случайным образом расположенных, на оси времени

.

2. (19) ПРВ случайного процесса, ее свойства. (Тихонов Харисов стр. 57-61)

Плотность распределения вероятности случайного процесса.

Если существует 2 случайных процесса , то можно записать их совместную n + m – мерные функции распределения и плотности вероятности так:

Если случайные процессы независимы друг от друга, то их совместная плотность распределения равна произведению плотностей.

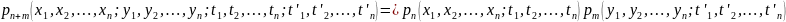
2 случайных процесса называются независимыми, если их совместную плотность можно представить в виде произведения плотностей. Если зависимы, то такое представление невозможно.

Плотность вероятности случайного процесса должна удовлетворять следующим условиям:

1) условию неотрицательности

2) условию нормировки

3) условию симметрии, то есть функции должны быть симметричны относительно любых перестановок аргументов

4) условию согласованности: при любом m < n

Последнее соотношение показывает, что из n-мерной плотности вероятностей всегда можно получить любую ПВ меньшей мерность путём интегрирования первой по «лишним» аргументам.

Условная плотность распределения вероятности характеризует случайное значение процесса при известном значении его в другой момент времени

Если процессы в момент времени независимы, то условная плотность вероятности не зависит от процессов во времени. Определяется только временем в данный момент.

Эта формула отражает необходимое и достаточное условие независимости случайных процессов в два момента времени.

3. (20) Моменты случайного процесса. (Тихонов Харисов стр 62-63)

Под начальными моментами функции случайного процесса принимают функции

………………………………………………………………

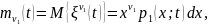
Такие моменты называются n-мерными моментами -го порядка

Вместо начальных можно рассматривать центральные моменты

Также моментные функции можно определить путём разложения характеристической функции в ряд Маклорена

где

Корреляционные и моментные функции связаны:

4. (21) Взаимосвязь между различными способами описания случайного процесса.

Связь плотности вероятности и характеристической функции через преобразование Фурье:

5. (22) Стационарные (в узком и широком смысле) и нестационарные случайные процессы. (Тихонов Харисов стр. 65-69) (в узк смысле – ф-ции распред вер инварианты отн времени, в широком – ковариац ф-ия и мат ожидание инвариантны отн времени)

Стационарный процесс в узком смысле – это процесс, в котором все конечномерные функции распределения вероятностей любого порядка инварианты* относительно сдвига по времени, то есть при любых n и t₀ справедливо равенство

*ИНВАРИАНТНОСТЬ — неизменность какой-либо величины при изменении физических условий или по отношению к некоторым преобразованиям

РЕАЛИЗАЦИЕЙ СЛУЧАЙНОГО ПРОЦЕССА X(t) называется неслучайная функция x(t), в которую превращается случайный процесс X{t} в результате опыта

Аналогичное равенство можно записать для плотности вероятности.

Это значит, что два процесса имеют одинаковые вероятностные характеристики при любом .

Процессы, которые не удовлетворяют этому условию называются нестационарными в узком смысле.

Понятие стационарности в узком смысле обобщается на два и несколько случайных процессов. Два случайных процесса называются совместно стационарно связанными в узком смысле, если их совместные функции распределения вероятностей любого порядка инвариан­тны относительно сдвига по времени:

Примечание. Если два процесса стационарны, то это не значит, что они будут стационарно связанными в узком смысле.

Пример.

n-мерная плотность вероятности, n-мерные моменты и корреляционные функции зависят не от n, а от (n-1) моментов времени, так как один из выбранных моментов времени можно всегда принять за начало отсчёта времени (например, положить )

Одномерная ПВ и одномерные моменты не учитывают временных характеристик, т.к.

*Функция является детерминированной, если для одного и того же набора входных значений она возвращает одинаковый результат.

Параметры стационарного в узком смысле случайного процесса:

• мат. ожидание

• взаимосвязь ковариационной и корреляционной функций

• дисперсия стационарного процесса постоянна и равна значению корреляционной функции при нулевом значении аргумента

Стационарные процессы в узком смысле:

• асимптотический стационарный процесс в узком смысле – стационарный процесс, при котором

• стационарный в узком смысле на конечном интервале – процесс, при котором равенство выполняется для всех временных точек этого интервала

• периодически стационарные или циклостационарные процессы в узком смысле с периодом Т – такие процессы, в которых равенство в предыдущем пункте выполняется только при

Стационарный в широком смысле процесс – это случайный процесс с конечной дисперсией, его мат. ожидание и ковариационная функция инвариантны относительно сдвига по времени

Два стационарных случайных процесса называются стационарно связанными в широком смысле, если их взаимная ковариационная функция инвариантна относительно сдвига по времени

Примечание. Как и для стационарных процессов в узком смысле имеет место быть утверждение, что если каждый из процессов является стационарным в широком смысле, то это не означает, что они являются связными в широком смысле.

6. (23) Эргодические и неэргодические случайные процессы. (Тихонов Харисов стр. 69-70)

До сих пор характеристики (плотностные вероятности, моментные функции) случайных процессов были определены через средние значения реализаций (функций) в ансамбле идентичных систем (систем с множеством реализаций, рассматриваемых в один момент времени, находящихся в одинаковых условиях | статистический ансамбль - это распределение вероятностей для состояния системы*).

*Источник https://wikiboard.ru/wiki/Statistical_ensemble_(mathematical_physics)

Для эргодических процессов данные характеристики можно получить путём осреднения соответствующих величин по одной реализации достаточно большой длительности.

Характеристики для эргодического случайного процесса:

• мат ожидание

• дисперсия

• корреляционная функция

На практике интервал осреднения T берут конечным, но большим

Если стационарный процесс протекает однородно (т.е. если поделить реализацию случайного процесса на части с равными промежутками и каждая часть будет представлять из себя отрезок реализации статистического ансамбля на выходе), то такой стационарный процесс обладает эргодическими свойствами.

Эргодическим в строгом смысле называется стационарный процесс, у которого с вероятностью единицы все его вероятностные характеристики могут быть получены из одной реализации процесса.

7. (24) Спектральное описание случайных процессов. Случайный спектр. (Тихонов Харисов стр. 80-82)

Если почти для всех реализаций спектра выполняется условие конечной мощности процесса, то такие процессы можно анализировать с помощью преобразования Фурье, т.е. для конкретной реализации процесса можно ввести спектральную функцию

где f – частота,

Для разных реализаций одного и того же случайного процесса спектральная функция 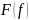тоже будет изменяться случайным образом, и поэтому её можно назвать случайным спектром.

Случайный спектр содержит всю информацию о конкретной реализации случайного процесса.

Характеристики случайного процесса в спектральной форме:

• мат. ожидание

• ковариационная функция . Заменяем ,

• спектральная плотность стационарного процесса

Случайный спектр F(f) является нестационарным процессом даже для стационарных случайных процессов

8. (25) Спектральная и взаимная спектральная плотность. (Тихонов Харисов стр. 82-88)

Спектральная плотность стационарного в широком смысле случайного процесса есть преобразование Фурье от ковариационной функции:

Основные свойства спектральной плотности:

1. Спектральная плотность стационарного процесса неотрицательная величина:

2. Спектральная плотность в широком смысле случайного процесса есть всегда вещественная функция, причём для вещественного процесса она является чётной функцией частоты.

Учитывая чётность спектральной функции и корреляционной функции запишем уравнения:

Таким образом спектральная плотность и корреляционная функция вещественного стационарного в широком смысле случайного процесса связаны между собой взаимным косинус-преобразованием Фурье

3. Т.к. корреляционная функция и спектральная плотность связаны между собой преобразованием Фурье, то чем «шире» спектр , тем «уже» корреляционная функция и наоборот.

Взаимная спектральная плотность

ВСП как и СП - это функция, зависящая от частоты.

Отличие ВСП от СП одного случайного процесса заключается в том, что ВСП двух стационарно связанных случайных процессов является комплексной функцией частоты.

Взаимная спектральная плотность двух случайных процессов есть прямое преобразование Фурье от взаимных ковариационных функций

9. (26) Гауссовские СП. БГШ. (Тихонов Харисов стр. 91-101)

Вещественный случайный процесс называется гауссовским, если для любого конечного множества моментов времени случайные величины имеют совместную нормальную (n-мерную) плотность вероятности: ,

где символ Т обозначает операцию транспонирования, - обратная матрица R, - определитель корреляционной матрицы

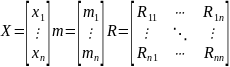
Для гауссовских процессов некоррелированность значений процесса тождественна их независимости, т.е. если , то

Условные плотности вероятностей значений совместно гауссовских процессов или значений одного гауссовского процесса являются нормальными. Этот результат следует из формулы:

При линейных преобразованиях гауссовсих случайных процессов свойство гауссовости сохраняется. Если на вход линейной системы с импульсной характеристикой h(t, τ) воздействует гауссовский случайный процесс , то при выполнении надлежащих условий интегрируемости процесс получившийся на выходе системы, будет также гауссовским. Справедливо и обратное утверждение: если каждый линейный функционал от есть гауссовская случайная величина 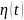, то является гауссовским случайным процессом.

Значимость гауссовских процессов этих процессов обусловлена тремя факторами:

1) многие реальные процессы в радиотехнике хорошо аппроксимируются именно гауссовскими процессами

2) в силу центральной предельной теоремы теории вероятностей сумма большого количества процессов с различными законами распределения может быть представлена гауссовскими случайными процессами

3) в случае различных преобразований негаусовских случайных процессов выходной процесс очень часто становится гауссовским.

Белый гауссовский шум.

Под БГШ n(t) понимается стационарный гауссовский случайный процесс с нулевым математическим ожиданием и дельтообразной корреляционной функцией:

Такой корреляционной функции соответствует спектральная плотность

10. (27) Постановка задачи оптимизации РТС.

Оптимизация (от латинского слова «optimus» – наилучший) – поиск наилучшего варианта, при наличии множества альтернативных. Для решения любой задачи необходимо формализовать объект оптимизации и представить его в виде математической модели.

Задача оптимизации заключается в следующем: требуется найти (если он существует), доставляющее экстремальное (минимальное или максимальное) значение целевой функции f(x) на множестве X , а именно для x₀ должно выполняться одно из условий:

либо

либо

Если такого элемента на множестве X не существует, то требуется построить последовательность

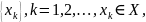
такую, что выполняется одно из соотношений

11. (28) Методы одномерной оптимизации. Методы прямого поиска.

В методе прямого поиска (нулевого порядка) для оптимизации целевой функции используются только значения самой функции, а значения её производных не используются.

Методы прямого поиска состоят из двух групп:

1) Пассивный. Все N точек , k = 1, …, N, в которых будут вычислены значения функции, выбирают заранее (до вычисления функции в этих точках);

2) Последовательный. Точки выбирают последовательно (для выбора последующей точки используют значения функции, вычисленные в предыдущих точках)

Будем считать, что стратегия поиска определена, если:

- определён алгоритм выбора точек

- определено условие прекращения поиска, т.е. условие, при выполнении которого значение f(x*) считают найденным с заданной точностью

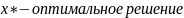
Оптимальный пассивный поиск состоит в выборе точек, равномерно расположенных на отрезке [a, b], координаты которых

При этом длина l_N интервала, содержащего минимум даёт оценку скорости сходимости пассивного поиска с ростом числа N точек, так как скорость сходимости любого метода прямого поиска можно характеризовать скоростью уменьшения интервала неопределённости с возрастанием N.

После определения координат точек находим значения функции в каждой из этих точек.

Найдём наименьшее значение функции f_j и, тогда точка оптимума и можно считать с точностью .

Методы последовательного поиска

В алгоритмах этих методов вычисляются значения функции в промежуточных точках интервала неопределённости:

Если , то в качестве границ нового интервала рассматривается интервал .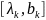

Если , это будет интервал [ ], если , то оставим интервал [ ]