Бодалев А.А., Столин В.В. - Общая психодиагностика (2000)-1

ная половина, в которую испытуемые зачисляются случайным образом -с помощью двоичной случайной последовательности(типа подбрасывания монетки и .т п.). В более общем случае такой простейший метод установления однородности двух эмпирических распределений может быть применен и при разбиении выборки по -ка кому-либо систематическому признаку. Если, в частности, по како- му-либо из популяционно значимых признаков(пол, возраст, образование, профессия) психолог получает значимую неоднородность эмпирических распределений; то это значит, что относительно данных популяционных категорий тестовые нормы должны быть специализированы (одна таблица норм - для мужчин, другая - для женщин и т. д.).

Более статистически корректный метод проверки однородности двух распределений, полученных при расщеплении выборки на равные части, опять же связан с применением критерия Колмогорова. Для этого с табличным значением сравнивается:

где Ке - эмпирическое значение статистики Колмогорова;

Fj1 - кумулятивная относительная частота для у-того интервала шкалы по первой половине выборки;

Fj2 - та же частота для второй половины; n - полный объем выборки.

Точные значения квантилей распределения Колмогорова для определения размеров выборки можно найти в кн.: Мюллер П. и др., 1982.

Применение критерия Колмогорова не зависит от нормальности целого распределения и от необходимости производить нормализацию интервалов.

* * *

Итак, априорная предпосылка нормальности распределения тестовых баллов основывается скорее на принципах операционального удобства, чем на теоретической необходимости. Психометрически корректные процедуры получения устойчивых тестовых норм возможны с помощью специальных методов непараметрической статистики (критерий «хи-квадрат» и т. п.) для распределений произвольной формы. Выбор статистической модели распределениязаконный произвол психометриста, пока сам тест выступает в качестве единственного эталона измеряемого свойства. В этом случае остается лишь тщательно следить за соответствием сферы применения диагностических норм той выборке испытуемых, на которой они были получены. Произвольность в выборе статистической модели

81

шкалы исчезает, когда речь заходит о внешних по отношению к тесту критериях.

Репрезентативность критериальных тестов. В таких тестах в качестве реального эталона применяется критерий, ради которого создается тест, - целевой критерий. Особое значение такой подход имеет в тех областях практики, где высокие результаты могут дать узкоспециализированные диагностические методики, нацеленные на очень конкретные и узкие критерии. Такая ситуация имеет место в обучении: тестирование, направленное на получение информации об уровне усвоения определенных знаний, умений и навыков(При профессиональном обучений), должно точно отражать уровень освоения этих навыков и тем самым давать надежный прогноз эффективности конкретной профессиональной деятельности, требующей применения этих навыков. Так возникают «тесты достижений», по отношению к которым критериальный подход обнаружил свою высокую эффективность (Гуревич К. М, Лубовский В. И,, 1982).

Рассмотрим операциональную схему шкалирования, применяемую при создании критериального теста. Пусть имеется некоторый критерий ,С ради прогнозирования которого психодиагност создает тест X. Для простоты представим С как дихотомическую переменную с двумя значениями: 1 и 0. С, = 1 означает, что j-й субъект достиг критерия (попал в «высокую» группу по критерию), Сj=0 означает, что i-й субъект не достиг критерия(попал в «низкую» группу). Психодиагност применяет на нормативной выборке тестX, и в результате каждый индивид получает тестовый баллXi. После того как для каждого индивида из выборки становится известным значение С (иногда на это требуются месяцы и годы после момента тестирования), психодиагност группирует индивидов по порядку возрастания балла Xi и для каждого деления исходной шкалы сырых тестовых баллов подсчитывает эмпирическую вероятность Р попадания в «высокую» группу по критерию С. На рис. 5 показаны распределения вероятности Р (Ci = 1) в зависимости от Xi

Рис. 5 Эмпирическая зависимость между вероятностью критериального события и тестовым баллом

Очевидно, что кривая на рис. 5 по своей конфигурации может совершенно не совпадать с кумулятивной кривой распределения

82

частот появления различныхXi. Кривая, представленная на рис. 5, является эмпирической линией регрессии С поXi Теперь можно сформулировать основное требование к критериальному тесту: линия регрессии должна быть монотонной функцией С отXi Иными словами, ни для одного более высокого значения X. вероятность Р не должна быть меньшей, чем для какого-либо менее высокого значения Xi Если это условие выполняется, то открывается возможность для критериального шкалирования сырых балловX. Так же как в случае с интервальной нормализацией», когда применяется поточечный перевод интервалов Х в интервалыZ, для которых выполняется нормальная модель распределения, так и при критериальном шкалировании к делениям сырой шкалыX применяется поточечный перевод прямо в шкалу Р на основании эмпирической линии регрессии. Например, если испытуемый А получил по тесту X 18 сырых баллов и этому результату соответствует Р=0,6, то испытуемому А ставится в соответствие показатель 60 %.

Конечно, любая эмпирическая кривая является лишь приближенной моделью той зависимости, которая могла бы быть воспроизведена на генеральной совокупности. Обычно предполагается, что на генеральной совокупности линия регрессии С по Х должна иметь более сглаженную форму. Поэтому обычно предпринимаются попытки аппроксимировать эмпирическую линию регрессии какойлибо функциональной зависимостью, что позволяет затем производить прогноз с применением формулы (а не таблицы или графика).

Например, если линия регрессии имеет вид приблизительно такой, какой изображен на рис. 6, то применение процентильной нормализации позволяет получить простую линейную регрессию С по нормализованной шкале Z. Это как раз тот случай, когда имеет место эквивалентность стратегии, использующей выборочностатистические тестовые нормы, и стратегии, использующей критериальные нормы.

Рис. 6. Зависимость вероятности критериального события Р от

нормально распределенного диагностического параметра X

83

Операции по анализу распределения тестовых баллов, построению тестовых норм и проверке их репрезентативности. Завершая этот раздел, кратко перечислим действия, которые последовательно должен произвести психолог при построении тестовых норм.

1.Сформировать выборку стандартизации(случайную или стратифицированную по какому-либо параметру) из той популяции, на которой предполагается применять тест. Провести на каждом испытуемом из выборки тест в сжатые сроки (чтобы устранить иррелевантный разброс, вызванный внешними событиями, происшедшими за время обследования).

2.Произвести группировку сырых баллов с учетом выбранного интервала квантования (интервала равнозначности). Интервал оп-

ределяется величиной W/m , где W=x max — х max; m - количество интервалов равнозначности (градаций шкалы).

3.Построить распределение частот тестовых баллов(для заданных интервалов равнозначности) в виде таблицы и в виде соответствующих графиков гистограммы и кумуляты.

4.Произвести расчет среднего арифметического значения и стандартного отклонения, а также асимметрии и эксцесса с помощью компьютера. Проверить гипотезы о значимости асимметрии и эксцесса. Сравнить результаты проверки с визуальным анализом кривых распределения.

5.Произвести проверку нормальности одного из распределений с помощью критерия Колмогорова(при n < 200 с помощью более мощных критериев) или произвести процентильную нормализацию с переводом в стандартную шкалу, а также линейную стандартизацию и сравнить их результаты(с точностью до целых значений стандартных баллов).

6.Если совпадения не будетнормальность отвергается; в этом случае произвести проверку устойчивости распределения расщеплением выборки на две случайные половины. При совпадении нормализованных баллов для половины и для целой выборки можно считать нормализованную шкалу устойчивой.

7.Проверить однородность распределения по отношению к варьированию заданного популяционного признака(пол, профессия

ит. п.) с помощью критерия Колмогорова. Построить в совмещенных координатах графики гистограммы и кумуляты для полной и частной выборок. При значимых различиях разбить выборку на разнородные подвыборки.

8.Построить таблицы процентильных и нормализованных тестовых норм (для каждого интервала равнозначности сырого балла). При наличии разнородных подвыборок для каждой из них должна быть своя таблица.

9.Определить критические точки (верхнюю и нижнюю) для

84

доверительных интервалов (на уровне Р < 0,01) с учетом стандартной ошибки в определении среднего значения.

10.Обсудить конфигурацию полученных распределений с учетом предполагаемого механизма выполнения того или иного теста.

11.В случае негативного результата: отсутствия устойчивых норм для шкалы с заданным числом градаций (с заданной точностью прогноза критериальной деятельности) - осуществить обследование более широкой выборки или отказаться от использования, данного теста.

3.2. НАДЕЖНОСТЬ ТЕСТА

В дифференциальной психометрике проблемы валидности и надежности тесно взаимосвязаны, тем не менее мы последуем традиции раздельного изложения методов проверки этих важнейших психометрических свойств теста.

Надежность и точность. Как уже отмечалось в разделе 3.1, общий разброс (дисперсию) результатов произведенных измерений можно представить как результат действия двух источников разнообразия: самого измеряемого свойства и нестабильности измерительной процедуры, обусловливающей наличие ошибки измерения. Это представление выражено в формуле, описывающей надежность теста и виде отношения истинной дисперсии к дисперсии эмпирически зарегистрированных баллов:

S 2

a = T (3.2.1)

Sx2

Так как истинная дисперсия и дисперсия ошибки связаны очевидным соотношением, формула (3.2.1) легко преобразуется в формулу Рюлона:

S2

a =1- e (3.2.2)

Sx2

где а - надежность теста; Se2 . -дисперсия ошибки.

Величина ошибки измерения - обратный индикатор точности измерения. Чем больше ошибка, тем шире диапазон неопределенности на шкале(доверительный интервал индивидуального балла), внутри которого оказывается статистически возможной локализация истинного балла данного испытуемого. Таким образом, для проверки гипотезы о значимости отличия балла испытуемого от среднего

85

значения оказывается недостаточным только оценить ошибку среднего, нужно еще оценить ошибку измерения, обусловливающую разброс в положении индивидуального балла (рис. 7).

Рис. 7. Соотношение распределений Sm – стандартное отклонение эмпирического среднего, St – стандартное отклонение ошибки

Как же определить ошибку измерения? На помощь приходят корреляционные методы, позволяющие определить точность (надежность) через устойчивость и согласованность результатов, получаемых как на уровне целого теста, так и на уровне отдельных его пунктов.

Надежность целого теста имеет две разновидности.

1. Надежность-устойчивость (ретестовая надежность). Измеряется с помощью повторного проведения теста на той же выборке испытуемых, обычно через две недели после первого тестирования. Для интервальных шкал подсчитывается хорошо известный коэффициент корреляции произведения моментов Пирсона:

åx12i x2i - åx1i åx2i

r12 = n

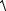(åx12i -(åx1i )2 / n)(åx22i -åx2i )2 / n)

где х1i. - тестовый балл i-го испытуемого при первом измере-

нии;

х2i. - тестовый балл того же испытуемого при повторном измерении;

n - количество испытуемых.

Оценка значимости этого коэффициента основывается на несколько иной логике, чем это обычно делается при проверке нулевой гипотезы - о равенстве корреляций нулю. Высокая надежность достигается тогда, когда дисперсия ошибки оказывается пренебрежительно малой. 'Относительную долю дисперсии ошибки легко определить по формуле

86

Таким образом, для нас существеннее близость к единице, а не отдаленность от нуля. Обычно в тестологической практике редко удается достичь коэффициентов, превышающих 0,8. При г = 0,75 относительная доля стандартной ошибки равна1 - 0,75 = 0,5 . Этой ошибкой, очевидно, нельзя пренебречь. При такой ошибке эмпирически полученное отклонение индивидуального тестового балла от среднего по выборке оказывается, как правило, завышенным. Для того чтобы выяснить «истинное» значение тестового балла индивида, применяется формула

хi — эмпирический балл i-го испытуемого;

r - эмпирически измеренная надежность теста; x - среднее для теста.

Предположим, испытуемый получил балл IQ по шкале Стэн- форда.-Бине, равный 120 нормализованным очкам, М = 100, г = 0,9.

Тогда истинный балл x¥ = 0,9 ´ 120 + 0,1 ´ 100 =118.

Конечно, требование ретестовой надежности является корректным лишь по отношению к таким психическим характеристикам индивидов, которые сами являются устойчивыми во времени. Если мы создаем тест для измерения эмоциональных состояний(бодрости, тревоги и т. д.), то, очевидно, требовать от него ретестовой надежности бессмысленно: у испытуемых быстрее изменится состояние, чем они забудут свои ответы по первому тестированию.

Для шкал порядка в качестве меры устойчивости к перетестированию используется коэффициент ранговой корреляции Спирмена:

где di — разность рангов /-го испытуемого в первом и втором ранговом ряду.

С помощью компьютера определяется более надежный коэффициент ранговой корреляции Кендалла (1975).

2. Надежностьсогласованность (одномоментная надежность). Эта разновидность надежности не зависит от устойчивости, имеет особую содержательную и операциональную природу. Простейшим способ ее измерения СОСТОИТЕ коррелировании параллельных форм теста (Анастази Д., 1982, кн. 1,с. 106). Чаще всего парал-

87

лельные формы теста получают расщеплением составного теста на «четную» и «нечетную» половины: к первой относятся четные пункты, ко второй - нечетные. По каждой половине рассчитываются суммарные баллы и между двумя рядами баллов по испытуемым определяются допустимые (с учетом уровня измерения) коэффициенты корреляции. Если параллельные тесты не нормализованы, то предпочтительнее использовать ранговую корреляцию. При таком расщеплении получается коэффициент, относящийся к половинам теста. Для того чтобы найти надежность целого теста пользуются формулой Спирмена - Брауна:

где rx - эмпирически рассчитанная корреляция для половин. Делить тест на две половины можно разными способами,

каждый раз получаются несколько разные коэффициенты(Аванесов В. С., 1982, с. 122), поэтому в психометрике существует способ оценки синхронной надежности, который соответствует разбиению теста на такое количество частей, сколько в нем отдельных пунктов. Такова формула Кронбаха:

где а - коэффициент Кронбаха; k- количество пунктов теста;

S 2j - дисперсия по j-му пункту теста;

Sx2 - дисперсия суммарных баллов по всему тесту.

Обратите внимание на структурное подобие формулы Кронбаха (3.2.2) и формулы Рюлона (3.2.8).

Несколько раньше была получена формула КьюдераРичардсона, аналогичная формуле Кронбаха для частного случаякогда ответы на каждый пункт теста интерпретируются как дихотомические переменные с двумя значениями (1 и 0):

88

где KR20 - традиционное обозначение получаемого коэффици-

ента;

p j q j -дисперсия i-и дихотомической переменной, какой являет-

ся

i-й пункт теста; р = N («верно») , q = 1 - p n

В 1957 г. Дж. Ките предложил следующий критерий для оценки статистической значимости коэффициента a:

степенью свободы;

k - количество пунктов теста; n - количество испытуемых;. a - надежность.

Формулы (3.2.8) и (3.2.9) позволяют оценить взаимную согласованность пунктов теста, используя при этом только подсчет дисперсий. Однако коэффициенты а и KR2I> позволяют оценить и среднюю корреляцию междуi-м и j-м произвольными пунктами теста, так как связаны с этой средней корреляцией следующей формулой:

Спирмена - Брауна, позволяющей прогнозировать повышения синхронной надежности теста с увеличением количества пунктов теста в k раз (Аванесов В. С., 1982, с. 121). Из этой формулы видно, что при больших k малое значение rij может сочетаться с высокой на-

дежностью. Пусть rij = 0,1, a k =100, тогда по формуле (3.2.11)

Широкое распространение компьютерных программ факторного анализа для исследования взаимоотношений между пунктами

89

теста (по одномоментным данным) привело к обоснованию еще одной достаточно эффективной формулы надежности теста, которой легко воспользоваться, получив стандартную распечатку компьютерных результатов факторного анализа по методу главных компонент:

теста;

k - количество пунктов теста;

λ1 - наибольшее значение характеристического корня матрицы интеркорреляций пунктов (наибольшее собственное значение,

или абсолютный вес первой главной компоненты).

Как и предыдущие формулы, формула (3.2.12) также относится к оценке надежности теста, направленного на измерение одной характеристики. Но, кроме того, она применима и для многофакторного теста, хотя и нуждается в пересчете после первоначального отбора пунктов, релевантных фактору (после того, как на основании многофакторного анализа отобраны пункты по одному фактору, снова проводится факторный анализтолько для этих отобранных пунктов).

Надежность отдельных пунктов теста. Надежность теста обеспечивается надежностью пунктов, из которых он состоит. Чтобы повысить ретестовую надежность теста в целом, надо отобрать из исходного набора пунктов, апробируемых в пилотажных психометрических экспериментах, такие пункты, на которые испытуемые дают устойчивые ответы. Для дихотомических пунктов (типа «решил - не решил», «да - нет») устойчивость удобно измерять с использованием четырехклеточной матрицы сопряженности:

Тест 1

Здесь в клеточке а суммируются ответы«Да», данные испытуемым при первом и втором тестировании, в клеточке b - число случаев, когда испытуемый при первом тестировании отвечал«Да», а при втором - «Нет» и т. д. В качестве меры корреляции вычисляется фи-коэффициент:

90