Задача 1. По каналу связи последовательно передано три знака. Описать пространство элементарных собы­тий и события:

1. принят только первый знак;

2. принят, по крайней мере, один знак;

3. приняты два и только два знака;

4. принято меньше двух знаков;

5. принят один знак

Решение. Используем цифры 0, 1 для обозначения собы­тий: 0 - знак искажен, 1 - знак принят. Тогда простран­ство элементарных событий запишется в виде

• Ω={000, 100,010,001, 110, 101,011, 111} и имеет раз­мерность восемь.

• Событие A₁ - принят только первый знак: A₁ = {100};

• Событие A₂ - принят по крайней мере один знак:

• A₂ = {100 + 010 + 001 + 110 + 101 + 011 + 111} = Ω\{000};

• Событие A3 - приняты два и только два знака: A₃ =

{110 + 011 + 101};

• Событие A₄ - принято меньше двух знаков: A₄ = {000 + 100 + 010 + 001};

• Событие A5 — принят один знак: A5 = {100 + 010 + 001}. Из полученных результатов следует, что

1. события A₁ и A₃ - несовместные

2. события A₄, A₃ - несовместные

3. события A₃, A₅ - несовместные

4. A₅ влечет A₄ (A₅ ⊂ A₄)

5. события A₁ и A₂ - совместны,

6. A₂ и A₃, A₁ и A₄, A₁ и A₅, A₂ и A₄ — совместные;

7. A₁ ⊂ A₅ ⊂ A₄ ; A₃ ⊂ A₂ ; A₁ = A₅ + A₂.

Изобразим эти события на схеме Эйлера-Венна.(1.5)

Задача 2 Игральная кость брошена дважды.

1. Описать пространство элементарных событий Ω.

2. Описать пространство элементарных событий, если его элементами служат суммы выпавших очков.

3. Назвать элементы Ω, составляющие события:

● A-суммаочковравна7;

● B - хотя бы на одной кости выпала 1;

● C - сумма очков делится на 3.

4. Описать словами события:

● D = {(11),(12),(21)};

● E = {(46), (55), (64)}.

5. Изобразить события A, B, C, D, E на диаграмме Эйлера-Венна.

Решение.

1. Ω = {11,12,13,14,15,16, 21, 22,..., 66},

2. Ω = {2,3,4,5,6, 7,8,9,10,11,12}

3. ● A = {16,61,34, 43, 25, 52};

● B = {11,12, 21,13,31,14, 41,15, 51,16, 61}

● C = {12, 21,36,63,45, 54,33,15, 51, 24,42,66}.

● D = {СУММА ОЧКОВ РАВНА 2 ИЛИ 3 };

● E = {СУММА ОЧКОВ РАВНА 10}.

Задача 3 Даны две электрические схемы: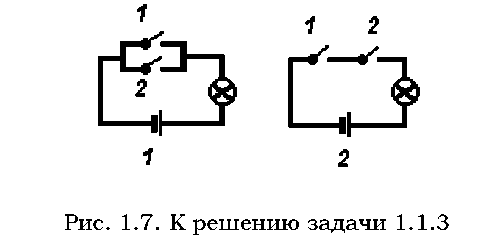

Описать событие: С = {ЦЕПЬ ЗAМКНУТA} для каждого случая.

Решение. Введем обозначения: событие A - контакт 1 за­мкнут; событие В - контакт 2 замкнут; событие С - цепь замкнута, лампочка горит.

1. Для параллельного соединения цепь замкнута, когда хотя бы один из контактов замкнут, поэтому С = A + В;

2. Для последовательного соединения цепь замкнута, ко­гда замкнуты оба контакта, поэтому С = A · В.

Задача. 1.1.4 Составлены две электрические схемы:

Событие A — цепь замкнута, событие A _i - i–й кон­такт замкнут. Для какой из них справедливо соотноше­ние

A₁ · (A₂ + A₃ · A₄) · A₅ = A?

Решение. Для первой схемы A = A₁ · (A₂ · A₃ + A₄ · A₅), так как параллельному соединению соответствует сумма собы­тий, а последовательному соединению — произведение событий. Для второй схемы A = A1 • (A₂ + A₃ • A₄ • A₅). Сле­довательно, данное соотношение справедливо для второй схемы.

Задача. 1.1.5 Упростить выражение (A + B)(B + C)(C+ A).

Решение. Воспользуемся свойствами операций сложения и умножения событий.

(A + B)(B + C)(A + C) =

(AB + AC + B B + BC)(A + C) =

= (AB + AC + B + BC)(A + C) =

(AB + AC + B)(A + C) = (B + AC)(A + C) =

= BA + BC + ACA + ACC = B A + BC + AC.

Задача. 1.1.6 Доказать, что события A,AB и A+B обра­зуют полную группу.

Решение. При решении задачи воспользуемся свойства­ми операций над событиями. В начале покажем, что эти события попарно несовместны.

A теперь покажем, что сумма этих событий дает простран­ство элементарных событий.

Задача. 1.1.7 С помощью схемы Эйлера–Венна проверить правило де-Моргана:

___ _ _

AB = A+B.

__

а) Заштриховано событие AB.

__ __

б) Событие A — вертикальная штриховка; событие B — горизонтальная штриховка. Событие

__ __

{A+B} — заштрихованная область.

Из сопоставления рисунков а) и в) следует:

___ _ _

AB = A+B.

Задача. 1.2.1 Сколькими способами можно рассадить 8 человек:

1. В один ряд?

2. За круглым столом?

Решение.

1. Искомое число способов равно числу перестановок из 8, т.е.

P₈ = 8! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 = 40320

2. Так как за круглым столом выбор первого человека не влияет на чередование элементов, то первым можно взять любого, а оставшихся упорядочим относительно выбранного. Это действие можно осуществить 8!/8 = 5040 способами.

Задача. 1.2.2 На курсе изучается 5 предметов. Скольки­ми способами можно составить расписание на субботу, ес­ли в этот день должны быть две различные пары?

Решение. Искомое число способов есть число размещений

из 5 по 2, так как нужно учесть порядок пар:

Задача. 1.2.3 Сколько экзаменационных комиссий, состо­ящих из 7 человек, можно составить из 15 преподавате­лей?

Решение. Искомое число комиссий (без учета порядка) — это число сочетаний из 15 по 7:

Задача. 1.2.4 Из корзины, содержащей двадцать прону­мерованных шаров выбирают на удачу 5 шаров. Опреде­лить число элементов пространства элементарных собы­тий этого опыта, если:

шары выбираются последовательно один за другим с возвращением после каждого извлечения;

шары выбирают один за другим, не возвращая;

выбирают сразу 5 шаров.