2. Граничные условия

В общем случае граничные условия имеют следующий вид:

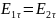; ; ; . Рассмотрим два наиболее важных частных случая:

I. Обе среды не проводят ток, т.е и .Тогда

; ; ; ;

; ; ;

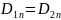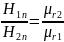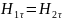
II. Вторая среда является идеальным проводником ( и соответственно, во второй среде отсутствует электромагнитное поле( ). Тогда получается:

; ; ;

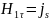
Вывод: На границе с идеальным проводником силовые линии электрического поля нормальны к этой границе, а силовые линии магнитного поля, напротив, касательны к ней.

Задача 1 Два диэлектрика разделяет бесконечная плоскость XoY. Параметры первого диэлектрика: , , .Параметры второго диэлектрика: , , .В первом диэлектрике на границе раздела задано электрическое поле:

, где , ,

Определить: Величину и направление вектора во второй среде.

Примем x за проекцию нормали, а z за проекцию касательной.

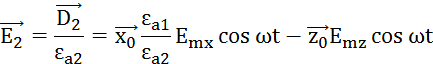
Задача 2

Два идеальных диэлектрика разделяет бесконечная плоскость YoZ.

Векторы напряженности электрического поля направлены под углами α₁=30° в первом диэлектрике и α₂=60° во втором относительно оси oX, нормальной границе раздела. Параметры первого диэлектрика: . Модуль вектора в первой среде E₁=0.1 В/м

Определить: диэлектрическую проницаемость второго диэлектрика, модуль вектора Е во второй среде, модули векторов электрического смещения в обеих средах вблизи границы

1.Определяем диэлектрическую проницаемость второго диэлектрика

,

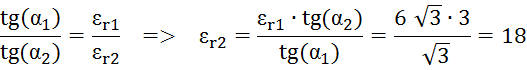
2.Определяем модуль вектора Е во второй среде

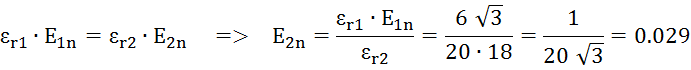
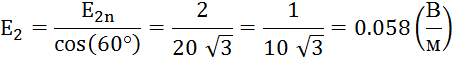
3.Определяем модули векторов электрического смещения в обеих средах вблизи границы

Задача 3

Прямоугольная площадка, выполненная из идеального металла, расположена в плоскости XoY. Площадка имеет размеры 10см х 37см и окружена идеальным диэлектриком с параметрами . Вблизи площадки задана напряженность магнитного поля А/м.

Определить величину и направление поверхностного тока j_s на площадке, пренебрегая краевым эффектом.

Определить величину и направление вектора магнитной индукции B вблизи площадки.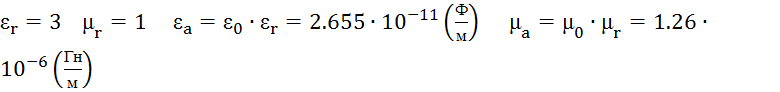 1.Определям величину и направление поверхностного тока j_s на площадке, пренебрегая краевым эффектом.

[А / м²] направлен по оси х

2.Определям величину и направление вектора магнитной индукции B вблизи площадки.

3. Энергия электромагнитного поля

3.1 Уравнение баланса мгновенных значений мощностей

Электромагнитное поле – это особая форма существования материи. Энергия электромагнитного поля, в зависимости от характера порождающих его источников, может либо быть локализованной в определенной области пространства, либо перемещаться в пространстве, при этом она также может преобразовываться в другие виды энергии, например в тепловую.

Баланс энергии электромагнитного поля в некотором объеме V, ограниченном замкнутой поверхностью S, определяется теоремой Умова-Пойнтинга в интегральной форме для мгновенных значений мощностей

(3.1)

или, используя физический смысл каждого слагаемого в (1.3),

(3.2)

где энергия, запасаемая в электрическом поле W ^эл и магнитном поле W ^маг

(3.3)

а мощность излучения, входящая или выходящая через S

где вектор Пойнтинга,

мощность тепловых потерь

, (3.4)

мощность сторонних источников

(3.5)

В большинстве практических задач уравнение баланса упрощается. Например, еcли в V нет сторонних источников, то j^ст = 0 и Р^ст = 0, если среда в V не проводит электрический ток Ϭ = 0, то J=0 и Р^пот = 0. и т.д.

Следует отметить. что все подынтегральные выражения в (3.1) являются соответствующими плотностями мощности или энергии т.е. это мощности или энергия отнесенные к 1м³ .Например, мгновенная объемная плотность энергии, запасаемая в электрическом или магнитном полях вычисляется по формуле

(3.6)

Отметим, что все интегралы в (3.1) , кроме интеграла характеризующего тепловые потери, могут принимать положительные или отрицательные значения, что соответствует разным физическим явлениям, например, если > 0, то мощность от стороннего источника передается электромагнитному полю, если < 0, то энергия , запасенная в поле передается потребителю, и т.д.

3.2 Активная, реактивная и комплексная мощности.

Как известно из курса «Теория электрических цепей», если в электрической цепи напряжение U и ток I изменяются во времени по гармоническому закону, то мгновенное значение мощности P в цепи, определенное по закону Джоуля – Ленца, может быть представлено в виде двух слагаемых , где – называют активной мощностью, среднее значение которой за период , а –называют реактивной мощностью, которая изменяется во времени по гармоническому закону с удвоенной частотой и амплитудой _мах , среднее значение которой за период . В этом случае . Тогда вводят понятие комплексная мощность , где – коплексная амплитуда U, а – комплексно сопряженная амплитуда I. При этом

. (3.7)

Аналогично, можно ввести комплексные мощности в любом другом случае: для этого нужно первый сомножитель в выражении для мгновенных значений мощности заменить соответствующей ему комплексной амплитудой, а второй –комплексно- сопряженной амплитудой соответствующей ему и результат умножить на 1/2.

Например, мощности, входящие в (3.1):

1. комплексная мощность сторонних источников ,

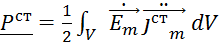в этом случае , а

;

2. комплексная мощность джоулевских потерь

, а

3. комплексный вектор Пойнтинга

(3.8)

в этом случае

; (3.9)

при этом

(3.10)

4. комплексная энергия . запасаемая в электрическом и магнитном полях

в этом случае и

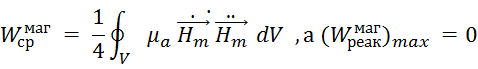
Средняя объемная плотность энергии, запасаемая в электрическом или магнитном полях вычисляется по формуле

, (3.11)