Цель практикума

Методические указания призваны помочь в организации всех видов внеаудиторной, индивидуальной работы; их можно использовать при изучении электродинамических дисциплин с целью получения знаний, умений, навыков решения задач без участия преподавателя и для реализации различных видов контроля знаний. Методические указания содержат задачи по разделам первой части курса “Электромагнитные поля и волны”: Уравнения Максвелла. Параметры сред. Граничные условия. Баланс мощностей в объеме. Плоские электромагнитные волны. Задачи составлены так, что не требуют привлечения большого объема знаний и значительных затрат времени на вычисления. Результаты оформляются в виде рефератов по указанным разделам согласно рабочей программе по курсу “Электромагнитные поля и волны”.

1.Уравнения Максвелла. Параметры сред. Краткие теоретические сведения

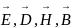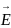В современной технике связи работу многих технических устройств высокочастотного диапазона невозможно оценить без привлечения аппарата электромагнитных волн. Если говорят, что в некоторой области пространства известна структура электромагнитного поля, то это означает, что в каждой точке этого пространства известны следующие четыре вектора . Вектор характеризует напряженность электрического поля и служит мерой интенсивности (силы) этого поля в данной точк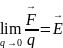е: , где - сила, действующая на неподвижный малый заряд .Амплитуда вектора напряженности электрического поля измеряется в вольтах на метр [В/м]. Амплитуда вектора электрической индукции измеряется в кулон на метр квадратный [Кл/м²]. , ,где -абсолютная диэлектрическая проницаемость среды, 8.85 диэлектрическая проницаемость вакуума,

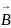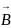Вектор магнитной индукции характеризует силовое воздействие магнитного поля на движущийся положительный заряд: ,где - скорость движения заряда. Амплитуда вектора магнитной индукции измеряется в веберах на метр квадратный [Вб/м²]. , .

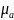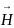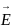Где: - абсолютная магнитная проницаемость вещества (среды), -магнитная проницаемость вакуума, -относительная магнитная проницаемость вещества. Вектор называется вектором напряженности магнитного поля. Амплитуда вектора напряженности магнитного поля измеряется в амперах на метр [А/м]. Векторы и описывают электрическое поле, векторы и описывают магнитное поле. Помимо основных векторов теория электромагнетизма оперирует с рядом вспомогательных величин, описывающих свойства заряженных частиц.

1.Заряд Q может быть произвольно распределен внутри поверхности S. Поэтому в общем случае , где  – объемная плотность зарядов; V – объем, ограниченный поверхностью S, в котором сосредоточены заряженные частицы. Объемная плотность зарядов где Q – заряд, сосредоточенный в объем V. Размерность  – кулон на кубический метр (Кл/м³). Единица измерения Q – кулон [Кл]. Заряд может быть определен через поверхностную плотность зарядов, [Кл/м²]

2.Удельная проводимость среды = ,где R – сопротивление воображаемого цилиндра длиной и площадью поперечного сечения , заполненного данной средой. Удельная проводимость среды измеряется в сименс на метр [См/м]. Величина плотности тока проводимости связана с величиной вектора напряженности электрического поля следующим уравнением (закон Ома в дифференциальной форме) . Уравнение получило название закон Ома в дифференциальной форме.

3.Плотность тока проводимости = , где -единичный вектор, показывающий направление тока (направление движения положительных зарядов) в рассматриваемой точке М, - плоская площадка, содержащая точку М, расположенная перпендикулярно вектору , ток проводимости, протекающий через . Амплитуда плотности тока проводимости измеряется в ампер на метр квадратный [А/м²]. Плотность тока связана с током следующим уравнением 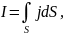Поверхностный ток, протекающий в тонком поверхностном слое, определяется через поверхностную плотность тока 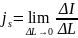[А / м]. Ток смещения выражается через плотность тока смещения j^см соотношением 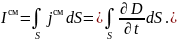где: j^см = D/t

Ток проводимости и ток смещения в вакууме имеют различную физическую сущность. Ток проводимости – это упорядоченное движение свободных электрических зарядов. Ток смещения в вакууме соответствует только изменению электрического поля и не сопровождается каким-либо движением электрических зарядов.

Проводники и диэлектрики

Среды могут сильно отличаться друг от друга по величине удельной проводимости, поэтому электромагнитные поля в таких средах могут обладать разными свойствами. Чем больше величина , тем больше плотность ока проводимости в среде при той же напряженности электрического поля. Часто для упрощения анализа вводят понятия идеального проводника и идеального диэлектрика. Идеальный проводник – это среда с бесконечно большой удельной проводимостью (), а идеальный диэлектрик – среда, не обладающая проводимостью ( = 0). В идеальном проводнике может существовать только ток проводимости, а в идеальном диэлектрике – только ток смещения. В реальных средах имеется как ток проводимости, так и ток смещения. Поэтому проводниками принято называть среды, в которых ток проводимости намного превосходит ток смещения, а диэлектриками – среды, в которых основным является ток смещения. Такое деление сред на проводники и диэлектрики имеет относительный характер, так как существенно зависит от скорости изменения электромагнитного поля.В случае монохроматического поля комплексные амплитуды векторов плотности тока проводимости и плотности тока смещения равны соответственно Отношение является критерием деления сред на проводники и диэлектрики. Если tg ≫1 среду называют проводником, если tg ≪1 – диэлектриком. Из соотношения следует, что диэлектрические свойства сильнее проявляются при более высоких частотах. Существует ряд сред, занимающих промежуточное положение между проводниками и диэлектриками, Такие среды (их называют полупроводящими) на одних частотах являются проводниками (≫), а на других – диэлектриками (≪).