

3. СОГЛАСОВАННЫЙ ФИЛЬТР.
3.1. Параметры и характеристики согласованного фильтра. Оптимальный фильтр - это фильтр, обеспечивающий на выходе
максимальное отношение мощности сигнала к мощности шума. Если помеха,
поражающая сигнал, является белым шумом, то оптимальный фильтр называется - согласованным фильтром (СФ). Таким образом, если на вход
СФ поступает сигнал uc(t) в сумме с белым шумом x(t): z(t)=uc(t)+x(t),
то на выходе СФ получим максимальное отношение мощности сигнала к мощности шума. Определим, какими должны быть характеристики СФ. Напряжение на выходе линейного фильтра с импульсной реакцией g(t) имеет вид:
|
t |
|
|
|
t |
|
|
|
|
uвых (t) = ∫uc (τ )g(t −τ )dτ + ∫ x(τ )g(t −τ )dτ ; |
|||||||
0 |
|
|
|
0 |
|
|
(3.1) |
|
Первое слагаемое – |
напряжение полезного сигнала, второе – напряжение |
|||||||
помехи. Дисперсия помехи равна: |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
t |
2 |
|
|
|
|
|
|
|
|
t |
t |
|
|
= |
||
σ 2 = ∫ x(τ )g(t − τ )dτ |
= ∫ x(τ )g(t −τ )dτ ∫ x(v)g(t − v)dv |
|||||||
|
0 |
|
|
0 |
0 |
|
|
|
t t |
|
|
t |
t |
|
|
|
|
= ∫ ∫ x(τ )x(v) g(t −τ )g(t − v)dτ dv = ∫ ∫G0δ (τ − v) g(t −τ )g(t − v)dτ dv =
0 0 0 0
t
= G0 ∫ g 2 (t − τ )dτ ;
0
(3.2)
где G0δ(τ-ν) – функция корреляции белого шума со спектральной плотностью энергии G0.
Отношение мощности сигнала к дисперсии шума на выходе СФ равно:
99

|
|
|
t |
|
|
2 |
|
t |
t |
|
t |
|
|
|
|
|
|
|
|
||||||
|
|
∫ u c |
(τ )g(t − τ )dτ |
|
|
∫ uc2 (τ )dτ ∫ g 2 (t − τ )dτ |
|
∫ uc2 (τ )dτ |
|
|||
h 2 = |
|
0 |
|
|
|
≤ |
0 |
0 |
≤ |
0 |
; |
|
|
|
t |
|
|
t |
G0 |
||||||
|
|
|
G0 ∫ g 2 (t − τ )dτ |
|
|
|
G0 ∫ g 2 (t − τ )dτ |
|
|
|||
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
h2 ≤ |
|
∫ uc2 (τ )dτ |
|
|
|
|
|
|
|
|||
0 |
|
|
; |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
G0 |
|
|
|
|
|
|
(3.3) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Первое неравенство записано в соответствии с неравенством Буняковского – Шварца. Замена t на Т во втором неравенстве выполнена, исходя из неотрицательности подинтегрального выражения, которое не убывает при увеличении верхнего предела. Равенство в (3.3) достигается только при условии, что
g(t)=uc(T-t); |
(3.4) |
Это означает, что название фильтра "согласованный" определяется тем, что его характеристики согласованы с характеристиками сигнала uс(t):
- импульсная реакция g(t) согласованного фильтра совпадает с зеркальным отображением сигнала:
g(t)=uс(Т-t) |
(3.5) |
Для импульса несимметричной формы, заданного, например, выражением: uc(t) = Um(l-t/T), при 0 < t < T,
импульсная реакция фильтра, согласованного с |
ним, равна: |
|
g1(t)=u(T-t)=Umt/T, |
при |
0 < t < T. |
Соответствующий треугольный сигнальный импульс и импульсная реакция согласованного с ним фильтра имеют вид рис.3.1а,б.
а) |
б) |
Рис.3.1.
Определим частотную характеристику СФ, как преобразование Фурье от g(t):
100

T |
T |
|
K( jω) = ∫g(t)e− jωtdt =∫uc (T −t)e− jωtdt = |
|
|
0 |
0 |
|
T |
|
|
= e− jωT ∫uc (z)ejωzdz =e− jωT Sc (− jω) =| Sc (− jω)| e− j[ωT+ϕ(ω)]; |
(3.6) |
|
0 |
|
|
Таким образом, амплитудно-частотная характеристика (АЧХ) согласованного фильтра |К(jω)| с точностью до постоянного множителя A совпадает с
амплитудным спектром сигнала |S(jω)|: |
|
|К(jω)|=A|S(jω)| |
(3.7) |
- фазо-частотная характеристика (ФЧХ) согласованного фильтра |
|
противоположна по знаку ФЧХ сигнала: |
|
φ(ω)= - φс( ω) – ωТ; |
(3.8) |
Рассмотрим характеристики фильтра, согласованного с одиночным прямоугольным импульсом (рис.3.2). Такой импульс описывается выражением:
u(t)=Um, при -0,5Т < t < 0,5Т ;
где Um,T - амплитуда и длительность импульса, соответственно.
Рис.3.2.
Спектр этого импульса равен:
S(j ω)=UmTsin(ω T/2)/( ω T/2). (3.9)
Следовательно, АЧХ фильтра, согласованного с прямоугольным импульсом равна:
|K(jω )|=UmT |
|
sin(ωТ/2) |
|
; |
A=1 |
(3.10) |
|
( ω T/2) |
|||||||
|
|
|
|||||
|
|
|
|
|
|||
На рис.3.3 нарисована АЧХ фильтра, согласованного с прямоугольным импульсом длительностью Т.
101
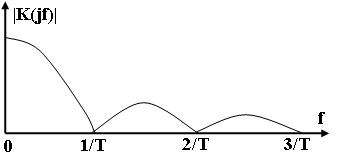
Рис.3.3.
Согласованный фильтр обеспечивает на выходе максимальное отношение мощности сигнала к мощности шума (с/ш), если помеха является белым шумом. Выше было показано, что для помехи типа АБГШ отношение мощности сигнала к мощности шума на выходе СФ при оптимальном выборе
характеристик СФ равно |
отношению энергии посылки сигнала к |
спектральной плотности энергии белого шума: |
|
h02 = Ес /G0 |
(3.11) |
Это максимальное отношение, которое может быть получено для помехи типа белый шум.
На базе СФ можно построить оптимальный приемник. Если передаются двоичные сигналы U1(t) и U0(t), то оптимальный приемник содержит два фильтра: СФ1, согласованный с сигналом Ul(t), и СФ0, согласованный с
сигналом U0(t). |
|
|
Сигналы U1(t), U0(t) - это импульсы длительностью |
Т, форма которых |
|
зависит от вида модуляции: |
|
|
ДАМ: U1(t)=Um cos ω0t ; |
U0=0; |
|
ДЧМ: U1(t)=Um cos ω1t; |
U0(t)=Um cos ω0t ; |
(3.12) |
ДФМ: U1(t)=Um cos ω0t ; |
U0(t)= - Um cosω0t ; |
|
Оптимальный приемник двоичных сигналов на согласованных фильтрах показан на рис.3.4.
 Рис.3.4.
Рис.3.4.
Если напряжение V1на выходе СФ1 больше, чем V0, то решение приемника - "1", если V1 < V0, то решение приемника - "0" .
Выражения (3.12) позволяют сделать вывод, что оптимальный приемник сигналов ДАМ и ДФМ должен содержать только один СФ с АЧХ, равной:
102
|
|
|
U mТ |
|
sin |
(ω − ω0 )Т |
|
|
|||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
| K(jω ) |= |
|
|
|
2 |
|
|
|
|
|||||
2 (ω − ω0 )Т |
|||||||||||||
|
|
|
|
|
|||||||||
|
|
|
2 |
|
|
|
(3.13) |
||||||
|
|
||||||||||||
Оптимальный приемник сигналов ДЧМ должен содержать два СФ:
|
|
|
U mТ sin |
(ω − ω1 )Т |
|
|
|
|||||||||
|
|
|
|
|
||||||||||||
Сф1 с АЧХ, равной: |
| K1 (jω ) |= |
|
|
2 |
|
|
|
|
|
|||||||
|
2 |
|
|
|
(ω − ω1 )Т |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
U mТ sin |
(ω − ω0 ) |
|
Т |
|
||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
СФ0 с АЧХ, равной: |
| K 0 |
(jω ) |= |
2 |
|
|
|
|
|
||||||||
2 |
|
|
|
|
(ω − ω0 )Т |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
(3.14)
(3.15)
Потенциальная помехоустойчивость такого приемника совпадает с помехоустойчивостью оптимального приемника.
3.2. Шумоподобные сигналы (Ш П С).
Одна из трудноразрешимых проблем при разработке новых систем связи – проблема нахождения оптимальных систем сигналов, реализующих максимальные скорость передачи и помехоустойчивость приема. Для
многолучевых каналов мобильной связи устойчивую связь можно получить, в частности, используя сложные, шумоподобные сигналы. К таким
сигналам относятся М-последовательности, коды Баркера, функции Уолша и
т.п. Сложные или шумоподобные сигналы называют также
псевдослучайными последовательностями (ПСП). Псевдослучайная последовательность - это последовательность 1 и -1, которые генерируются по определенным известным правилам, но внешне напоминают реализацию шума. По этой причине такие последовательноси называются также
шумоподобными. |
Для ПСП характерно также, что их база В, т.е. |
|
произведение длительности сигнала Т на ширину его спектра F значительно |
||
больше 1: |
|
|
|
B=FT>> 1. |
(3.16) |
Поэтому ПСП называют также сигналами |
с большой базой. ПСП |
|
выбирают так, чтобы их автокорреляционная функция имела явно выраженный максимум, а взаимокорреляционная функция была близка к нулю.
Рассмотрим свойства М-последовательностей, которые являются разновидностью линейных рекуррентных последовательностей (ЛРП).
Двоичные линейные рекуррентные |
последовательности |
– |
это |
|
последовательности двоичных символов {аi}={a1,a2,…..a |
i}, удовлетворяющих |
|||
рекуррентному правилу: |
|
|
|
|
с0аi =с1аi+1Å с2аi+2 Åс3аi+3Å с4аi+4Å …. |
Åсkаi+k ; |
сi=0 или 1; |
|
(3.17) |
Устройство, генерирующее ЛРП состоит из элементов памяти и сумматоров по модулю 2. Эти операции делает регистр сдвига с обратными
103
связями. ЛРП задаётся производящей функцией G(x), под которой понимают формальный степенной ряд :
Ґ |
|
G(x) = ∑ аi хi |
(3.18) |
i = 0 |
|
mod2 |
|
где аi - символы последовательности; |
хi - определяет место символа |
в последовательности (i=0 – первый символ слева).
Например : 10110= а0 х0 Å а1 х1 Å а2 х2 Å а3 х3 Å а4 х4=1 Å х2 Å х3 ;
так как: а0 =1 ; а1=0 ; а2 =1 ; а3 =1; а4=0 .
Производящую функцию можно представить в виде:
G(x) = |
g(x) |
; |
(3.19) |
|
|||
|
f(x) |
|
|
g(x) – многочлен степени r<k; |
|
||
k |
|
||
f(x) = ∑ сi хi - характеристическое уравнение |
или характеристический |
||
i=1 |
|
||
mod2 |
|
||
многочлен Степень ЛРП равна памяти регистра сдвига. Задаваясь разными многочленами g(x) и f (x), можно получить разные ЛРП. Например, пусть g(x)=1,
f (x)= 1 Å х2 Å х5. В результате деления g(x) на f(x) получим последовательность: 1010110101….., т.е. некоторую ЛРП.
Каждому характеристическому многочлену степени k соответствует некоторое множество последовательностей с периодом Ni , определяющим циклическую структуру данной последовательности. Если период ЛРП равен N=2k -1, то такие последовательности называются последовательностями максимального периода или М – последовательностями. Если данная ЛРП
является М-последовательностью, то её характеристический многочлен f(x) - неприводимый многочлен, т.е. его нельзя разложить на произведение двух
или более многочленов. Существуют таблицы неприводимых многочленов разных степеней. Например, существует 4 двоичных многочлена 2-ой степени, из которых:
-(х)2 =(х)(х) - приводимый;
-х2 Å1=(хÅ1)(х Å1) – приводимый,
т.к. (хÅ1)(х Å1) =( х2 Åх Åх Å1)= х2 Å1; при выполнении умножения
следует помнить, что х Åх=0;
-х2 Åх =х(хÅ1) – приводимый;
-х2 ÅxÅ1 – неприводимый.
Структурные свойства М – последовательностей:
1.Период М – последовательности равен N=2k –1, где k – степень характеристического многочлена.
2.М – последовательности имеют максимальный период среди ЛРП с равными степенями характеристического многочлена.
3. В М – последовательности порядка k содержатся все кодовые комбинации из k символов, кроме комбинации из одних нулей, причем каждая комбинация встречается только один раз. Например, М –
104
последовательность порядка k=3 имеет вид:001011100101110010111….. Её период N = 23 –1 =7 и содержит последовательность 0010111. Последовательность из 18 импульсов содержит все возможные комбинации из 3-х импульсов 001,011,100,101,110,010,111.
4.В одном периоде М – последовательности порядка k содержится 2k-1 «единиц» и (2k-1–1) « нулей».
5.Корреляционные свойства М – последовательностей.
Наиболее общей характеристикой корреляционных свойств М – последовательностей является взаимная функция неопределенности
(ВФН) Rjk(τ,Ω):
|
|
2Е ∫ |
|
|
|
|
R jk (τ, Ω) = |
1 |
∞ Аj |
(t)А*k (t - τ) еjΩtdt; |
(3.20) |
|
|
||||
|
|
|
-∞ |
|
|
Е – |
энергия М – последовательностей; |
|
|||
A(t)j |
, Ak*(t) – j- я и |
k-я |
М – последовательности (звёздочка означает |
||
комплексно сопряженную функцию). |
|
||||
Сечение ВНФ при Ω=0 дает взаимную корреляционную функцию Rjk(τ). Если j=k , то выражение (3.20) даёт функцию неопределённости ФН. При
j=k и Ω=0 получим из (3.20) нормированную автокорреляционную функцию, связанную преобразованием Винера-Хинчина с энергетическим
спектром М – |
последовательности G(ω): |
|
||||||
R(τ) = |
1 |
∞ |
Аj |
(t) А*j (t - τ) dt = |
1 ∞ |
G(ω) ejωtdω; |
(3.21) |
|
|
|
|
||||||
|
4πЕ ∫ |
|||||||
|
2Е ∫ |
|
|
|
|
|||
|
|
-∞ |
|
|
|
-∞ |
|
|
Если М – последовательность периодически повторяется с временным периодом Tп=NТ, где Т- длительность одного импульса, то автокорреляционная функция периодической М – последовательности (ПАКФ) равна:
|
|
|
|
|
|
|
τ |
|
1 |
|
1 |
NT |
|
|
[1 - |
|
(1 + |
|
)]; | τ |< T; |
||
|
|
Т |
N |
|||||||
R(τ) = |
|
∫0 |
аi |
(t)аi |
(t - τ)dt = |
1 |
|
|
|
|
NT |
|
|
|
|
||||||
|
|
|
|
|
Т≤ τ ≤ (N - 1)T; |
|||||
|
|
|
|
|
- |
|
; |
|||
|
|
|
|
|
N |
|||||
|
|
|
|
|
|
|
|
(3.22) |
||
|
|
|
|
|
|
|
|
|
||
На рис.3.5 показана стандартная ПАКФ М – последовательности. Нормированная ПАКФ:
-имеет максимум, равный 1;
-является периодической с периодом NT;
-длительность (ширина) пика ПАКФ равна Т;
-боковые лепестки постоянны и равны -1/N.
Взаимная ПКФ зависит от выбора М-последовательностей. Проблема состоит в том, чтобы подобрать достаточное количество М- последовательностей , для которых взаимная ПКФ не превышает заданной
105

величины. Для хороших М-последовательностей уровень боковых лепестков имеет величину N-0.5.
R(τ)
1
τ
 NТ
NТ 
Рис.3.5.
М-последовательности формируются регистром сдвига, который представляет собой генератор двоичных последовательностей. Он содержит триггерные ячейки (элементы памяти) и сумматоры по модулю 2,
охваченные обратными связями.
Регистр сдвига является цифровым автоматом, работа которого описывается характеристическим полиномом f(x) степени k. Этот
полином, как указано выше, является:
-неприводимым ;
-примитивным (первообразным), т.е. на него делится без остатка полином
степени (1+хN) при N=(2k –1) и на него не делится без остатка полином
(1+хL) при L<N.
Количество ячеек регистра равно степени характеристического полинома k. Если коэффициент аi =1, то выход i-ой ячейки подключен к сумматору по модулю 2, если коэффициент аi =0, то выход i-ой ячейки не подключен к сумматору по модулю 2. На рис.3.6 приведена схема регистра сдвига, описываемого характеристическим полиномом f(x)= 1 Å х2 Å х3. Для него k=3 (3 ячейки) и выходы 2-ой и 3-ей ячеек подключены к сумматору по модулю 2.
|
1 |
|
|
|
|
|
|
|
ВЫХОД |
|
|
2 |
|
|
|
3 |
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.3.6.
Пусть регистр находится в состоянии 100, т.е. в 1-ой ячейке записана ‘1’,
во 2-ой и в 3-ей ячейках записан ‘0’. |
Тактовые |
импульсы сдвигают |
||
импульсы, записанные в ячейках «вправо». Так как |
во 2-ой и 3-ей ячейках |
|||
записаны нули, то на выходе сумматора тоже ‘0’ |
и ‘0’ записывается в 1-ю |
|||
ячейку. Из 1-ой ячейки ‘1’ записывается во 2-ю, |
а ‘0’ из 2-ой записывается |
|||
в 3-ю. Из 3-ей ячейки “0” идет на выход. |
Регистр перешел в состояние 010. |
|||
Теперь на выходе сумматора |
1+0=1. Следующий такт : ‘1’ из сумматора |
|||
записывается в 1-ю ячейку, ‘0’ |
из 1-ой ячейки записывается во 2-ю, ‘1’ из 2- |
|||
106
ой ячейки записывается в 3-ю, ‘0’ из 3-ей ячейки идет на выход и т.д. В результате на выходе получаем М-последовательность: 0010111001011100101110010111…..
У неё период N=23-1=7 импульсов, в периоде 22-1=3 нуля и 22=4 единицы. Проблема состоит в том, чтобы получить достаточно большое количество М-последовательностей с достаточно малыми взаимно-корреляционными функциями. Количество М-последовательностей равно Q = ϕ(N)/k ,
где ϕ(N) – функция Эйлера, т.е. количество чисел в ряду от 1 до (N-1) взаимно простых с N . Если N – простое число, то ϕ(N)= N-1.
Для k=3, N=7, ϕ(7)=6, Q=2. Для k=19, Q=27594.
Одним из типов ПСП являются коды Баркера. Это сравнительно короткие ПСП длиной 3, 5, 7, 11, 13 импульсов. На рис. 3.7 показана временная диаграмма кода Баркера с N=11: +1 +1 +1 -1 -1 -1 +1 -1 -1 +1 -1. На рис.3.8
показана его автокорреляционная функция.
 Рис. 3.7.
Рис. 3.7.
 Рис.3.8.
Рис.3.8.
Сильной стороной этих кодов является то, что боковые лепестки автокорреляционных функций имеют уровень 1/N.
3.3.Фильтры, согласованные с шумоподобными сигналами.
107

Согласованные фильтры обычно используются для оптимального приема шумоподобных сигналов (ШПС). Аналоговый фильтр, согласованный с ШПС содержит:
1.Линию задержки с отводами; количество отводов равно количеству импульсов, время движения импульса от одного до другого отвода равно длительности импульса;
2.Фазовращатели (+,-); фазовращатель со знаком "+" не меняет, а со знаком "-" меняет знак входного импульса на противоположный; чередование знаков фазовращателей совпадает с зеркальным отображением чередования знаков в сигнале.
3.Сумматор; 4.Фильтр согласованный с одиночным прямоугольным импульсом (ФСОИ).
На рис.3.9 нарисована структурная схема фильтра, согласованного с кодом Баркера из 11-ти импульсов:+1+1+1-1-1-1+1-1-1+1-1. Этот СФ имеет линию задержки с 11-ю отводами, фазовращатели, сумматор и ФСОИ.
Чередование знаков фазовращателей в СФ: "- + - - + - - - + + +" , совпадает с зеркальным отображением чередования знаков в сигнале.
Рис.3.9.
На рис.3.10 изображена временная диаграмма напряжения u1(t) на выходе сумматора фильтра, согласованного с 11-значным кодом Баркера, при подаче на его вход согласованного с ним сигнала (толстая линия).
108
